Chapter I
- 1. BY: MARIA FERNANDA VERGARA M. UNIVERSIDAD INDUSTRIAL DE SANTANDER
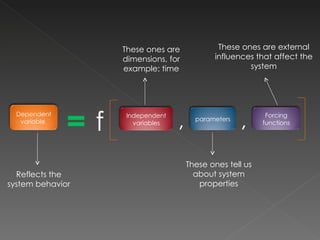
- 2. A mathematical model is a description of a physical phenomenon , process, even an economic system, using a mathematical formulation or equation. It can be seen as a functional relationship, taking into account itâs parameters: f , , Dependent variable Independent variables parameters Forcing functions
- 3. f , , Reflects the system behavior These ones are dimensions, for example: time These ones tell us about system properties These ones are external influences that affect the system Dependent variable Independent variables parameters Forcing functions
- 4. To formulate a mathematical model you will need to follow the next steps:
- 5. Express the hypotesis in terms of differential equations Solving the D.E. Showing model predictions If required, raise the complexity of the model or change the hypothesis Hypothesis Testing Getting solutions Mathematical formulation or equation
- 6. W F r Newtonâs Second Law: Where: a is the dependent parameter F is the forcing function m is the parameter ÂŋWhich is the terminal velocity of a free-falling body near the earthâs surface?
- 7. W F r Net Force: F r + W Fr = -c v W= mg Where and Drag Coefficient Solving, and taking into account that initial velocity is 0: Analytical or exact solution
- 8. An analytical solution satisfies the differential equation, but there are many mathematical models that cannot be solved exactly, here is when we need numerical methods to solve the equation and get an aproximated solution. This way we can solve the problem of the parachute getting a numerical solution:
- 9. Source: CHAPRA,Steven C., Numerical Methods for Engineers. Mc Graw Hill Using Newtons law, but realizing that the time rate of change of velocity can be aproximated by: We can get a numerical solution for the same problem of the parachute:
- 10. Now we got a numerical solution for the problem of the parachute, so if you have an initial time and velocity for some time t i , you can easily get the velocity at a time t i+1 . This velocity at the time t i+1 can be used to extend the computation to the velocity at t i+2 and so on.
- 11. CHAPRA, Steven C. Numerical Methods for engineers. Mc Graw Hill. ZILL, Dennis. Differential Equations with modeling applications. International Thomson Publishing Company.