Chord at une-presentation
Download as PPT, PDF
0 likes192 views
This document describes using Hidden Markov Models to determine hidden chord parameters from observable melody bars of music. It calculates transition and observation probabilities from expert knowledge on music and 250 lead sheets. The Viterbi algorithm is then used to find the most likely chord sequence given the melody notes by maximizing the probability of chords given the melody notes. Target users include general and intermediate users who would get chord analysis, and technical experts and professionals who could also evaluate the performance and technology.
Chord at une-presentation
- 11. HMM can modeled to determine hidden parameters from the observable data.
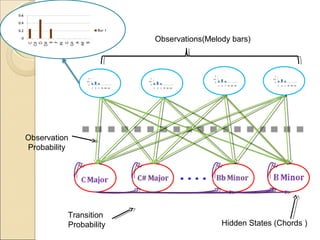
- 14. Observations(Melody bars) Observation Probability Transition Probability Hidden States (Chords )
- 15. 250 Lead Sheets Expert Knowledge on Music Calculate Aij=P (Chord i / Chord i-1) B Observation Probability matrix A Transition Probability Ai,j = 留Amaji,j X (1-留) Amini,j Matrix 留- Emotional Factor Bij=P (MelodyBar / Chord) . Di,j D Pitch Class Vector = P(StartChord/Chord)
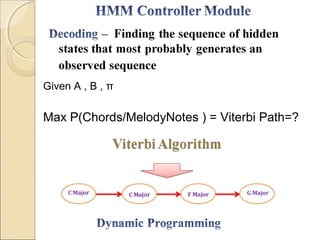
- 16. Given A , B , Max P(Chords/MelodyNotes ) = Viterbi Path=?
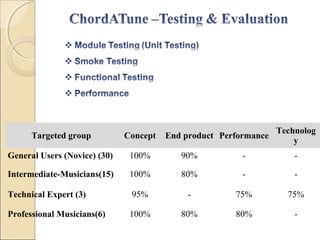
- 17. Technolog Targeted group Concept End product Performance y General Users (Novice) (30) 100% 90% - - Intermediate-Musicians(15) 100% 80% - - Technical Expert (3) 95% - 75% 75% Professional Musicians(6) 100% 80% 80% -
Editor's Notes
- This explains the problem domain/novelty and the solution
- Write the basic requirement input/process/output
- Funtionalities of ChordATune from the basic requirements Significant feature that was incorporated was da emotions
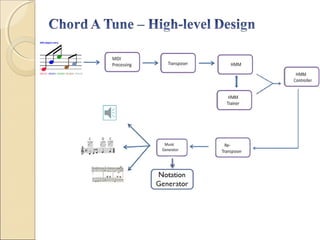
- Desig + Process of ChordATune
- Technology (this is brief)
- How the input is handled
- Core Module HMM Module
- How HMM parameters are mapped to the project
- How HMM parameters are mapped to the project
- Algorithms
- Testing -