�ݺ�ߣ

TOPIC : COIN CHANGING
(DP & GREEDY)
WELCOME TO THE PRESENTATION

THINGS TO BE EXPLAINED:
? DP & Greedy
? Definition Of Coin Changing
? Example with explanation
? Time complexity
? Difference between DP & Greedy in Coin
Change Problem

DP : DYNAMIC PROGRAMMING
? Dynamic programming is a method for solving a complex
problem by breaking it down into a collection of simpler sub
problems just once and storing their solutions.
? DP is used to solve problems with the following characteristics :
?Simple Sub problems
?Optimal Structure Of The Problems
?Overlapping Sub problems

GREEDY ALGORITHM
?A greedy algorithm always makes the choice that looks best
at the moment. It makes a locally optimal choice in the hope
that this choice will lead to a globally optimal solution.
?An algorithm is greedy if it builds a solution in small steps,
choosing a decision at each step locally , not considering what
happen ahead to optimize some underlying criterion

COIN CHANGE PROBLEM
Coin change is the problem of finding the minimum number
of ways of making changes for a particular amount of taka,
using a given unlimited amounts of coins. It is a general case
of Integer Partition.

D[1] = C[P �C D[1]] + 1; here D[1] = 1;
= C[6 �C 1 ] +1;
= C[5] +1 ;
= 5 +1;
= 6
MINIMUM
NUMBER
OF COINS
EXAMPLE:
Set Of Coins, D = { 1,5,6,9 }
Make Change Of Taka, n = 11
0 1 2 3 4 1 1 2 3 1 2 3
1 1 1 1 5 6 1 1 9 5
C[P] =
S[P] =
0 1 2 3 4 5 6 7 8 9 10 11 P
5
2
50 6
For P=6;
D[2] = C[P �C D[1]] + 1; here D[2] = 5;
= C[6 �C 5 ] +1;
= C[1] +1 ;
= 1+1;
= 2
D[3] = C[P �C D[1]] + 1; here D[3] = 6;
= C[6 �C 6] +1;
= C[0] +1 ;
= 0 +1;
= 1
0, if P = 0
min ( C[P-D[i]] + 1 ), if P > 0
D[1] <= D[i] <=P
C[P] =

EXPLANATION OF COIN CHANGE (DP) :
C[P] =
TIME COMPLEXITY:
Time Complexity = O(m*n), where m = Total taka & n = Number of coin
? If D is unsorted , then sort D in Ascending Order
? Take two array C[P] and S[P] where,
C[P] = Minimum number of coins used for P Tk
S[P] = Last coin used to make P Tk.
? Fill the C[P] and S[P] tables
? Find C[P] using the following equation,
0, if P = 0
min ( C[P-D[i]] + 1 ), if P > 0
D[1] <= D[i] <=P

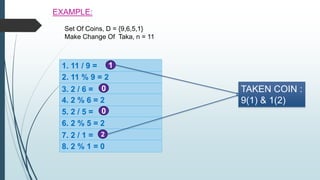
EXAMPLE:
Set Of Coins, D = {9,6,5,1}
Make Change Of Taka, n = 11
3. 2 / 6 =
2. 11 % 9 = 2
1. 11 / 9 =
5. 2 / 5 =
4. 2 % 6 = 2
6. 2 % 5 = 2
7. 2 / 1 =
8. 2 % 1 = 0
1
0
0
2
TAKEN COIN :
9(1) & 1(2)

? If D is unsorted, then sort D in descending order.
? Find the taken coin and their minimum number using the following algorithm
for(D[1] to D[n] )
{
result = n/D[i];
n = n (mod) D[i];
if(result = 0)
print result and D[i]
}
? Repeat for each coin
EXPLANATION OF COIN CHANGE (GREEDY):
TIME COMPLEXITY:
Time complexity = O(n), where n = Number of coin

? Set Of Coins, D = {1,5,6,9}
? Make Change Of Taka, n = 11
o Result :
Minimum Number of coin : 2.
The coins : 5, 6.
? Set Of Coins, D = {1,5,8,10}
o Result :
The coins : 10, 5.
? Set Of Coins, D = {9,6,5,1}
o Result :
The coins : 9(1), 1(2).
? Set Of Coins, D = {10,8,5,1}
o Result :
The coins : 10(1), 5(1).

�ݺ�ߣ

Coin change Problem (DP & GREEDY)

More Related Content

Coin change Problem (DP & GREEDY)