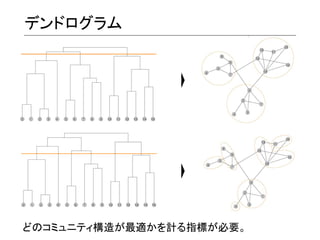
Community detection
- 1. Community Detection -? Girvan Newman Algorithm -? Newman Algorithm
- 2. Community Detectionって? あるネットワークの中で、 ? 密にリンクされたノードの集まりを見つける。 ? コミュニティ間は疎 コミュニティ内は密
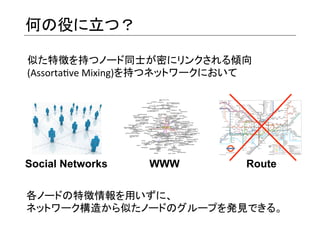
- 3. 何の役に立つ? 似た特徴を持つノード同士が密にリンクされる傾向 ? (Assorta)ve ?Mixing)を持つネットワークにおいて ? Social Networks WWW Route 各ノードの特徴情報を用いずに、 ? ネットワーク構造から似たノードのグループを発見できる。 ?
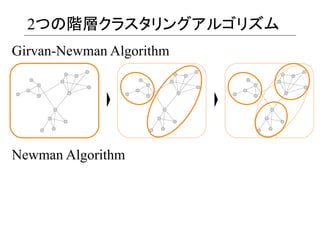
- 4. 2つの階層クラスタリングアルゴリズム Girvan-Newman Algorithm Newman, ?M.E.J., ?Girvan, ?M., ?2004. ?Finding ?and ?evalua)ng ?community ?structure ?in ?networks. ? ? Physical ?Review ?E, ?69(2), ?026113. ? ? Newman Algorithm Newman, ?M.E.J., ?2004. ?Fast ?algorithm ?for ?detec)ng ?community ?structure ?in ?networks. ? Physical ?Review ?E, ?69(6), ?066133. ? ?
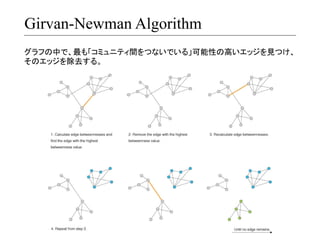
- 9. コミュニティ間をつなぐエッジ、どう見つける? Shortest-?‐path ?betweenness ? 同一コミュニティ内の二点間の最短経路はほとんど重複しないはず。 ? 別々のコミュニティに属する二点間の最短経路の ? 多くが同じエッジを通過するはず。 ?
- 12. Modularity Q N Q = ∑ (eii ? a ) 2 i i=1 N (-?‐1/2<=Q<=1) ? : コミュニティ数 ? eii : 総エッジ数に対する ? 両端がコミュニティ i ?に含まれるエッジの割合 ? ai : 総エッジ数に対する ? 少なくとも片端がコミュニティ i ?に含まれるエッジの割合 ?
- 13. Modularity Qの意味 N Q = ∑ (eii ? a ) 2 i i=1 -?‐? 「コミュニティ内のエッジ数が多い」だけでは不十分。 ? -?‐? それだと全ノードが同じコミュニティに属している場合が最大。 ? -?‐? ランダムグラフにおけるコミュニティ内エッジ数の期待値と比較。 ?
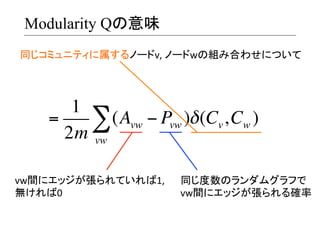
- 14. Modularity Qの意味 同じコミュニティに属するノードv, ?ノードwの組み合わせについて ? 1 = ∑(Avw ? Pvw )δ (Cv, Cw ) 2m vw vw間にエッジが張られていれば1, ? ? 無ければ0 ? 同じ度数のランダムグラフで ? vw間にエッジが張られる確率 ?
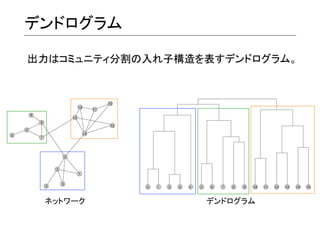
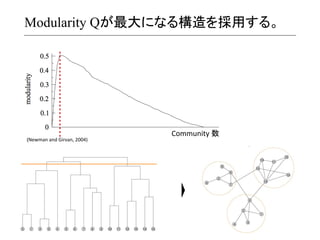
- 15. Modularity Qが最大になる構造を採用する。 (Newman ?and ?Girvan, ?2004) ? Community ?数 ?
- 16. Girvan-Newman Algorithmの欠点 計算量が非常に大きい。 ? -?‐? 消去するエッジを見つけるための ? ?betweennessの計算がO(mn) ? ? -?‐? 全エッジを消去するためm回繰り返すので ? ?合計O((m^2)n) ?
- 17. Newman Algorithm
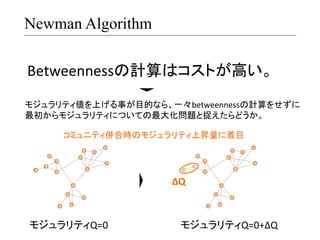
- 18. Newman Algorithm Betweennessの計算はコストが高い。 ? モジュラリティ値を上げる事が目的なら、一々betweennessの計算をせずに ? 最初からモジュラリティについての最大化問題と捉えたらどうか。 ? コミュニティ併合時のモジュラリティ上昇量に着目 ? ΔQ ? モジュラリティQ=0 ? モジュラリティQ=0+ΔQ ?
- 19. コミュニティ合併時のモジュラリティ上昇量に着目 合併時のモジュラリティ上昇が大きい ? 合併してもモジュラリティ上昇は少ない ? ΔQij = Qnew ? (Qi + Q j ) = eij + e ji ? 2ai a j = 2(eij + ai a j )
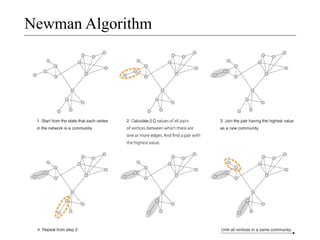
- 20. Newman Algorithm
- 21. Newman Algorithmの計算量 ? -?‐? コミュニティの併合とΔQの再計算にO(m+n) ? -?‐? 全ノードが一つのコミュニティになるまで繰り返す ? ?ので、全体としてO((m+n)n) ? -?‐ ? 後にデータ構造を工夫したCNMアルゴリズムに ?よってO(n ?log^2n)まで小さくなった。 ? ?
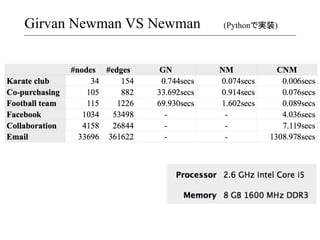
- 22. Girvan Newman VS Newman 精度はほとんど同じか、Girvan-?‐Newmanの方が少し良い程度。 ?
- 23. Girvan Newman VS Newman (Pythonで実装)
- 24. まとめ Girvan-?‐Newman ?Algorithm ? -?‐? トップダウンでコミュニティを分割していく ? -?‐? Shortest-?‐path ?betweennessに基づいてエッジを消去 ? -?‐? O((m^2)n) ? Newman ?Algorithm ? -?‐? ボトムアップでコミュニティを併合していく ? -?‐? モジュラリティの最大化が目的 ? -?‐? コミュニティ併合時のモジュラリティ上昇に着目 ? -?‐? O((m+n)n) ?
- 25. References -?‐ ?Girvan-?‐Newman ?Algorithm ? Newman, ?M.E.J., ?Girvan, ?M., ?2004. ?Finding ?and ?evalua)ng ?community ?structure ?in ?networks. ? ? Physical ?Review ?E, ?69(2), ?026113. ? ? (hZp://arxiv.org/abs/cond-?‐mat/0308217) ? -?‐ ?Newman ?Algorithm ? Newman, ?M.E.J., ?2004. ?Fast ?algorithm ?for ?detec)ng ?community ?structure ?in ?networks. ? ? Physical ?Review ?E, ?69(6), ?066133. ? (hZp://arxiv.org/abs/cond-?‐mat/0309508) ? ? -?‐ ?CNM ?Algorithm ? Clauset, ?A., ?Newman, ?M.E.J., ?Moore, ?C., ?2004. ?Finding ?community ?structure ?in ?very ?large ?networks. ? ? Physical ?Review ?E, ?70(6), ?066111. ? ? (hZp://arxiv.org/abs/condmat/0408187) ? -?‐ ?各種コミュニティ発見アルゴリズムの比較 ? Lancichine`, ?A., ?Fortunato, ?S., ?2009. ?Community ?detec)on ?algorithms: ?a ?compara)ve ?analysis. ? ? Physical ?Review ?E, ?80(5), ?056117. ? (hZp://arxiv.org/abs/0908.1062) ? ?