Comparison Singular and Non-singular
?
0 likes?1,445 views
A non-singular matrix is invertible, has independent columns and rows, and has a unique solution to equations of the form Ax=b. A singular matrix is not invertible, has dependent columns and rows, and the equation Ax=b may have no solution or multiple solutions. Key differences between singular and non-singular matrices include whether the determinant is zero, the number of solutions to Ax=0, the matrix rank, and whether eigenvalues can be zero.
Comparison Singular and Non-singular
- 1. Singular and Non-singular Matrix Yuji Oyamada 1 HVRL, Keio University 2 Chair for Computer Aided Medical Procedure (CAMP), Technische Universit：t M：nchen a u April 10, 2012
- 2. Non-Singular A is non-singular means that A is invertible (A?1 exists). Can solve Ax = b as ? = A?1 b. x The above solution is unique. For homogeneous system Ax = 0, the only solution is x = 0. Y. Oyamada (Keio Univ. and TUM) Singular and Non-singular Matrix April 10, 2012 2/4
- 3. Singular A is singular means that A is not invertible (A?1 doet not exist). Either a solution to Ax = b does not exist, there is more than one solution (not unique). The homogeneous system Ax = 0 has more than one solution. In?nitely many non-trivial solutions. Y. Oyamada (Keio Univ. and TUM) Singular and Non-singular Matrix April 10, 2012 3/4
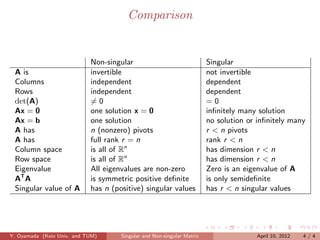
- 4. Comparison Non-singular Singular A is invertible not invertible Columns independent dependent Rows independent dependent det(A) =0 =0 Ax = 0 one solution x = 0 in?nitely many solution Ax = b one solution no solution or in?nitely many A has n (nonzero) pivots r < n pivots A has full rank r = n rank r < n Column space is all of Rn has dimension r < n Row space is all of Rn has dimension r < n Eigenvalue All eigenvalues are non-zero Zero is an eigenvalue of A AT A is symmetric positive de?nite is only semide?nite Singular value of A has n (positive) singular values has r < n singular values Y. Oyamada (Keio Univ. and TUM) Singular and Non-singular Matrix April 10, 2012 4/4