Computer Graphics - Lecture 02 transformation
- 1. Transformation Computer Graphics 4052 6 October Dr Anton Gerdelan gerdela@scss.tcd.ie
- 2. Simplest Example ŌŚÅ Easiest way to scale our triangle? ŌŚÅ Easiest way to move our triangle? ŌŚÅ Demo time
- 3. First ŌĆō Maths Revision ŌŚÅ Q. Define a ŌĆō 3d point ŌĆō 3d vector ŌĆō 3d unit vector ŌŚÅ Q. What do we use each for in graphics?
- 4. Modify from Main Programme? ŌŚÅ How can we update/change the amount that we move or scale? ŌŚÅ Hint: use a shader keyword ŌŚÅ Demo time
- 5. Rotation ŌŚÅ Q. How can we rotate our triangle? ŌŚÅ How can we rotate a 3d point? ŌŚÅ Rotation is around the origin (the 0,0,0 point)
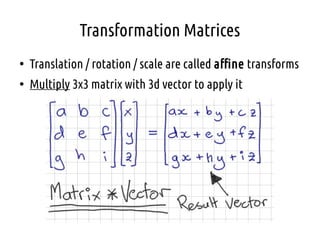
- 6. Transformation Matrices ŌŚÅ Translation / rotation / scale are called affine transforms ŌŚÅ Multiply 3x3 matrix with 3d vector to apply it
- 7. Matrix * Vector ŌŚÅ Q. What is the result in the vector? ŌŚÅ i.e. what does this matrix do?
- 8. Row-Major vs. Column-Major ŌŚÅ We will use column-major notation ŌŚÅ Multiplication order for column-major is right-to-left ŌŚÅ It is possible to use row-major instead (most DX apps do) Reversed in row-major Column
- 9. 3X3 Rotation Around Z-Axis cos(theta) -sin(theta) 0.0 sin(theta) cos(theta) 0.0 0.0 0.0 1.0 ŌŚÅ Theta will be in radians in C ŌŚÅ Right-hand rule for rotation direction ŌŚÅ Q. Which way will my triangle turn on screen?
- 10. Rotation Demo ŌŚÅ Define matrix as an array of floats (how many for a 3x3?) ŌŚÅ Array memory is in column order for OpenGL ŌŚÅ Update shader uniform for matrix inside main loop ŌŚÅ glUniform...() family of functions ŌŚÅ glUniformMatrix3fv() takes an array of 9 floats
- 12. 4x4 Homogenous Matrices ŌŚÅ You can use 3d matrices, but we tend to use 4d matrices in graphics, and 4d vectors/points. ŌŚÅ These are not 4d hyper-geometry - it's a sneaky exploit. ŌŚÅ Q. Any idea why we might like 4d matrices?
- 13. Matrix * Vector Rules ŌŚÅ A 3x3 matrix (mat3) can only multiply with a 3d vector (vec3) ŌŚÅ A 4x4 matrix (mat4) can only multiply with a 4d (vec4) ŌŚÅ Q. If we have a 4x4 matrix and a 3d point, how do we make our 3d point into a 4d point?
- 14. 4d Vectors ŌŚÅ XYZ and W ŌŚÅ vec4 in GLSL ŌŚÅ For POINTS set the 4th component to 1.0 ŌŚÅ For VECTORS set the 4th component to 0.0 ŌŚÅ Q. Any idea why? ŌŚÅ vec4 (1.0, 5.0, -20.0, 0.0); ŌŚÅ vec4 (0.0, -1.0, 0.0, 1.0); This is a dirty trick!
- 15. Now, What Was the Point in Going 4d? ŌŚÅ We can combine many matrices together by multiplication ŌĆō mat4 M = R * T * S; ŌĆō vec4 result = M * vec4 (vp.xyz, 1.0); ŌŚÅ Send fewer matrix uniforms updated over the bus ŌŚÅ Create a transformation pipeline (more on that soon)
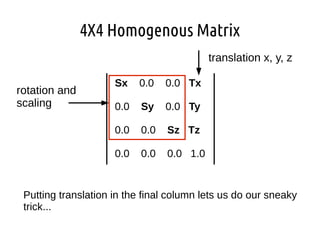
- 16. 4X4 Homogenous Matrix Sx 0.0 0.0 Tx 0.0 Sy 0.0 Ty 0.0 0.0 Sz Tz 0.0 0.0 0.0 1.0 rotation and scaling translation x, y, z Putting translation in the final column lets us do our sneaky trick...
- 17. Matrix * Vector ŌŚÅ Q. Can you figure it out? What the 0 or 1 does at the end of a vec4?
- 18. Matrix * Vector ŌŚÅ Q. Can you figure it out? What the 0 or 1 does at the end of a vec4?
- 19. Matrix Multiplication a b c d e f g h AB = = (ae + bg) (af + bh) (ce + dg) (cf + dh) Each cell in result is = Sum of: A(our row, first col) * B(first row, our col) + ... ... ... + A(our row, last col) * B(last row, our col) A B
- 20. Identity Matrix 1.0 0.0 0.0 0.0 0.0 1.0 0.0 0.0 0.0 0.0 1.0 0.0 0.0 0.0 0.0 1.0 Main diagonal
- 21. Transpose Matrix ŌŚÅ Swaps between column-major and row-major layout ŌŚÅ Flip values over the main diagonal ŌŚÅ Q. Can y'all compute the transpose of this? 1.0 0.5 0.0 0.0 0.0 2.0 0.0 0.0 -5.0 0.0 1.0 -1.0 0.0 0.0 0.0 1.0
- 22. Inverse Matrix ŌŚÅ Reverses any matrix transformation ŌŚÅ Or transform relative to another object ŌŚÅ Quite complicated to compute ŌŚÅ Work out determinant, then multiply with cofactors 1.0 0.0 0.0 2.0 0.0 1.0 0.0 0.0 0.0 0.0 1.0 0.0 0.0 0.0 0.0 1.0 Q. Guess?
- 23. Most Important Homework 1.Find out how to build & use the following for 4x4 matrices on paper: ŌĆō Identity ŌĆō Scaling ŌĆō Translation ŌĆō Rotation around X axis, Y axis, and Z axis ŌĆō Matrix * Matrix 2.Spot the difference between row and column-major layouts ŌĆō Hint: column-major has the translation in part in a column 3.Know which order multiplication goes in R-to-L or L-to-R?
- 24. Guidelines ŌŚÅ Get a 3d maths library for C/C++ or make your own ŌĆō Christophe Riccio's GLM http://glm.g-truc.net/ ŌĆō I made a simple one (Blackboard) ŌŚÅ Make a cheat-sheet (or grab mine off Blackboard) ŌŚÅ Know how the maths work for all of these operations ŌŚÅ If unusure ŌĆō textbooks and online sources! ŌŚÅ This stuff definitely comes up in job interview tests, especially certain famous companies starting with 'H'
- 25. Next ŌŚÅ Extending the transformation pipeline to add a virtual camera ŌĆō viewing position and angle ŌĆō using perspective
- 26. Notes ŌŚÅ I deliberately skipped some things ŌĆō Vector addition ŌĆō Unit vectors and normalisation ŌĆō Dot product of 2 vectors ŌĆō Cross product of 2 vectors ŌŚÅ I plan to introduce this where we actually use it (lighting) ŌŚÅ ...and because I ramble too much