�ݺ�ߣ

Computing Full Disjunctions Yaron Kanza Yehoshua Sagiv The Selim and Rachel Benin School of Engineering and Computer Science The Hebrew University of Jerusalem

A Formal Definitions of Full Disjunction

Preliminary Notations Given a set of relations r 1 , …, r n with schemes R 1 , …, R n , respectively We denote with t ij the j -th tuple of r i For X  R i , we denote by t ij [ X ] the projection of t ij on X Next, we give some preliminary definitions

Scheme Graph Two distinct schemes R i and R j are connected if R i  R j is non-empty The scheme graph of R 1 , …, R n consists of A node for each scheme R i An edge between R i and R j if R i and R j are connected Movies Actors Actors-that-Directed Acted-in

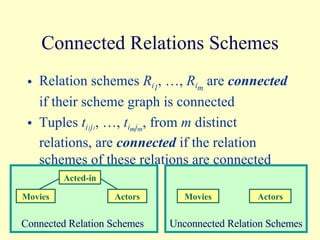
Connected Relations Schemes Relation schemes R i 1 , …, R i m are connected if their scheme graph is connected Tuples t i 1 j 1 , …, t i m j m , from m distinct relations, are connected if the relation schemes of these relations are connected Movies Actors Acted-in Connected Relation Schemes Movies Actors Unconnected Relation Schemes

Join Consistent Tuples Two tuples t i 1 j 1 and t i 2 j 2 are join consistent if t i 1 j 1 [ R i 1  R i 2 ] = t i 2 j 2 [ R i 1  R i 2 ] m tuples, from m distinct relations, are join consistent if every pair of connected tuples are join consistent

Universal Tuple A universal tuple u is defined over all the attributes in R 1  …  R n and consists of null and non-null values We denote by û the non-null portion of u A universal tuple is called integrated tuple if there are m connected and join consistent tuples t i 1 j 1 , …, t i m j m such that û is the natural join of t i 1 j 1 , …, t i m j m

Maximal Universal Tuple A universal tuple u subsumes a universal tuple v if u is equal to v on all the non-null attributes of v (i.e., u can be created from v by replacing some null values with non-null values) In a given set D , a tuple u is maximal if there is no tuple in D , other than u , that subsumes u

A Full Disjunction The full disjunction of r 1 , …, r n i s the set of all maximal integrated tuples that can be generated from m tuples of r 1 , …, r n

Acyclic Scheme Given a set of schemes R 1 , …, R n , their scheme hypergraph consists of A node for each attribute that appears in some R i For each R i (1  i  n ), a hyperedge that includes the attributes of R i α- acyclic scheme hypergraph: All the hyperedges can be removed by a sequence of ear removals γ- acyclic scheme hypergraph: The Bachman diagram of the scheme hypergraph is acyclic

Product Graph Given a query Q and a database D , the product of Q and D is a graph such that The nodes are pairs of a node of Q and a node of D The edges are between nodes such that the pair of nodes of Q and the pair of nodes of D both are connected by edges with the same label in Q and in D , respectively The root is the pair of the root of Q and the root of D

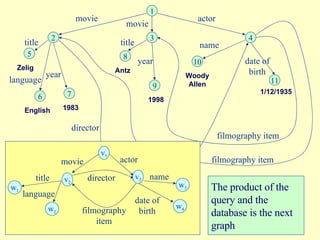
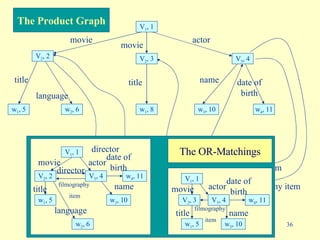
1 2 4 5 6 title language 7 3 year 8 director 9 name 10 movie date of birth 11 1983 movie actor Zelig Antz 1998 English 1/12/1935 Woody Allen title year filmography item filmography item v 1 v 2 w 1 v 3 title actor movie director filmography item w 2 w 3 w 4 date of birth name language The product of the query and the database is the next graph

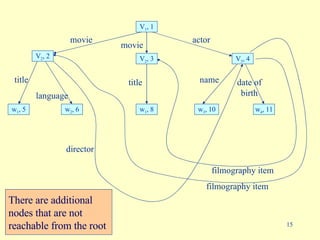
title language director name movie date of birth movie actor title filmography item filmography item V 1 , 1 V 2 , 2 V 2 , 3 V 3 , 4 w 1 , 5 w 2 , 6 w 1 , 8 w 3 , 10 w 4 , 11 There are additional nodes that are not reachable from the root

For a subgraph G of the product graph G has no repeated variables G contains the root Each node in G is reachable from the root G preserves the constraints (edges) of the query Conditions 1 – 3  OR-matching graph Conditions 1 – 4  weak-matching graph Matching as a Subgraph of the Product Graph

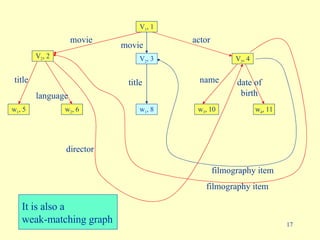
title language director name movie date of birth movie actor title filmography item filmography item V 1 , 1 V 2 , 2 V 2 , 3 V 3 , 4 w 1 , 5 w 2 , 6 w 1 , 8 w 3 , 10 w 4 , 11 An OR-matching graph It is also a weak-matching graph V 1 , 1 V 2 , 2 w 1 , 5 w 2 , 6 V 3 , 4 w 3 , 10 w 4 , 11

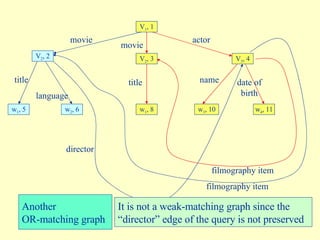
title language director name movie date of birth movie actor title filmography item filmography item V 1 , 1 V 2 , 2 V 2 , 3 V 3 , 4 w 1 , 5 w 2 , 6 w 1 , 8 w 3 , 10 w 4 , 11 V 1 , 1 V 3 , 4 w 3 , 10 w 4 , 11 Another OR-matching graph V 2 , 3 w 1 , 8 It is not a weak-matching graph since the “ director” edge of the query is not preserved

Matching Graphs Each OR-matching graph represents an OR-matching (and each weak-matching graph represent a weak matching) An OR-matching can be represented by many OR-matching graphs, but all these graphs have the same set of nodes and only differ by their edges (and the same it true for weak-matchings and weak-matching graphs) Matching

Intuition For DAG queries, matching graphs are constructed by adding edges according to the query constraints The order of the extensions is simply made by using a topological sort of the query nodes For cyclic queries, a simple traversal over the query nor a simple traversal over the database will work Instead, we use a stratum traversal over the matching graph

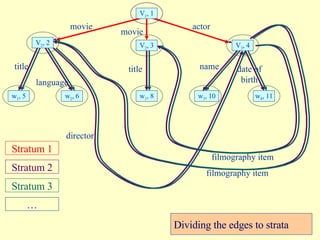
title language director name movie date of birth movie actor title filmography item filmography item V 1 , 1 V 2 , 2 V 2 , 3 V 3 , 4 w 1 , 5 w 2 , 6 w 1 , 8 w 3 , 10 w 4 , 11 Dividing the edges to strata … Stratum 1 Stratum 2 Stratum 3

Stratum Traversal A stratum traversal is an ordered list that Starts with the edges on stratum 1 Followed by the edges of stratum 2 … Followed by the edges of stratum n … The order of the edges in each stratum is unimportant There can be multiple occurrences of the same edge in different strata We only look at the first n strata, where n is the size of the query

Computing the OR-Matching Graphs A set of OR-matching graphs is created We extend each OR-matching graph in the set by adding edges according to the stratum traversal Initially, the set includes a single graph that consists only the root of the product graph In each extension step, we try to add the current edge to the graphs that were produced so far, and this may cause The creation of a new graph that replaces the extended graph The creation of a new graph that is added to the set of graphs in addition to the existing graphs No change to the set of graphs

Adding an Edge After each addition of an edge, subsumed matching-graphs are being removed, to avoid exponential blowup There are six cases that should be handled The cases of extending a graph by an edge will be described next

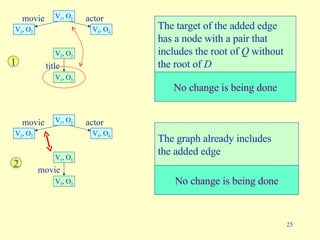
No change is being done movie V 1 , O 1 V 2 , O 2 actor V 3 , O 4 title V 2 , O 2 V 1 , O 3 The target of the added edge has a node with a pair that includes the root of Q without the root of D 1 No change is being done movie V 1 , O 1 V 2 , O 2 actor V 3 , O 4 movie V 1 , O 1 V 2 , O 2 The graph already includes the added edge 2

No change is being done movie V 1 , O 1 V 2 , O 2 actor V 3 , O 4 title V 2 , O 3 W 1 , O 8 The graph does not include the source of the added edge 3 movie V 1 , O 1 V 2 , O 2 actor V 3 , O 4 title V 2 , O 2 W 1 , O 5 The graph includes the source of the added edge and no node with the variable of the target 4 movie V 1 , O 1 V 2 , O 2 actor V 3 , O 4 title W 1 , O 5 The edge is added to the graph and the new graph replaces the existing graph

movie V 1 , O 1 V 2 , O 2 actor V 3 , O 4 The graph already includes the source and the target of the added edge but does not include the added edge itself 5 title W 1 , O 3 a.k.a V 2 , O 2 W 1 , O 3 The edge is added to the graph and the new graph replaces the existing graph a.k.a

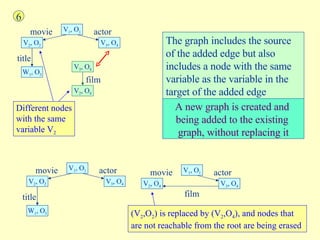
movie V 1 , O 1 V 2 , O 2 actor V 3 , O 4 film V 3 , O 4 V 2 , O 4 The graph includes the source of the added edge but also includes a node with the same variable as the variable in the target of the added edge 6 title W 1 , O 3 Different nodes with the same variable V 2 A new graph is created and being added to the existing graph, without replacing it movie V 1 , O 1 V 2 , O 2 actor V 3 , O 4 title W 1 , O 3 movie V 1 , O 1 V 2 , O 4 actor V 3 , O 4 film (V 2 ,O 2 ) is replaced by (V 2 ,O 4 ), and nodes that are not reachable from the root are being erased

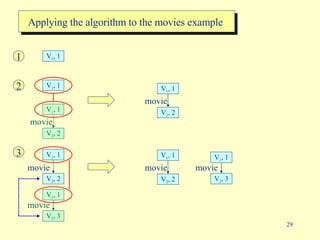
Applying the algorithm to the movies example V 1 , 1 1 V 1 , 1 2 movie V 2 , 2 V 1 , 1 movie V 2 , 2 V 1 , 1 3 movie V 2 , 2 V 1 , 1 V 1 , 1 V 2 , 3 movie movie V 2 , 2 V 1 , 1 V 1 , 1 V 2 , 3 movie

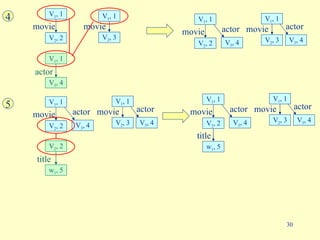
4 movie V 2 , 2 V 1 , 1 V 1 , 1 V 2 , 3 movie actor V 1 , 1 V 3 , 4 V 3 , 4 movie V 2 , 2 V 1 , 1 V 1 , 1 V 2 , 3 movie actor V 3 , 4 actor 5 title V 2 , 2 w 1 , 5 V 3 , 4 movie V 2 , 2 V 1 , 1 V 1 , 1 V 2 , 3 movie actor V 3 , 4 actor title w 1 , 5 V 3 , 4 movie V 2 , 2 V 1 , 1 V 1 , 1 V 2 , 3 movie actor V 3 , 4 actor

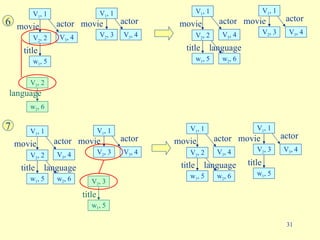
6 language V 2 , 2 w 2 , 6 title w 1 , 5 V 3 , 4 movie V 2 , 2 V 1 , 1 V 1 , 1 V 2 , 3 movie actor V 3 , 4 actor language w 2 , 6 title w 1 , 5 V 3 , 4 movie V 2 , 2 V 1 , 1 V 1 , 1 V 2 , 3 movie actor V 3 , 4 actor 7 language w 2 , 6 title w 1 , 5 V 3 , 4 movie V 2 , 2 V 1 , 1 V 1 , 1 V 2 , 3 movie actor V 3 , 4 actor title w 1 , 5 V 2 , 3 language w 2 , 6 title w 1 , 5 V 3 , 4 movie V 2 , 2 V 1 , 1 V 1 , 1 V 2 , 3 movie actor V 3 , 4 actor title w 1 , 5

language w 2 , 6 title w 1 , 5 V 3 , 4 movie V 1 , 1 V 2 , 3 movie actor V 3 , 4 actor title w 1 , 5 8 V 2 , 2 V 1 , 1 name V 3 , 4 w 3 , 10 name w 3 , 10 name w 3 , 10 V 3 , 4 w 4 , 11 date of birth 9 date of birth w 4 , 11 date of birth w 4 , 11

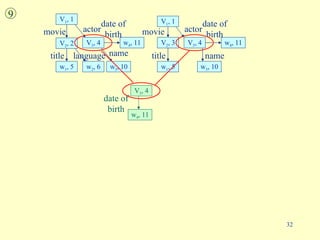
language w 2 , 6 title w 1 , 5 V 3 , 4 movie V 1 , 1 V 2 , 3 movie actor V 3 , 4 actor title w 1 , 5 10 director V 2 , 2 V 3 , 4 V 2 , 2 V 1 , 1 name w 3 , 10 name w 3 , 10 date of birth w 4 , 11 date of birth w 4 , 11 language w 2 , 6 title w 1 , 5 V 3 , 4 movie V 2 , 2 V 1 , 1 V 1 , 1 V 2 , 3 movie actor V 3 , 4 actor title w 1 , 5 name w 3 , 10 name w 3 , 10 date of birth w 4 , 11 date of birth w 4 , 11 director

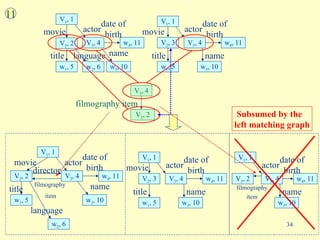
11 filmography item V 3 , 4 V 2 , 2 language w 2 , 6 title w 1 , 5 V 3 , 4 movie V 2 , 2 V 1 , 1 V 1 , 1 V 2 , 3 movie actor V 3 , 4 actor title w 1 , 5 name w 3 , 10 name w 3 , 10 date of birth w 4 , 11 date of birth w 4 , 11 title w 1 , 5 movie V 2 , 2 language w 2 , 6 V 3 , 4 V 1 , 1 V 1 , 1 V 2 , 3 movie actor V 3 , 4 actor title w 1 , 5 name w 3 , 10 name w 3 , 10 date of birth w 4 , 11 date of birth w 4 , 11 filmography item director V 1 , 1 V 2 , 2 V 3 , 4 actor name w 3 , 10 date of birth w 4 , 11 filmography item Subsumed by the left matching graph

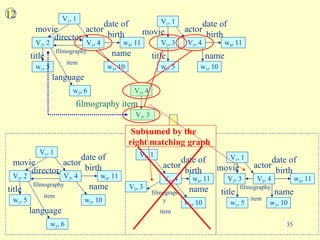
12 V 1 , 1 V 2 , 3 movie V 3 , 4 actor title w 1 , 5 name w 3 , 10 date of birth w 4 , 11 title w 1 , 5 movie V 2 , 2 language w 2 , 6 V 3 , 4 V 1 , 1 actor name w 3 , 10 date of birth w 4 , 11 filmography item director filmography item V 3 , 4 V 2 , 3 title w 1 , 5 movie V 2 , 2 language w 2 , 6 V 3 , 4 V 1 , 1 V 1 , 1 V 2 , 3 movie actor V 3 , 4 actor title w 1 , 5 name w 3 , 10 name w 3 , 10 date of birth w 4 , 11 date of birth w 4 , 11 filmography item director filmography item V 2 , 3 V 3 , 4 V 1 , 1 actor name w 3 , 10 date of birth w 4 , 11 filmography item Subsumed by the right matching graph

title language name movie date of birth movie actor title filmography item filmography item V 1 , 1 V 2 , 2 V 2 , 3 V 3 , 4 w 1 , 5 w 2 , 6 w 1 , 8 w 3 , 10 w 4 , 11 The Product Graph director title w 1 , 5 movie V 2 , 2 language w 2 , 6 V 3 , 4 V 1 , 1 actor name w 3 , 10 date of birth w 4 , 11 filmography item director V 1 , 1 V 2 , 3 movie V 3 , 4 actor title w 1 , 5 name w 3 , 10 date of birth w 4 , 11 filmography item The OR-Matchings

Computing Maximal Weak-Matching Graphs In order to compute maximal weak matching graphs, the same algorithm is being used with a slight change After each addition of an edge the nodes that cause a query constraint not to be preserved are removed (along with edges that contain these nodes) Also, are deleted nodes that the previous deletion causes them not to be reachable from the root

The Algorithm Computes Weak-Queries in Polynomial Time Theorem Given a query Q and a database D , the revised algorithm terminates with the set of maximal weak-matching graphs of Q w.r.t. D . The runtime of the algorithm is O ( q 3 dm 2 ), where q is the size of the query, d is the size of the database and m is the size of the result

�ݺ�ߣ

Computing FDs

Recommended

More Related Content

Similar to Computing FDs (20)

Recently uploaded (20)

Computing FDs