Comuter graphics bresenhams circle drawing algorithm
Download as pptx, pdf1 like524 views
Comuter graphics bresenhams circle drawing algorithm, extra solved examples on midpoint circle drawing algorithm,
1 of 5
Downloaded 12 times





Ad
Recommended
Comuter graphics ellipse drawing algorithm



Comuter graphics ellipse drawing algorithmRachana Marathe
?
Comuter graphics ellipse drawing algorithm, solved example for ellipse drawing algorithm, calculate pixel positions for ellipse, region1 , region 2, Lec05 circle ellipse



Lec05 circle ellipseMaaz Rizwan
?
This document discusses algorithms for drawing circles and ellipses in computer graphics. It covers:
1. Circle drawing algorithms including using Cartesian coordinates, polar coordinates, and the midpoint circle algorithm which iteratively calculates the midpoint between pixels to determine if they are inside, outside, or on the circle.
2. The midpoint ellipse algorithm which is similar but uses a modified decision parameter calculation that handles two regions for the first quadrant.
3. Key aspects of the algorithms include using octants and circle symmetry to reduce calculations, and translating the drawn shape to be centered at a given point.BressenhamˇŻs Midpoint Circle Drawing Algorithm



BressenhamˇŻs Midpoint Circle Drawing AlgorithmMrinmoy Dalal
?
This document explains Bresenham's midpoint circle drawing algorithm. It defines a circle as all points equidistant from a center point. The algorithm uses integer arithmetic to iteratively determine the next pixel on the circle circumference. It starts at an initial point and calculates a decision parameter P to determine if the next point is above or below along the y-axis. It tabulates an example of drawing a circle of radius 10 centered at the origin to demonstrate how P is used to progress around the circle octant by octant.Midpoint circle algo



Midpoint circle algoMohd Arif
?
The midpoint circle algorithm is similar to Bresenham's circle algorithm and uses the midpoint between pixels to determine whether the pixel is inside or outside a circle. It defines a decision parameter pi based on the midpoint and updates pi by integer amounts at each step to determine the next pixel along the circle. The initial value of pi is set to 5/4 - r when r is an integer to determine the first pixel.Bresenham circle



Bresenham circleTaher Barodawala
?
The document describes Bresenham's circle generation algorithm. It explains that circles have 8-point symmetry that can be exploited to only calculate a quarter circle. It derives the algorithm by interpolating discrete pixels along a small arc and choosing the pixel with minimum error. It determines the initial decision parameter and the recurrence relation to calculate the next decision parameter in the algorithm. The full pseudocode of the algorithm is also provided.Mid point circle algorithm



Mid point circle algorithmMani Kanth
?
This document describes the midpoint circle algorithm for drawing circles given a radius and center point. It works by starting at an initial point on the circumference, calculating a decision parameter, and then iteratively determining the next point by testing if the decision parameter is positive or negative and updating the parameter according to the point's coordinates. It also explains how to determine additional points in the other octants and shift the calculated pixel positions to be centered on the given center point.Computer Graphic - Lines, Circles and Ellipse



Computer Graphic - Lines, Circles and Ellipse2013901097
?
1. The document describes algorithms for drawing lines, circles, and ellipses using a midpoint technique. It provides examples showing the steps and calculations for applying each algorithm.
2. Key steps of the line drawing algorithm include calculating slope, change in x and y, and a decision parameter to determine the next point. Circles use a decision parameter comparing radius to x and y values. Ellipses use two regions and decision parameters involving radii and x/y values.
3. Examples are provided applying each algorithm to draw specific geometric shapes given endpoint or radius values. Tables show the calculations and plotted points at each iteration.Mid-Point Cirle Drawing Algorithm



Mid-Point Cirle Drawing AlgorithmNeha Kaurav
?
This document discusses algorithms for drawing circles using midpoint circle algorithm. It defines key circle concepts like radius, diameter and chord. It then explains the midpoint circle algorithm which uses 8-fold symmetry and computes pixel positions for only 45ˇă sector. The algorithm initializes the first point as (0, radius) and uses a decision parameter F to iteratively calculate the next pixel position as (x+1, y) if F < 0 or (x+1, y-1) if F >= 0 until x >= y. Pseudocode and a C program to implement the algorithm is also provided with an example.Circle drawing algo.



Circle drawing algo.Mohd Arif
?
This document describes Bresenham's circle algorithm for efficiently scan converting a circle. It begins by explaining the symmetry of a circle and prior inefficient polynomial and trigonometric methods. It then presents Bresenham's algorithm which takes advantage of the circle's symmetry and uses a decision variable to determine whether to move in the x or y direction to plot each pixel, ensuring points are always closest to the true circle. The algorithm is presented with variables initialized and steps to iterate through the first octant to plot all pixels.Bresenhamcircle derivation



Bresenhamcircle derivationMazharul Islam
?
The document describes Bresenham's circle generation algorithm. It utilizes the symmetry of circles to only calculate pixels in the first 45 degrees. It calculates the error between the actual circle curve and discrete pixels, choosing the pixel with lower error to trace the circle. It derives a decision parameter formula to iteratively calculate the next pixel, tracking whether to increase x or decrease y based on the sign of the decision parameter.Computer Graphics - Bresenham's line drawing algorithm & Mid Point Circle alg...



Computer Graphics - Bresenham's line drawing algorithm & Mid Point Circle alg...Saikrishna Tanguturu
?
The document discusses algorithms for drawing lines and circles on a digital display. It describes Bresenham's line drawing algorithm which plots discrete points along a line to approximate it on the pixel grid. It uses decision parameters to determine whether to increment the x or y coordinate to best fit the line. For circles, it explains using the midpoint circle algorithm which calculates decision parameters based on the distance of pixel midpoints to the circle boundary to iteratively plot points. The document provides pseudocode to implement Bresenham's circle algorithm. It also lists the initial values and decision parameter updates required.Ellipses drawing algo.



Ellipses drawing algo.Mohd Arif
?
(1) An ellipse is defined by the equation (x-h)2/a2 + (y-k)2/b2 = 1, where (h,k) is the center and a and b are the lengths of the major and minor axes.
(2) There are two methods to scan convert an ellipse - the polynomial method and trigonometric method.
(3) The midpoint ellipse algorithm uses a decision parameter p to recursively scan convert the ellipse pixel by pixel in a manner similar to the midpoint circle algorithm.Bresenhams



BresenhamsDharmendra Gupta
?
The document discusses algorithms for computer graphics including Bresenham's line drawing algorithm, circle drawing algorithms, and polygon filling algorithms. It introduces Bresenham's line drawing algorithm which uses integer calculations to incrementally determine which pixel is closer to the mathematical line. It then discusses a simple circle drawing algorithm and its limitations before introducing the more efficient mid-point circle drawing algorithm.Circle generation algorithm



Circle generation algorithmAnkit Garg
?
The document describes the Breshenham's circle generation algorithm. It explains that the algorithm uses a decision parameter to iteratively select pixels along the circumference of a circle. It provides pseudocode for the algorithm, which initializes x and y values, calculates a decision parameter, and increments x while decrementing y at each step, plotting points based on the decision parameter. An example of applying the algorithm to generate a circle with radius 5 is also provided.Finite elements : basis functions



Finite elements : basis functionsTarun Gehlot
?
1. The document discusses the basis functions used in 1D and 2D finite element analysis.
2. For 1D elements, it presents the linear, quadratic and cubic basis functions derived from imposing interpolation conditions on linear, quadratic and cubic shape functions respectively.
3. For 2D elements, it derives the linear and quadratic basis functions for triangular and rectangular elements by transforming the element coordinates and imposing interpolation conditions on linear and quadratic Ansatz shape functions.Bresenham circles and polygons derication



Bresenham circles and polygons dericationKumar
?
The document discusses algorithms for drawing lines and circles on a discrete pixel display. It begins by describing what characteristics an "ideal line" would have on such a display. It then introduces several algorithms for drawing lines, including the simple line algorithm, digital differential analyzer (DDA) algorithm, and Bresenham's line algorithm. The Bresenham algorithm is described in detail, as it uses only integer calculations. Next, a simple potential circle drawing algorithm is presented and its shortcomings discussed. Finally, the more accurate and efficient mid-point circle algorithm is described. This algorithm exploits the eight-way symmetry of circles and uses incremental calculations to determine the next pixel point.Bresenham's line algo.



Bresenham's line algo.Mohd Arif
?
Bresenham's line algorithm is an efficient method for drawing lines on a discrete grid such as a display. It works by calculating the next pixel to plot along the line based on the difference between the true and discrete slopes. It starts at the initial point and calculates a decision variable di to determine whether to plot the next point horizontally or diagonally. This variable is updated using the slope to continually track the closest path to the true line.Cs580



Cs580Chellamuthu K
?
The document discusses techniques for line drawing and generalization in computer graphics. It covers Bresenham's line drawing algorithm, which uses only integer arithmetic for efficiency. It also discusses circle drawing using the midpoint circle algorithm and extensions to draw ellipses. Anti-aliasing techniques like area sampling are introduced to reduce jagged edges when rasterizing lines.Bresenham's line drawing algorithm



Bresenham's line drawing algorithmMani Kanth
?
The Bresenham's line drawing algorithm is an incremental scan conversion algorithm that uses only integer calculations. It works by calculating the difference between the ideal y value and the actual plotted pixel y value at each x value, and determining whether to plot the pixel above or below the line based on whether this difference is positive or negative. The algorithm takes the line endpoints as input, calculates the change in x and y per step, sets an initial decision parameter, and then iteratively plots pixels, updating the decision parameter to determine whether to plot above or below the line at each step.Bresenham circlesandpolygons



Bresenham circlesandpolygonsaa11bb11
?
The document discusses algorithms for drawing lines and circles on a discrete pixel display. It begins by describing what characteristics an "ideal line" would have on such a display. It then introduces several algorithms for drawing lines, including the simple line algorithm, digital differential analyzer (DDA) algorithm, and Bresenham's line algorithm. The Bresenham algorithm is described in detail, as it uses only integer calculations. Next, a simple potential circle drawing algorithm is presented and its shortcomings discussed. Finally, the more accurate and efficient mid-point circle algorithm is introduced. This algorithm exploits the eight-way symmetry of circles and only calculates points in one octant.Graphics6 bresenham circlesandpolygons



Graphics6 bresenham circlesandpolygonsThirunavukarasu Mani
?
The document discusses several common algorithms for computer graphics rendering including Bresenham's line drawing algorithm, the midpoint circle algorithm, and scanline polygon filling. Bresenham's algorithm uses only integer calculations to efficiently draw lines. The midpoint circle algorithm incrementally chooses pixel coordinates to draw circles with eightfold symmetry and without floating point operations. Scanline polygon filling finds the edge intersections on each scanline and fills pixels between interior intersections.Mid point line Algorithm - Computer Graphics



Mid point line Algorithm - Computer GraphicsDrishti Bhalla
?
The document describes the midpoint line algorithm for plotting lines on a grid. It works by calculating the midpoint between each set of pixels and determining if it falls above or below the line to choose the next pixel. It only requires integer calculations, avoiding errors from division or multiplication. The algorithm is derived step-by-step and an example is provided to demonstrate how it is implemented to plot a line between two points.bresenham circles and polygons in computer graphics(Computer graphics tutorials)



bresenham circles and polygons in computer graphics(Computer graphics tutorials)Daroko blog(www.professionalbloggertricks.com)
?
Do Not just learn computer graphics an close your computer tab and go away..
APPLY them in real business,
Visit Daroko blog for real IT skills applications,androind, Computer graphics,Networking,Programming,IT jobs Types, IT news and applications,blogging,Builing a website, IT companies and how you can form yours, Technology news and very many More IT related subject.
-simply google:Daroko blog(professionalbloggertricks.com)
? Daroko blog (www.professionalbloggertricks.com)
? Presentation by Daroko blog, to see More tutorials more than this one here, Daroko blog has all tutorials related with IT course, simply visit the site by simply Entering the phrase Daroko blog (www.professionalbloggertricks.com) to search engines such as Google or yahoo!, learn some Blogging, affiliate marketing ,and ways of making Money with the computer graphic Applications(it is useless to learn all these tutorials when you can apply them as a student you know),also learn where you can apply all IT skills in a real Business Environment after learning Graphics another computer realate courses.ly
? Be practically real, not just academic reader
Parabola direction , vertex ,roots, minimum and maximum



Parabola direction , vertex ,roots, minimum and maximumNadeem Uddin
?
This document discusses quadratic functions of the form f(x) = ax^2 + bx + c. It provides details on:
1) The direction a parabola opens depending on whether a is positive or negative.
2) How to calculate the vertex (turning point) of a parabola using the formula (-b/2a, 4ac-b^2/4a).
3) How to calculate the roots (x-intercepts) of a quadratic function using the formula (-b ˇŔ ˇĚ(b^2 - 4ac))/2a.
Several examples are provided to demonstrate finding the direction, vertex, roots, minimum/maximum values of various quadratic functions.Local linear approximation



Local linear approximationTarun Gehlot
?
The document discusses local linear approximations, which provide a linear function that closely approximates a given non-linear function near a specific point. It defines the local linear approximation at a point x0 as f(x0) + f'(x0)(x - x0). Graphs and examples are provided to illustrate how the local linear approximation can be used to estimate function values close to x0. The concept of differentials is also introduced to estimate small changes in a function using its derivative. Examples demonstrate using differentials to approximate changes and estimate errors in computations involving measured values.Computer Graphic - Transformations in 3d



Computer Graphic - Transformations in 3d2013901097
?
1. The document describes the steps to perform a rotation of an object in 3D space about an arbitrary point or axis.
2. It provides an example of rotating a unit cube 90 degrees about an axis defined by two points and calculating the new coordinates.
3. It also gives an example of rotating the point (1,2,1) 90 degrees and showing the resulting point (1,2,3) transformed to (4,6,7).Bresenham derivation



Bresenham derivationKumar
?
The document derives Bresenham's line algorithm for drawing lines on a discrete grid. It starts with the line equation and defines variables for the slope and intercept. It then calculates the distance d1 and d2 from the line to two possible pixel locations and expresses their difference in terms of the slope and intercept. By multiplying this difference by the change in x, it removes the floating point slope value, resulting in an integer comparison expression. This is defined recursively to draw each subsequent pixel, using pre-computed constants. The initial p0 value is also derived from the line endpoint coordinates.Lab lecture 2 bresenham



Lab lecture 2 bresenhamsimpleok
?
Bresenham's line algorithm uses incremental integer calculations to determine which pixels to turn on when drawing a line on a pixel-based display. It works by calculating a decision parameter Pk at each step k to determine whether to plot the pixel at (Xk+1,Yk) or (Xk+1,Yk+1). For a given line from (30,20) to (40,28), the algorithm is applied by initializing P0=6 and then iteratively calculating Pk+1 at each step k by adding either 2dy or 2dy-2dx depending on whether Pk is positive or negative. This tracks the line from (30,20) to (40,28)Comuter graphics bresenhams line drawing algorithm



Comuter graphics bresenhams line drawing algorithmRachana Marathe
?
bresenhams line drawing algorithm examples, solved examples, computer graphics, pixel calculation, hearn and baker text book on computer graphics, extra solved examples on bresenhams line drawing algorithm,
Ad
More Related Content
What's hot (20)
Circle drawing algo.



Circle drawing algo.Mohd Arif
?
This document describes Bresenham's circle algorithm for efficiently scan converting a circle. It begins by explaining the symmetry of a circle and prior inefficient polynomial and trigonometric methods. It then presents Bresenham's algorithm which takes advantage of the circle's symmetry and uses a decision variable to determine whether to move in the x or y direction to plot each pixel, ensuring points are always closest to the true circle. The algorithm is presented with variables initialized and steps to iterate through the first octant to plot all pixels.Bresenhamcircle derivation



Bresenhamcircle derivationMazharul Islam
?
The document describes Bresenham's circle generation algorithm. It utilizes the symmetry of circles to only calculate pixels in the first 45 degrees. It calculates the error between the actual circle curve and discrete pixels, choosing the pixel with lower error to trace the circle. It derives a decision parameter formula to iteratively calculate the next pixel, tracking whether to increase x or decrease y based on the sign of the decision parameter.Computer Graphics - Bresenham's line drawing algorithm & Mid Point Circle alg...



Computer Graphics - Bresenham's line drawing algorithm & Mid Point Circle alg...Saikrishna Tanguturu
?
The document discusses algorithms for drawing lines and circles on a digital display. It describes Bresenham's line drawing algorithm which plots discrete points along a line to approximate it on the pixel grid. It uses decision parameters to determine whether to increment the x or y coordinate to best fit the line. For circles, it explains using the midpoint circle algorithm which calculates decision parameters based on the distance of pixel midpoints to the circle boundary to iteratively plot points. The document provides pseudocode to implement Bresenham's circle algorithm. It also lists the initial values and decision parameter updates required.Ellipses drawing algo.



Ellipses drawing algo.Mohd Arif
?
(1) An ellipse is defined by the equation (x-h)2/a2 + (y-k)2/b2 = 1, where (h,k) is the center and a and b are the lengths of the major and minor axes.
(2) There are two methods to scan convert an ellipse - the polynomial method and trigonometric method.
(3) The midpoint ellipse algorithm uses a decision parameter p to recursively scan convert the ellipse pixel by pixel in a manner similar to the midpoint circle algorithm.Bresenhams



BresenhamsDharmendra Gupta
?
The document discusses algorithms for computer graphics including Bresenham's line drawing algorithm, circle drawing algorithms, and polygon filling algorithms. It introduces Bresenham's line drawing algorithm which uses integer calculations to incrementally determine which pixel is closer to the mathematical line. It then discusses a simple circle drawing algorithm and its limitations before introducing the more efficient mid-point circle drawing algorithm.Circle generation algorithm



Circle generation algorithmAnkit Garg
?
The document describes the Breshenham's circle generation algorithm. It explains that the algorithm uses a decision parameter to iteratively select pixels along the circumference of a circle. It provides pseudocode for the algorithm, which initializes x and y values, calculates a decision parameter, and increments x while decrementing y at each step, plotting points based on the decision parameter. An example of applying the algorithm to generate a circle with radius 5 is also provided.Finite elements : basis functions



Finite elements : basis functionsTarun Gehlot
?
1. The document discusses the basis functions used in 1D and 2D finite element analysis.
2. For 1D elements, it presents the linear, quadratic and cubic basis functions derived from imposing interpolation conditions on linear, quadratic and cubic shape functions respectively.
3. For 2D elements, it derives the linear and quadratic basis functions for triangular and rectangular elements by transforming the element coordinates and imposing interpolation conditions on linear and quadratic Ansatz shape functions.Bresenham circles and polygons derication



Bresenham circles and polygons dericationKumar
?
The document discusses algorithms for drawing lines and circles on a discrete pixel display. It begins by describing what characteristics an "ideal line" would have on such a display. It then introduces several algorithms for drawing lines, including the simple line algorithm, digital differential analyzer (DDA) algorithm, and Bresenham's line algorithm. The Bresenham algorithm is described in detail, as it uses only integer calculations. Next, a simple potential circle drawing algorithm is presented and its shortcomings discussed. Finally, the more accurate and efficient mid-point circle algorithm is described. This algorithm exploits the eight-way symmetry of circles and uses incremental calculations to determine the next pixel point.Bresenham's line algo.



Bresenham's line algo.Mohd Arif
?
Bresenham's line algorithm is an efficient method for drawing lines on a discrete grid such as a display. It works by calculating the next pixel to plot along the line based on the difference between the true and discrete slopes. It starts at the initial point and calculates a decision variable di to determine whether to plot the next point horizontally or diagonally. This variable is updated using the slope to continually track the closest path to the true line.Cs580



Cs580Chellamuthu K
?
The document discusses techniques for line drawing and generalization in computer graphics. It covers Bresenham's line drawing algorithm, which uses only integer arithmetic for efficiency. It also discusses circle drawing using the midpoint circle algorithm and extensions to draw ellipses. Anti-aliasing techniques like area sampling are introduced to reduce jagged edges when rasterizing lines.Bresenham's line drawing algorithm



Bresenham's line drawing algorithmMani Kanth
?
The Bresenham's line drawing algorithm is an incremental scan conversion algorithm that uses only integer calculations. It works by calculating the difference between the ideal y value and the actual plotted pixel y value at each x value, and determining whether to plot the pixel above or below the line based on whether this difference is positive or negative. The algorithm takes the line endpoints as input, calculates the change in x and y per step, sets an initial decision parameter, and then iteratively plots pixels, updating the decision parameter to determine whether to plot above or below the line at each step.Bresenham circlesandpolygons



Bresenham circlesandpolygonsaa11bb11
?
The document discusses algorithms for drawing lines and circles on a discrete pixel display. It begins by describing what characteristics an "ideal line" would have on such a display. It then introduces several algorithms for drawing lines, including the simple line algorithm, digital differential analyzer (DDA) algorithm, and Bresenham's line algorithm. The Bresenham algorithm is described in detail, as it uses only integer calculations. Next, a simple potential circle drawing algorithm is presented and its shortcomings discussed. Finally, the more accurate and efficient mid-point circle algorithm is introduced. This algorithm exploits the eight-way symmetry of circles and only calculates points in one octant.Graphics6 bresenham circlesandpolygons



Graphics6 bresenham circlesandpolygonsThirunavukarasu Mani
?
The document discusses several common algorithms for computer graphics rendering including Bresenham's line drawing algorithm, the midpoint circle algorithm, and scanline polygon filling. Bresenham's algorithm uses only integer calculations to efficiently draw lines. The midpoint circle algorithm incrementally chooses pixel coordinates to draw circles with eightfold symmetry and without floating point operations. Scanline polygon filling finds the edge intersections on each scanline and fills pixels between interior intersections.Mid point line Algorithm - Computer Graphics



Mid point line Algorithm - Computer GraphicsDrishti Bhalla
?
The document describes the midpoint line algorithm for plotting lines on a grid. It works by calculating the midpoint between each set of pixels and determining if it falls above or below the line to choose the next pixel. It only requires integer calculations, avoiding errors from division or multiplication. The algorithm is derived step-by-step and an example is provided to demonstrate how it is implemented to plot a line between two points.bresenham circles and polygons in computer graphics(Computer graphics tutorials)



bresenham circles and polygons in computer graphics(Computer graphics tutorials)Daroko blog(www.professionalbloggertricks.com)
?
Do Not just learn computer graphics an close your computer tab and go away..
APPLY them in real business,
Visit Daroko blog for real IT skills applications,androind, Computer graphics,Networking,Programming,IT jobs Types, IT news and applications,blogging,Builing a website, IT companies and how you can form yours, Technology news and very many More IT related subject.
-simply google:Daroko blog(professionalbloggertricks.com)
? Daroko blog (www.professionalbloggertricks.com)
? Presentation by Daroko blog, to see More tutorials more than this one here, Daroko blog has all tutorials related with IT course, simply visit the site by simply Entering the phrase Daroko blog (www.professionalbloggertricks.com) to search engines such as Google or yahoo!, learn some Blogging, affiliate marketing ,and ways of making Money with the computer graphic Applications(it is useless to learn all these tutorials when you can apply them as a student you know),also learn where you can apply all IT skills in a real Business Environment after learning Graphics another computer realate courses.ly
? Be practically real, not just academic reader
Parabola direction , vertex ,roots, minimum and maximum



Parabola direction , vertex ,roots, minimum and maximumNadeem Uddin
?
This document discusses quadratic functions of the form f(x) = ax^2 + bx + c. It provides details on:
1) The direction a parabola opens depending on whether a is positive or negative.
2) How to calculate the vertex (turning point) of a parabola using the formula (-b/2a, 4ac-b^2/4a).
3) How to calculate the roots (x-intercepts) of a quadratic function using the formula (-b ˇŔ ˇĚ(b^2 - 4ac))/2a.
Several examples are provided to demonstrate finding the direction, vertex, roots, minimum/maximum values of various quadratic functions.Local linear approximation



Local linear approximationTarun Gehlot
?
The document discusses local linear approximations, which provide a linear function that closely approximates a given non-linear function near a specific point. It defines the local linear approximation at a point x0 as f(x0) + f'(x0)(x - x0). Graphs and examples are provided to illustrate how the local linear approximation can be used to estimate function values close to x0. The concept of differentials is also introduced to estimate small changes in a function using its derivative. Examples demonstrate using differentials to approximate changes and estimate errors in computations involving measured values.Computer Graphic - Transformations in 3d



Computer Graphic - Transformations in 3d2013901097
?
1. The document describes the steps to perform a rotation of an object in 3D space about an arbitrary point or axis.
2. It provides an example of rotating a unit cube 90 degrees about an axis defined by two points and calculating the new coordinates.
3. It also gives an example of rotating the point (1,2,1) 90 degrees and showing the resulting point (1,2,3) transformed to (4,6,7).Bresenham derivation



Bresenham derivationKumar
?
The document derives Bresenham's line algorithm for drawing lines on a discrete grid. It starts with the line equation and defines variables for the slope and intercept. It then calculates the distance d1 and d2 from the line to two possible pixel locations and expresses their difference in terms of the slope and intercept. By multiplying this difference by the change in x, it removes the floating point slope value, resulting in an integer comparison expression. This is defined recursively to draw each subsequent pixel, using pre-computed constants. The initial p0 value is also derived from the line endpoint coordinates.Lab lecture 2 bresenham



Lab lecture 2 bresenhamsimpleok
?
Bresenham's line algorithm uses incremental integer calculations to determine which pixels to turn on when drawing a line on a pixel-based display. It works by calculating a decision parameter Pk at each step k to determine whether to plot the pixel at (Xk+1,Yk) or (Xk+1,Yk+1). For a given line from (30,20) to (40,28), the algorithm is applied by initializing P0=6 and then iteratively calculating Pk+1 at each step k by adding either 2dy or 2dy-2dx depending on whether Pk is positive or negative. This tracks the line from (30,20) to (40,28)Computer Graphics - Bresenham's line drawing algorithm & Mid Point Circle alg...



Computer Graphics - Bresenham's line drawing algorithm & Mid Point Circle alg...Saikrishna Tanguturu
?
bresenham circles and polygons in computer graphics(Computer graphics tutorials)



bresenham circles and polygons in computer graphics(Computer graphics tutorials)Daroko blog(www.professionalbloggertricks.com)
?
Similar to Comuter graphics bresenhams circle drawing algorithm (20)
Comuter graphics bresenhams line drawing algorithm



Comuter graphics bresenhams line drawing algorithmRachana Marathe
?
bresenhams line drawing algorithm examples, solved examples, computer graphics, pixel calculation, hearn and baker text book on computer graphics, extra solved examples on bresenhams line drawing algorithm,
7. Bresenharms Circle Generation Algo_c8503330f911dd9ec76af8508bc0728d.pptx



7. Bresenharms Circle Generation Algo_c8503330f911dd9ec76af8508bc0728d.pptxghosharkoprabho
?
Iot thingsCircle algorithm



Circle algorithmPooja Dixit
?
The document describes the midpoint circle algorithm for drawing circles on a pixel screen. It explains how the algorithm determines the midpoint between the next two possible consecutive pixels and checks if the midpoint is inside or outside the circle to determine which pixel to illuminate. It provides the mathematical equations and steps used to iteratively calculate the x and y coordinates of each pixel on the circle. The algorithm is implemented in a C++ program to draw a circle on a graphics screen.Computer Graphics - lines, Circles and ellipse



Computer Graphics - lines, Circles and ellipseHisham Al Kurdi, EAVA, DMC-D-4K, HCCA-P, HCAA-D
?
1. The document describes algorithms for drawing lines, circles, and ellipses using a midpoint technique. It provides examples showing the steps and calculations to draw various shapes.
2. Key steps in the line algorithm include calculating slope, increment values, and a decision parameter to determine the next point. Circle and ellipse algorithms similarly use initial points, decision parameters, and region-based steps to iteratively plot points.
3. Examples show the incremental calculations and points plotted to draw lines between points, circles with given radii, and ellipses with specified rx and ry values.17 integrals of rational functions x



17 integrals of rational functions xmath266
?
This document discusses integrating rational functions. It begins by defining rational functions as functions of the form P(x)/Q(x) where P and Q are polynomials. It states that integrating rational functions involves decomposing them into simpler fractions using the Rational Decomposition Theorem. Examples are then provided to demonstrate how to decompose rational functions and integrate each term using substitution.Computer_Graphics_circle_drawing_techniq.ppt



Computer_Graphics_circle_drawing_techniq.pptAliZaib71
?
This document discusses different techniques for drawing circles in computer graphics. It begins by defining what a circle is mathematically. It then describes three main techniques: using Cartesian coordinates, polar coordinates, and the midpoint circle algorithm. The midpoint circle algorithm is described in detail as being the most efficient technique. It works by incrementally calculating decision parameters to determine the next pixel on the circle boundary using integer arithmetic rather than floating point calculations.10994479.ppt



10994479.pptALIZAIB KHAN
?
This document discusses different techniques for drawing circles in computer graphics, including Cartesian coordinates, polar coordinates, and the midpoint circle algorithm. Cartesian coordinates directly use the circle equation to plot points, but is inefficient due to calculations and gaps. Polar coordinates express the circle in parametric form using angle and radius, which solves the gap issue but still requires floating-point calculations. The midpoint circle algorithm derives a decision parameter to iteratively select the next point using integer increments, making it the most efficient method.Lines and curves algorithms



Lines and curves algorithmsMohammad Sadiq
?
The document discusses algorithms for drawing lines and circles on raster displays. It describes Bresenham's line algorithm which uses only integer calculations to determine which pixels to turn on along a line. For circles, it presents the midpoint circle algorithm which uses incremental integer calculations and the implicit equation of a circle to determine the pixel positions along the circle boundary.Bresenham's line algorithm



Bresenham's line algorithmPooja Dixit
?
The document summarizes Bresenham's line drawing algorithm. It derives the equations for calculating the next pixel position when drawing a line on a digital display. It considers cases where the slope is less than or equal to 1 and greater than 1. For each case, it calculates the distance from intersection points to pixel positions and derives the decision parameter equation to determine the next pixel.mid point algorithm.pdf



mid point algorithm.pdfMehulMunshi3
?
The document describes the mid-point circle algorithm for drawing circles. It uses eight-way symmetry to only calculate points for one octant of the circle, then uses symmetry to get the remaining points. At each x-coordinate, it must choose between two possible y-coordinates by calculating the mid-point between them and determining which side of the circle it falls on based on comparing the mid-point to the circle equation. It iterates this process, incrementally updating values for efficiency, until all points along the top-right octant are drawn, then uses symmetry to plot the full circle.CG08 - BresenhamˇŻs Line Algorithm Data structure.pdf



CG08 - BresenhamˇŻs Line Algorithm Data structure.pdfshehzadshafique51
?
BresenhamˇŻs Line Algorithm Data structuregroup3ppt-240508074515-Engineering Mathematics II Presentation.pptx



group3ppt-240508074515-Engineering Mathematics II Presentation.pptxAmolAher20
?
Engineering Mathematics II Presentation
Kelompok 1



Kelompok 1teddy
?
The document discusses circle equations with a given center point and radius. It provides the general equation for finding the distance between two points and uses this to derive the equation of a circle given its center P(-2,3) and passing through point Q(4,-1). It then shows the equations for circles with this center that meet exactly one point X and one point Y.Unit-2 raster scan graphics,line,circle and polygon algorithms



Unit-2 raster scan graphics,line,circle and polygon algorithmsAmol Gaikwad
?
This document provides information about raster scan graphics and algorithms for drawing lines, circles, and polygons in raster graphics. It begins with an introduction to raster scan graphics and line drawing concepts. It then describes the Digital Differential Analyzer (DDA) line drawing algorithm and provides an example of how to use it to rasterize a line. Next, it explains Bresenham's line drawing algorithm and provides another example of using it to rasterize a line. Finally, it includes C program code implementations of the DDA and Bresenham's algorithms.Sbma 4603 numerical methods Assignment



Sbma 4603 numerical methods AssignmentSaidatina Khadijah
?
1. The document contains solutions to numerical methods problems involving roots, derivatives, approximations of fractions in binary, and matrix factorization.
2. For problem 1, the student computes derivatives of a function f(x) up to the 9th derivative to solve for roots of a polynomial.
3. For problem 2, the student uses binary approximations to find fractional representations of 1/3, 8/15, and 1/10 + 1/5 - 1/6.
4. For problem 3, the student proves a property of infinite geometric series and converts the decimal 8/7 to binary.
5. For problem 4, the student factors a coefficient matrix into upper and lower triangular matrices.Geometry Transformation



Geometry TransformationRose Mary Tania Arini
?
The document summarizes different types of geometry transformations:
1. Translations move every point on a shape by a distance and direction without changing the shape.
2. Reflections produce mirror images of shapes across lines or axes.
3. Rotations turn shapes around a fixed point by a certain angle.
4. Dilations enlarge or reduce the size of shapes around a fixed point but do not alter their form.
Composing multiple transformations means applying one transformation to the output of another. Matrix representations can describe the combined effect of transformations.NCERT Class 9 Maths Polynomials



NCERT Class 9 Maths PolynomialsPankajGahlot2
?
The document discusses polynomials and their properties. It defines zeros of a polynomial as numbers that make the polynomial equal to 0 when substituted in. It provides examples of finding zeros and using the remainder and factor theorems. It also covers factorizing polynomials using identities and splitting the middle term. Key polynomial identities are presented along with examples of expanding and factorizing polynomial expressions.Working principle of dda and bresenham line drawing explaination with example



Working principle of dda and bresenham line drawing explaination with exampleAashish Adhikari
?
Bresenham's Line Algorithm
This algorithm is used for scan converting a line. It was developed by Bresenham. It is an efficient method because it involves only integer addition, subtractions, and multiplication operations. These operations can be performed very rapidly so lines can be generated quickly.
In this method, next pixel selected is that one who has the least distance from true line.Tugas matematika menemukan konsep persamaan kuadrat



Tugas matematika menemukan konsep persamaan kuadrattrisnasariasih
?
1. The document describes solving several quadratic equations by factoring, completing the square, and using the quadratic formula. It provides examples of finding the roots of quadratic equations in various forms.
2. Methods for solving quadratic equations discussed include factoring, completing the square to convert it into the standard form of a quadratic equation, and using the quadratic formula.
3. Several examples are worked through step-by-step to demonstrate these different methods of solving quadratic equations algebraically.Ad
Recently uploaded (20)
Artificial intelligence and machine learning.pptx



Artificial intelligence and machine learning.pptxrakshanatarajan005
?
Artificial Intelligence full dataMode-Wise Corridor Level Travel-Time Estimation Using Machine Learning Models



Mode-Wise Corridor Level Travel-Time Estimation Using Machine Learning ModelsJournal of Soft Computing in Civil Engineering
?
This research is oriented towards exploring mode-wise corridor level travel-time estimation using Machine learning techniques such as Artificial Neural Network (ANN) and Support Vector Machine (SVM). Authors have considered buses (equipped with in-vehicle GPS) as the probe vehicles and attempted to calculate the travel-time of other modes such as cars along a stretch of arterial roads. The proposed study considers various influential factors that affect travel time such as road geometry, traffic parameters, location information from the GPS receiver and other spatiotemporal parameters that affect the travel-time. The study used a segment modeling method for segregating the data based on identified bus stop locations. A k-fold cross-validation technique was used for determining the optimum model parameters to be used in the ANN and SVM models. The developed models were tested on a study corridor of 59.48 km stretch in Mumbai, India. The data for this study were collected for a period of five days (Monday-Friday) during the morning peak period (from 8.00 am to 11.00 am). Evaluation scores such as MAPE (mean absolute percentage error), MAD (mean absolute deviation) and RMSE (root mean square error) were used for testing the performance of the models. The MAPE values for ANN and SVM models are 11.65 and 10.78 respectively. The developed model is further statistically validated using the Kolmogorov-Smirnov test. The results obtained from these tests proved that the proposed model is statistically valid.Empowering Electric Vehicle Charging Infrastructure with Renewable Energy Int...



Empowering Electric Vehicle Charging Infrastructure with Renewable Energy Int...AI Publications
?
The escalating energy crisis, heightened environmental awareness and the impacts of climate change have driven global efforts to reduce carbon emissions. A key strategy in this transition is the adoption of green energy technologies particularly for charging electric vehicles (EVs). According to the U.S. Department of Energy, EVs utilize approximately 60% of their input energy during operation, twice the efficiency of conventional fossil fuel vehicles. However, the environmental benefits of EVs are heavily dependent on the source of electricity used for charging. This study examines the potential of renewable energy (RE) as a sustainable alternative for electric vehicle (EV) charging by analyzing several critical dimensions. It explores the current RE sources used in EV infrastructure, highlighting global adoption trends, their advantages, limitations, and the leading nations in this transition. It also evaluates supporting technologies such as energy storage systems, charging technologies, power electronics, and smart grid integration that facilitate RE adoption. The study reviews RE-enabled smart charging strategies implemented across the industry to meet growing global EV energy demands. Finally, it discusses key challenges and prospects associated with grid integration, infrastructure upgrades, standardization, maintenance, cybersecurity, and the optimization of energy resources. This review aims to serve as a foundational reference for stakeholders and researchers seeking to advance the sustainable development of RE based EV charging systems.Generative AI & Large Language Models Agents



Generative AI & Large Language Models Agentsaasgharbee22seecs
?
Generative AI & Large Language Models Agents SICPA: Fabien Keller - background introduction



SICPA: Fabien Keller - background introductionfabienklr
?
Dear SICPA Team,
Please find attached a document outlining my professional background and experience.
I remain at your disposal should you have any questions or require further information.
Best regards,
Fabien KellerApplications of Centroid in Structural Engineering



Applications of Centroid in Structural Engineeringsuvrojyotihalder2006
?
Applications of Centroid in Structural EngineeringMachine foundation notes for civil engineering students



Machine foundation notes for civil engineering studentsDYPCET
?
Machine foundation short notes for engineering students22PCOAM16 ML Unit 3 Full notes PDF & QB.pdf



22PCOAM16 ML Unit 3 Full notes PDF & QB.pdfGuru Nanak Technical Institutions
?
22PCOAM16 ML Unit 3 notes PDF & QB. pdfFrontend Architecture Diagram/Guide For Frontend Engineers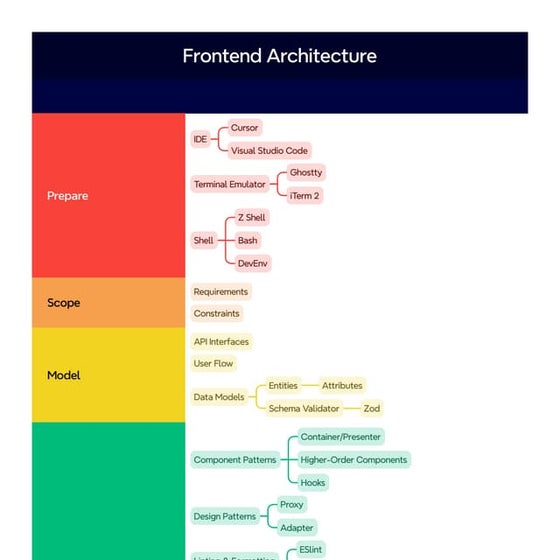



Frontend Architecture Diagram/Guide For Frontend EngineersMichael Hertzberg
?
Frontend Architecture chart I made using XMind. No AI help here <3.hypermedia_system_revisit_roy_fielding .



hypermedia_system_revisit_roy_fielding .±·´ˇµţł˘´ˇł§ÖęĘ˝»áÉç
?
¤ł¤ÎŮYÁϤϡ˘Roy Fielding¤ÎRESTŐ“ÎÄŁ¨µÚ5ŐÂŁ©¤ňŐń¤ę·µ¤ęˇ˘¬F´úWeb¤ÇŐ`˝â¤µ¤ě¤¬¤Á¤ĘREST¤Î±ľŮ|¤ň˝âŐh¤·¤Ć¤¤¤Ţ¤ąˇŁĚؤˡ˘ĄĎĄ¤ĄŃ©`ĄáĄÇĄŁĄ˘ÖĆÓů¤äĄ˘Ą×ĄęĄ±©`Ą·ĄçĄó×´‘B¤ÎąÜŔí¤Ëév¤ą¤ëÖŘŇŞ¤ĘĄÝĄ¤ĄóĄČ¤ň¤ď¤«¤ę¤ä¤ą¤Ż˝B˝é¤·¤Ć¤¤¤Ţ¤ąˇŁ
This presentation revisits Chapter 5 of Roy Fielding's PhD dissertation on REST, clarifying concepts that are often misunderstood in modern web designˇŞsuch as hypermedia controls within representations and the role of hypermedia in managing application state.ML_Unit_V_RDC_ASSOCIATION AND DIMENSIONALITY REDUCTION.pdf



ML_Unit_V_RDC_ASSOCIATION AND DIMENSIONALITY REDUCTION.pdframeshwarchintamani
?
Association Rules-Market Basket Analysis, The Apriori Algorithm, Performance
Measures ¨C Support, Confidence, Lift. Dimensionality Reduction: Principal Component
Analysis, Partial Least Squares Subset Selection, Feature Reduction/Dimensionality
reduction, Principal components analysis (Eigen values, Eigen vectors, Orthogonality)Mode-Wise Corridor Level Travel-Time Estimation Using Machine Learning Models



Mode-Wise Corridor Level Travel-Time Estimation Using Machine Learning ModelsJournal of Soft Computing in Civil Engineering
?
Ad
Comuter graphics bresenhams circle drawing algorithm
- 1. COMPUTER GRAPHICS Bressenham's Circle Drawing Algorithm By: Ms. Rachana Marathe
- 2. Bressenham's algorithm: Circle drawing from x=0 and x=y ex: if r=10, (x0,y0)= (0,10) p0 =1-r if Pk<0 then (xk+1,yk) and pk+1= pk+2xk+1+1 else (pk>0) then (xk+1,yk-1) and pk+1= pk+2xk+1+1-2yk+1
- 3. Example 1: radius = 5 Algorithm: ex: if r=radius, (x0,y0)= (0,r) p0 =1-r if Pk<0 then (xk+1,yk) and pk+1= pk+2xk+1+1 else (pk>0) then (xk+1,yk-1) and pk+1= pk+2xk+1+1-2yk+1 Solution: X=0, r=5 , so plot first point at ( 0,5) p0 =1-r = 1-5 = -4 X=1 , y=5 (if case) pk+1= pk+2xk+1+1 = -4+2+1 = -1 X=2, y=5 (if case) pk+1= pk+2xk+1+1 = -1 + 4+1 = 4 X= 3 y = 4 (else case) pk+1= pk+2xk+1+1-2yk+1 = 4+6+1 ¨C 8=3 X=4, y = 3 (else case) X>y hence STOP
- 4. Therefore the pixels are (0,5) (1,5) (2,5) (3,4) (4,3)
- 5. Reference Hearn,Baker - Computer Graphics - C Version 2nd Ed http://edu.uokufa.edu.iq/staff/dr.nidhal/compressed%20comp.book/H earn,Baker%20-%20Computer%20Graphics%20- %20C%20Version%202nd%20Ed.pdf










