Conic section
Download as PPTX, PDF1 like311 views
This document discusses conic sections, which are curves formed by the intersection of a cone with a plane. The three types of conic sections are circles, ellipses, and hyperbolas. Parabolas are also conic sections. Circles are defined as all points equidistant from a center point. Ellipses are defined as all points whose sum of distances to two focal points is a constant. Hyperbolas are defined as two branches where the difference between the distances to two focal points is a constant. The eccentricity parameter relates the conic section's shape to the distance between its foci and directrix.
1 of 30
Downloaded 72 times



















Recommended
Conic sections



Conic sectionsdarencervantes
Ėý
This document discusses the four types of conic sections: circles, ellipses, parabolas, and hyperbolas. It provides the geometric definitions of each conic section. Circles are formed from a plane cutting a cone perpendicular to the axis. Parabolas are the locus of all points equidistant from a focus and directrix. Ellipses are defined as having the sum of the distances to two foci being constant. Hyperbolas have the difference between the distances to two foci as the constant value.32 conic sections, circles and completing the square



32 conic sections, circles and completing the squaremath126
Ėý
Conic sections are curves formed by the intersection of a plane and a right circular cone. The document discusses four types of conic sections: circles, ellipses, parabolas, and hyperbolas. Circles are defined as points equidistant from a fixed center point, while ellipses are defined as points whose sum of distances to two fixed foci is constant.Conic section ppt



Conic section pptFarhana Shaheen
Ėý
This document provides information about different conic sections including circles, parabolas, ellipses, and hyperbolas. It defines each conic section, gives their key properties and equations, and provides examples of how they appear in nature. The three conic sections that are created when a double cone is intersected with a plane are parabolas, circles and ellipses, and hyperbolas. Each type of conic section is defined by its focal properties and relationships.Pre-Calculus 11 - Lesson no. 1: Conic Sections



Pre-Calculus 11 - Lesson no. 1: Conic SectionsJuan Miguel Palero
Ėý
This is a powerpoint presentation that discusses about the topic or lesson: Conic Sections. It also includes the definition, types and some terminologies involved in the topic: Conic Sections.CONIC SECTIONS AND ITS APPLICATIONS



CONIC SECTIONS AND ITS APPLICATIONSJaffer Sheriff
Ėý
This document defines and provides examples of different types of conic sections - parabolas, ellipses, and hyperbolas. It explains that conic sections are curves formed by the intersection of a plane with a cone, and that points on a conic section have a fixed ratio between their distance to a focus point and its directrix line, known as eccentricity. Eccentricity values distinguish the different conic section types. Examples of each in diagrams and applications like planetary orbits, bicycle gears, and network synchronization are also provided.Conic Sections (Class 11 Project)



Conic Sections (Class 11 Project)KushagraAgrawal46
Ėý
This document is a mathematics project submitted by Kushagra Agrawal to Kamal Soni Sir. It includes an acknowledgement thanking Kamal Soni Sir for providing guidance. The project contains information on different types of conic sections (parabolas, ellipses, hyperbolas, and circles) including their definitions, common features, examples, and applications. It also discusses the latus rectum and eccentricity of conic sections. The project was created using PowerPoint and includes references.Conic sections and introduction to circles



Conic sections and introduction to circlesArric Tan
Ėý
Conic sections are shapes that result from slicing a cone with a plane. There are four types of conic sections: circles, ellipses, parabolas, and hyperbolas. Circles can be defined by the general formula x^2 + y^2 = r^2, where all points are a distance r from the center. The center and radius of a circle can be determined by shifting the circle and setting the x and y components to 0.Applications of conic and vectors



Applications of conic and vectorsNauman Shafqat
Ėý
This document discusses applications of vectors and conics in multivariable calculus. It provides definitions of conic sections including parabolas, circles, ellipses, and hyperbolas. Applications of conics discussed include using the elliptical path of reflection in lithotripsy to break up kidney stones, the design of whispering galleries, and elliptical billiard tables. Additional applications mentioned are the elliptical orbit of planets and the use of parabolic mirrors. Examples of vector applications given are determining landing points while crossing a river, accounting for wind in airplane flight, and the orbital radius vector of planets around the sun.Applications of conic sections3



Applications of conic sections3Iram Khan
Ėý
This document discusses applications of various conic sections in real life. It begins by defining conic sections as curves derived from slicing a double-napped cone and lists the main types - parabolas, ellipses, circles, and hyperbolas. It then provides examples of applications for each type of conic section, such as parabolas in football trajectories, ellipses in eye shapes and planet orbits, circles in wheels and records, and hyperbolas in sonic booms and lighthouse beams. The document aims to illustrate how conic sections appear frequently in architecture, engineering, and natural phenomena.Conic section



Conic sectionAaryanMaheshwari
Ėý
This document discusses the four types of conic sections: circles, parabolas, ellipses, and hyperbolas. Each conic section is defined by its geometric properties and standard equation. Examples are given of real-life applications of each conic section, such as circles used in giant wheels and parabolas used in bridges and satellites. The full formulas for all conic sections are also provided.How to compute area of spherical triangle given the aperture angles subtended...



How to compute area of spherical triangle given the aperture angles subtended...Harish Chandra Rajpoot
Ėý
The author Mr H.C. Rajpoot has derived the general formula to compute the area of the spherical triangle having each side as a great circle arc on the spherical surface when 1.) aperture angle subtended by each of three sides at the center of sphere are known 2.) arc length of each of three sides is known. These formula are applicable for any spherical triangle to the compute area on the sphere.Central And Inscribed Angles



Central And Inscribed AnglesRyanWatt
Ėý
The document defines and provides examples of central angles, inscribed angles, and the angles in a circle theorem. It states that a central angle is equal to twice the measure of the inscribed angle subtended by the same arc. Examples apply this theorem to find the measures of unspecified angles.Pre-Cal 40S šÝšÝßĢs May 8, 2007



Pre-Cal 40S šÝšÝßĢs May 8, 2007Darren Kuropatwa
Ėý
The document describes an ellipse with foci at (2,3) and (-2,3) where the sum of the focal radii is 6 units. It asks to use the definition of an ellipse to derive the equation of this ellipse, find the radius, and coordinates of the center of the circle. It also provides information about deriving the standard form of a hyperbola equation, finding the lengths of its transverse and conjugate axes, coordinates of vertices and foci, and equations of asymptotes to sketch the hyperbola.12 4 surface area of prisms and cylinders lesson



12 4 surface area of prisms and cylinders lessongwilson8786
Ėý
This document discusses how to find the surface area of pyramids and cones. It provides formulas for calculating the surface area of regular pyramids and right cones. For a regular pyramid, the surface area is equal to the area of the base plus half the product of the perimeter of the base and the slant height. For a right cone, the surface area is equal to the area of the circular base plus the product of the radius of the base and the slant height. The document includes examples of applying these formulas to find the surface area of different pyramids and cones.Lesson 8 conic sections - parabola



Lesson 8 conic sections - parabolaJean Leano
Ėý
The document defines conic sections and describes parabolas. It provides specific objectives related to defining conic sections, identifying different types, describing parabolas, and converting between general and standard forms of parabola equations. It then gives details on the focus, directrix, vertex, latus rectum, and eccentricity of parabolas. Examples of problems involving finding parabola equations and properties from conditions are also provided.Circle lesson



Circle lessonarvin gutierrez
Ėý
This document discusses conic sections and circles. It defines conic sections as sections obtained when a plane cuts through a circular cone. It defines a circle as the set of all points equidistant from a fixed center point, where the fixed distance is called the radius. The document also mentions that Apollonius, a Greek mathematician, studied conic sections and gave them their names. He believed they should be studied for their mathematical beauty rather than practical applications.Conic sections



Conic sectionsWalsh Jno-Baptiste
Ėý
The document describes different methods for drawing ellipses, parabolas, and hyperbolas which are known as conic sections. These curves are formed by cutting a cone with planes. Ellipses can be drawn using the concentric circle method, rectangle method, oblong method, arcs of circle method, and rhombus method. Examples are given demonstrating how to draw ellipses using each of these techniques. Parabolas and hyperbolas are also defined and their eccentricities described. Methods for drawing tangents and normals to these curves are also mentioned.How to Calculate Distances from Centerline to Inside Walls of Domes, for Any ...



How to Calculate Distances from Centerline to Inside Walls of Domes, for Any ...James Smith
Ėý
Prepared for those who build earthbag domes, and need to know the distance from centerline to inside wall as a function of height above ground.Math slide area and volume 



Math slide area and volume christinelee1996
Ėý
This document discusses cones, frustums, and their properties. It defines a cone as having a circular base and curved side ending at an apex or vertex. A frustum is formed by cutting off the tip of a cone with a cut perpendicular to its height, leaving upper and lower circular bases. The document provides formulas for calculating the volume and surface area of cones and frustums. It gives examples of applying these formulas to solve problems involving cones and frustums.Involutes



InvolutesKhushwant_Jain
Ėý
This document discusses involutes and how they relate to gear teeth. It provides the following key points:
1) An involute is a curve traced by a point on a taut cord unwinding from a circle or polygon. It becomes straighter as it unwinds and is straighter for larger base circles.
2) The teeth of gears have the shape of an involute curve. This ensures the relative rotation speeds of mating gears remains constant while engaged, preventing vibration and wear.
3) Steps are provided to draw the involute curve for different basic shapes including a straight line, triangle, square, hexagon, circle, and half circle/hexagon combination.Curves in Engineering



Curves in EngineeringRathnavel Ponnuswami
Ėý
The document discusses various types of curves that are important in engineering applications. It covers conic sections like ellipses, parabolas and hyperbolas. It also discusses roulettes like cycloids and trochoids that are generated by a point on a moving circle. Involutes, which are curves traced by a point unwinding from a circle, are also covered. Examples are provided of how these curves are used in civil, mechanical and electrical engineering applications.Conic Sections



Conic SectionsRoberto Discutido
Ėý
Conics are plane curves formed by cutting a double right circular cone with a plane. The type of conic section depends on the angle of the cutting plane to the cone's axis: a circle for perpendicular, ellipse for non-perpendicular, parabola for parallel to the edge, and hyperbola for intersecting both cones. A parabola is the set of points equidistant from a focus point and directrix line, with the vertex halfway between them. The latus rectum connects the endpoints equidistant from the focus, determining how wide the parabola opens. The four types of parabolas depend on the axis and opening direction.Pre-Cal 40S šÝšÝßĢs December 18, 2007



Pre-Cal 40S šÝšÝßĢs December 18, 2007Darren Kuropatwa
Ėý
The document provides instructions to (i) write ellipses in standard form, (ii) determine the lengths of the major and minor axes, coordinates of vertices and foci, and (iii) sketch graphs of ellipses. It also gives the foci of an ellipse as F1(2,3) and F2(-2,3) and says the sum of focal radii is 6 units, instructing the reader to use this information to derive the equation of this ellipse and find the radius and coordinates of the center.Circles PPT



Circles PPTsiddhants4000
Ėý
The document discusses the properties and history of circles. It defines a circle as a set of points equidistant from a center point. Some key facts:
- Circles have been known since prehistory and are the basis for inventions like wheels.
- Euclid extensively studied circles' properties in his Elements around 300 BCE.
- The document lists many circle theorems and applications, such as using circles for gears, balls, Ferris wheels and charts.
- It provides interesting circle facts and concludes that circles play an important role in life.ellipse



ellipsekanikab1
Ėý
An ellipse is a closed curve where the sum of the distances from two fixed points (foci) to any point on the curve is a constant. It can be defined parametrically using angles or implicitly as a second-degree equation. Key properties include the major and minor axes, which are lines of symmetry, and the eccentricity, which is a measure of how non-circular the ellipse is. The area of an ellipse is Ïab and its circumference can be calculated using elliptic integrals.Sol72



Sol72eli priyatna laidan
Ėý
The document provides methods for finding the foci of ellipses, parabolas, and hyperbolas based on their geometric properties:
1) For ellipses, the center is found by bisecting chords between parallel lines intersecting the ellipse, and the major and minor axes are used to locate the foci on the major axis.
2) For parabolas, the axis is found by bisecting chords between parallel lines, and the focus lies where lines through the vertex intersecting the parabola meet the axis.
3) For hyperbolas, the center is found analytically as the intersection of lines containing midpoints of parallel chords, and the foci lie at aCircles IX



Circles IXVaibhav Goel
Ėý
Vaibhav Goel presented on circles and their properties. The presentation included definitions of key circle terms like radius, diameter, chord, and arc. It also proved several theorems: equal chords subtend equal angles at the center; a perpendicular from the center bisects a chord; there is one circle through three non-collinear points; equal chords are equidistant from the center; congruent arcs subtend equal angles; and the angle an arc subtends at the center is double that at any other point. The presentation concluded that angles in the same segment are equal and cyclic quadrilaterals have opposite angles summing to 180 degrees.INTRODUCTION TO CONIC SECTIONS (BASIC CALCULUS).pdf



INTRODUCTION TO CONIC SECTIONS (BASIC CALCULUS).pdfLyndrianShalomBaclay
Ėý
This document provides an introduction to conic sections, including circles, ellipses, parabolas, hyperbolas, and degenerate cases. It defines key terms like cones, double-napped cones, vertices, foci, directrices, and centers. Examples are given of different conic sections formed by varying the intersection of planes with double-napped cones. The common elements of conic sections are discussed and illustrated. Examples are worked through to identify the foci, vertices and directrices of parabolas based on their graphs. An assessment with questions is included to test understanding.CHG 709 - LECTURE 4.pptx



CHG 709 - LECTURE 4.pptxAmeliaEnakirerhi
Ėý
The document provides information on geometric constructions of conic sections. It defines conic sections as curves formed by the intersection of a plane and a cone, including circles, ellipses, parabolas, and hyperbolas. It then describes several methods for constructing each type of conic section geometrically, such as using concentric circles to draw an ellipse, the focus-directrix definition to draw parabolas, and locus properties involving distances from two focal points to draw hyperbolas. Diagrams illustrate each construction method.Plano numerico o cartesiano



Plano numerico o cartesianoGabrielaAlexandraFig
Ėý
The document discusses various geometric concepts in the Cartesian coordinate plane, including:
- The Cartesian coordinate plane consists of perpendicular x and y axes intersecting at the origin point.
- Points in the plane are represented by ordered pairs (x, y).
- Distances between points can be calculated using the distances between their x and y coordinates.
- Circles, ellipses, hyperbolas, and parabolas can all be represented by equations involving x and y, with their key elements like foci, vertices, axes defined in terms of coordinates.
- Examples are given of finding the equations of circles, ellipses, hyperbolas, and parabolas given information about their geometric properties.More Related Content
What's hot (19)
Applications of conic sections3



Applications of conic sections3Iram Khan
Ėý
This document discusses applications of various conic sections in real life. It begins by defining conic sections as curves derived from slicing a double-napped cone and lists the main types - parabolas, ellipses, circles, and hyperbolas. It then provides examples of applications for each type of conic section, such as parabolas in football trajectories, ellipses in eye shapes and planet orbits, circles in wheels and records, and hyperbolas in sonic booms and lighthouse beams. The document aims to illustrate how conic sections appear frequently in architecture, engineering, and natural phenomena.Conic section



Conic sectionAaryanMaheshwari
Ėý
This document discusses the four types of conic sections: circles, parabolas, ellipses, and hyperbolas. Each conic section is defined by its geometric properties and standard equation. Examples are given of real-life applications of each conic section, such as circles used in giant wheels and parabolas used in bridges and satellites. The full formulas for all conic sections are also provided.How to compute area of spherical triangle given the aperture angles subtended...



How to compute area of spherical triangle given the aperture angles subtended...Harish Chandra Rajpoot
Ėý
The author Mr H.C. Rajpoot has derived the general formula to compute the area of the spherical triangle having each side as a great circle arc on the spherical surface when 1.) aperture angle subtended by each of three sides at the center of sphere are known 2.) arc length of each of three sides is known. These formula are applicable for any spherical triangle to the compute area on the sphere.Central And Inscribed Angles



Central And Inscribed AnglesRyanWatt
Ėý
The document defines and provides examples of central angles, inscribed angles, and the angles in a circle theorem. It states that a central angle is equal to twice the measure of the inscribed angle subtended by the same arc. Examples apply this theorem to find the measures of unspecified angles.Pre-Cal 40S šÝšÝßĢs May 8, 2007



Pre-Cal 40S šÝšÝßĢs May 8, 2007Darren Kuropatwa
Ėý
The document describes an ellipse with foci at (2,3) and (-2,3) where the sum of the focal radii is 6 units. It asks to use the definition of an ellipse to derive the equation of this ellipse, find the radius, and coordinates of the center of the circle. It also provides information about deriving the standard form of a hyperbola equation, finding the lengths of its transverse and conjugate axes, coordinates of vertices and foci, and equations of asymptotes to sketch the hyperbola.12 4 surface area of prisms and cylinders lesson



12 4 surface area of prisms and cylinders lessongwilson8786
Ėý
This document discusses how to find the surface area of pyramids and cones. It provides formulas for calculating the surface area of regular pyramids and right cones. For a regular pyramid, the surface area is equal to the area of the base plus half the product of the perimeter of the base and the slant height. For a right cone, the surface area is equal to the area of the circular base plus the product of the radius of the base and the slant height. The document includes examples of applying these formulas to find the surface area of different pyramids and cones.Lesson 8 conic sections - parabola



Lesson 8 conic sections - parabolaJean Leano
Ėý
The document defines conic sections and describes parabolas. It provides specific objectives related to defining conic sections, identifying different types, describing parabolas, and converting between general and standard forms of parabola equations. It then gives details on the focus, directrix, vertex, latus rectum, and eccentricity of parabolas. Examples of problems involving finding parabola equations and properties from conditions are also provided.Circle lesson



Circle lessonarvin gutierrez
Ėý
This document discusses conic sections and circles. It defines conic sections as sections obtained when a plane cuts through a circular cone. It defines a circle as the set of all points equidistant from a fixed center point, where the fixed distance is called the radius. The document also mentions that Apollonius, a Greek mathematician, studied conic sections and gave them their names. He believed they should be studied for their mathematical beauty rather than practical applications.Conic sections



Conic sectionsWalsh Jno-Baptiste
Ėý
The document describes different methods for drawing ellipses, parabolas, and hyperbolas which are known as conic sections. These curves are formed by cutting a cone with planes. Ellipses can be drawn using the concentric circle method, rectangle method, oblong method, arcs of circle method, and rhombus method. Examples are given demonstrating how to draw ellipses using each of these techniques. Parabolas and hyperbolas are also defined and their eccentricities described. Methods for drawing tangents and normals to these curves are also mentioned.How to Calculate Distances from Centerline to Inside Walls of Domes, for Any ...



How to Calculate Distances from Centerline to Inside Walls of Domes, for Any ...James Smith
Ėý
Prepared for those who build earthbag domes, and need to know the distance from centerline to inside wall as a function of height above ground.Math slide area and volume 



Math slide area and volume christinelee1996
Ėý
This document discusses cones, frustums, and their properties. It defines a cone as having a circular base and curved side ending at an apex or vertex. A frustum is formed by cutting off the tip of a cone with a cut perpendicular to its height, leaving upper and lower circular bases. The document provides formulas for calculating the volume and surface area of cones and frustums. It gives examples of applying these formulas to solve problems involving cones and frustums.Involutes



InvolutesKhushwant_Jain
Ėý
This document discusses involutes and how they relate to gear teeth. It provides the following key points:
1) An involute is a curve traced by a point on a taut cord unwinding from a circle or polygon. It becomes straighter as it unwinds and is straighter for larger base circles.
2) The teeth of gears have the shape of an involute curve. This ensures the relative rotation speeds of mating gears remains constant while engaged, preventing vibration and wear.
3) Steps are provided to draw the involute curve for different basic shapes including a straight line, triangle, square, hexagon, circle, and half circle/hexagon combination.Curves in Engineering



Curves in EngineeringRathnavel Ponnuswami
Ėý
The document discusses various types of curves that are important in engineering applications. It covers conic sections like ellipses, parabolas and hyperbolas. It also discusses roulettes like cycloids and trochoids that are generated by a point on a moving circle. Involutes, which are curves traced by a point unwinding from a circle, are also covered. Examples are provided of how these curves are used in civil, mechanical and electrical engineering applications.Conic Sections



Conic SectionsRoberto Discutido
Ėý
Conics are plane curves formed by cutting a double right circular cone with a plane. The type of conic section depends on the angle of the cutting plane to the cone's axis: a circle for perpendicular, ellipse for non-perpendicular, parabola for parallel to the edge, and hyperbola for intersecting both cones. A parabola is the set of points equidistant from a focus point and directrix line, with the vertex halfway between them. The latus rectum connects the endpoints equidistant from the focus, determining how wide the parabola opens. The four types of parabolas depend on the axis and opening direction.Pre-Cal 40S šÝšÝßĢs December 18, 2007



Pre-Cal 40S šÝšÝßĢs December 18, 2007Darren Kuropatwa
Ėý
The document provides instructions to (i) write ellipses in standard form, (ii) determine the lengths of the major and minor axes, coordinates of vertices and foci, and (iii) sketch graphs of ellipses. It also gives the foci of an ellipse as F1(2,3) and F2(-2,3) and says the sum of focal radii is 6 units, instructing the reader to use this information to derive the equation of this ellipse and find the radius and coordinates of the center.Circles PPT



Circles PPTsiddhants4000
Ėý
The document discusses the properties and history of circles. It defines a circle as a set of points equidistant from a center point. Some key facts:
- Circles have been known since prehistory and are the basis for inventions like wheels.
- Euclid extensively studied circles' properties in his Elements around 300 BCE.
- The document lists many circle theorems and applications, such as using circles for gears, balls, Ferris wheels and charts.
- It provides interesting circle facts and concludes that circles play an important role in life.ellipse



ellipsekanikab1
Ėý
An ellipse is a closed curve where the sum of the distances from two fixed points (foci) to any point on the curve is a constant. It can be defined parametrically using angles or implicitly as a second-degree equation. Key properties include the major and minor axes, which are lines of symmetry, and the eccentricity, which is a measure of how non-circular the ellipse is. The area of an ellipse is Ïab and its circumference can be calculated using elliptic integrals.Sol72



Sol72eli priyatna laidan
Ėý
The document provides methods for finding the foci of ellipses, parabolas, and hyperbolas based on their geometric properties:
1) For ellipses, the center is found by bisecting chords between parallel lines intersecting the ellipse, and the major and minor axes are used to locate the foci on the major axis.
2) For parabolas, the axis is found by bisecting chords between parallel lines, and the focus lies where lines through the vertex intersecting the parabola meet the axis.
3) For hyperbolas, the center is found analytically as the intersection of lines containing midpoints of parallel chords, and the foci lie at aCircles IX



Circles IXVaibhav Goel
Ėý
Vaibhav Goel presented on circles and their properties. The presentation included definitions of key circle terms like radius, diameter, chord, and arc. It also proved several theorems: equal chords subtend equal angles at the center; a perpendicular from the center bisects a chord; there is one circle through three non-collinear points; equal chords are equidistant from the center; congruent arcs subtend equal angles; and the angle an arc subtends at the center is double that at any other point. The presentation concluded that angles in the same segment are equal and cyclic quadrilaterals have opposite angles summing to 180 degrees.How to compute area of spherical triangle given the aperture angles subtended...



How to compute area of spherical triangle given the aperture angles subtended...Harish Chandra Rajpoot
Ėý
Similar to Conic section (20)
INTRODUCTION TO CONIC SECTIONS (BASIC CALCULUS).pdf



INTRODUCTION TO CONIC SECTIONS (BASIC CALCULUS).pdfLyndrianShalomBaclay
Ėý
This document provides an introduction to conic sections, including circles, ellipses, parabolas, hyperbolas, and degenerate cases. It defines key terms like cones, double-napped cones, vertices, foci, directrices, and centers. Examples are given of different conic sections formed by varying the intersection of planes with double-napped cones. The common elements of conic sections are discussed and illustrated. Examples are worked through to identify the foci, vertices and directrices of parabolas based on their graphs. An assessment with questions is included to test understanding.CHG 709 - LECTURE 4.pptx



CHG 709 - LECTURE 4.pptxAmeliaEnakirerhi
Ėý
The document provides information on geometric constructions of conic sections. It defines conic sections as curves formed by the intersection of a plane and a cone, including circles, ellipses, parabolas, and hyperbolas. It then describes several methods for constructing each type of conic section geometrically, such as using concentric circles to draw an ellipse, the focus-directrix definition to draw parabolas, and locus properties involving distances from two focal points to draw hyperbolas. Diagrams illustrate each construction method.Plano numerico o cartesiano



Plano numerico o cartesianoGabrielaAlexandraFig
Ėý
The document discusses various geometric concepts in the Cartesian coordinate plane, including:
- The Cartesian coordinate plane consists of perpendicular x and y axes intersecting at the origin point.
- Points in the plane are represented by ordered pairs (x, y).
- Distances between points can be calculated using the distances between their x and y coordinates.
- Circles, ellipses, hyperbolas, and parabolas can all be represented by equations involving x and y, with their key elements like foci, vertices, axes defined in terms of coordinates.
- Examples are given of finding the equations of circles, ellipses, hyperbolas, and parabolas given information about their geometric properties.CHAPTER -10 CIRCLE 9TH CLASS NCERT 



CHAPTER -10 CIRCLE 9TH CLASS NCERT anzarshah43
Ėý
The document defines key terms related to circles such as radius, diameter, chord, arc, and sector. It discusses properties of circles including: angles subtended by chords; perpendiculars from the center to chords bisect chords; there is one unique circle through three non-collinear points; equal chords are equidistant from the center; congruent arcs subtend equal angles; and the sums of opposite angles in a cyclic quadrilateral are 180 degrees. The document concludes by summarizing key properties of circles.Bhoomi Popli...11-D...09.. Maths.pptx



Bhoomi Popli...11-D...09.. Maths.pptxjogindersikka1
Ėý
The document is an art integration project submitted by Bhoomi Popli to their mathematics teacher Mr. RP Gupta. It discusses the different conic sections formed by cutting a cone with a plane, including circles, ellipses, parabolas, and hyperbolas. For each conic section, it provides the standard mathematical definition and the simplest form of the equation when oriented in specific ways.Actividad colaborativa 551108 20



Actividad colaborativa 551108 20CarmenElisaRiosDiaz
Ėý
This document provides information about ellipses, hyperbolas, parabolas, and circles. It defines key elements of each curve such as foci, vertices, axes, and directrix. It also presents the standard equation for each curve in both canonical form (centered at the origin) and general form (shifted center). Examples are given of shifting the coordinates to obtain equations for non-canonical curves.Presentationkdkdbzbzkbzbdjxjxhdjdhhdjxhdjdj



Presentationkdkdbzbzkbzbdjxjxhdjdhhdjxhdjdjkrllpds
Ėý
msnsnshsnskzhzksizhzkdjxbxkxjdhdkxjdbdnjdbdndkdjdbdkdjjdCONIC SECTIONS.pptx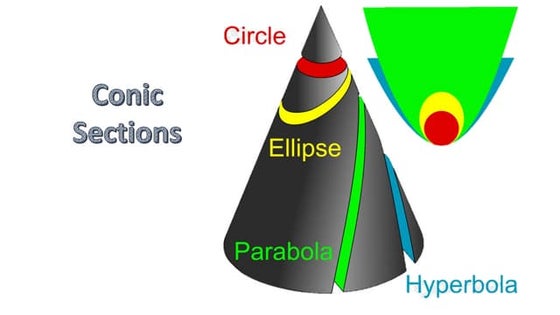



CONIC SECTIONS.pptxRuelDadivasLicanto
Ėý
The document discusses different types of conic sections formed by the intersection of a plane and a cone. It defines conic sections as circles, parabolas, ellipses, hyperbolas, and degenerate cases. It provides details on the characteristics of each conic section, describing how the angle of the intersecting plane determines whether a circle, ellipse, parabola, or hyperbola is formed. Degenerate conic sections are also defined, which can be a point, line, or two intersecting lines depending on the angle of the plane.Plano numÃĐrico



Plano numÃĐricoAngelyMichelleAmaroG
Ėý
The document discusses various geometric concepts related to coordinate planes and conic sections including:
- The Cartesian coordinate plane is formed from two perpendicular lines called the x and y axes.
- Points on the plane are located using an ordered pair (x,y) coordinate.
- The distance between two points can be calculated from their coordinate differences.
- Examples of conic sections like circles, parabolas, ellipses and hyperbolas are explained in terms of their geometric properties and equations.
- An example problem demonstrates how to derive the equation of a hyperbola given information about its foci.Conic Sections



Conic SectionsJasminJoyceTerrado
Ėý
The conic sections are the nondegenerate curves generated by the intersections of a plane with one or two nappes of a cone.1-ELLIPSE.pptx



1-ELLIPSE.pptxJohannPaulusRobles
Ėý
The Kaybiang Tunnel is the longest elliptical shaped tunnel in the Philippines, connecting two towns. An ellipse is the set of all points in a plane where the sum of the distances from two fixed points, called foci, is a constant. The Kaybiang Tunnel has an elliptical shape with its longest section piercing through a mountain.Precal 3-4.pptx



Precal 3-4.pptxjamesvalenzuela6
Ėý
This document provides information about ellipses and hyperbolas. It defines ellipses as sets of points where the sum of the distances to two fixed foci is a constant. Hyperbolas are defined as sets of points where the difference of distances to two foci is a constant. The document gives equations and properties of ellipses and hyperbolas like foci, vertices, axes, asymptotes. It includes examples of finding standard forms of equations and graphing ellipses and hyperbolas given properties.Lesson 9 conic sections - ellipse



Lesson 9 conic sections - ellipseJean Leano
Ėý
An ellipse is defined as the set of all points where the sum of the distances from two fixed points (foci) is a constant (the length of the major axis). Key properties include:
- The vertices are the endpoints of the major axis.
- The distance from the center to each focus is the eccentricity.
- The general equation of an ellipse with center at (h,k) is (x-h)^2/a^2 + (y-k)^2/b^2 = 1.
- Examples are provided to illustrate finding the equation of an ellipse given properties like the foci, vertices, or axes.Pre Calculus - Introduction to the Conic Section :Ellipse



Pre Calculus - Introduction to the Conic Section :EllipseGene95739
Ėý
The document defines an ellipse and its key properties:
1) An ellipse is a set of points whose sum of distances from two fixed foci is constant.
2) The major and minor axes, foci, latera recta, directrices and center are properties of an ellipse.
3) The learning objectives are to define an ellipse, graph it, determine its standard equation, and identify its properties from a given equation.Maths Circle PPT Class10



Maths Circle PPT Class10Abhey Gupta
Ėý
This document summarizes key terms and theorems related to circles:
1. It defines circles and related terms like radius, diameter, chord, arc, and sector.
2. It describes theorems like equal chords subtend equal angles at the center, and conversely if angles are equal then chords are equal.
3. Other concepts covered include perpendiculars from the center bisect chords, congruent arcs subtend equal angles, and cyclic quadrilaterals have opposite angles summing to 180 degrees.Circles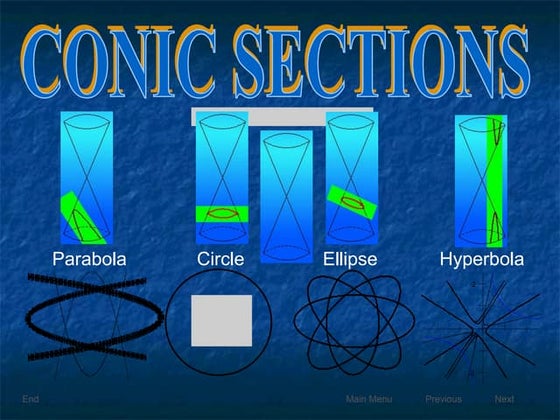



CirclesJessica Garcia
Ėý
Conics are curves formed by the intersection of a plane with a double cone. A hyperbola results if the plane cuts both cones, a parabola if the plane is parallel to the edge of the cone, and an ellipse if neither of those cases apply. A circle is a special type of ellipse that occurs when the plane is perpendicular to the altitude of the cone.Unidad 3 paso4pensamiento geomÃĐtrico y analitico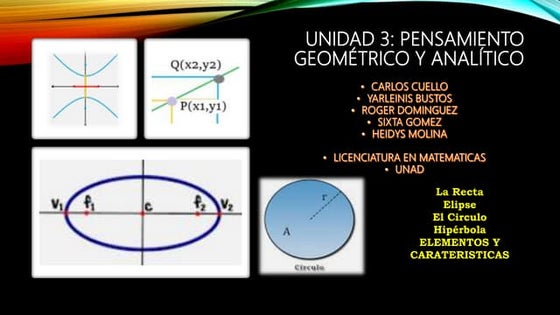



Unidad 3 paso4pensamiento geomÃĐtrico y analiticorogerstevedominguezm
Ėý
PresentaciÃģn de caracterÃsticas de los elementos y temÃĄticas de la Unidad 3: Pensamiento GeomÃĐtrico y AnalÃticoCase study on circles



Case study on circlesSanjith Varun Rajendran
Ėý
This document summarizes key concepts about circles. It defines circles and related terms like radius, diameter, chord, arc, and sector. It presents 8 theorems about angles subtended by chords and arcs, perpendiculars from the center to chords, circles through 3 points, equal chords and their distances from the center, and cyclic quadrilaterals. The concluding section summarizes that equal chords and arcs have corresponding relationships, angles in the same segment are equal, and properties of cyclic quadrilaterals. The document provides definitions, proofs, and conclusions about geometric properties of circles.Pensamiento geometrico analitico



Pensamiento geometrico analiticoYennyCarolinaMuozHor
Ėý
This document discusses conic sections, which are curves formed by the intersection of a plane and a cone. There are four types of conic sections: circles, ellipses, parabolas, and hyperbolas. Each conic section can be defined geometrically. For example, a circle is formed when the intersecting plane is perpendicular to the cone's axis of revolution. All conic sections can be represented by a second-degree equation, with some coefficient being non-zero to distinguish the different types of curves.Circles



Circleskunnalcoolguy
Ėý
1. The document defines key terms related to circles such as diameter, radius, chord, arc, and sector.
2. Several theorems about circles are presented, including that equal chords of a circle subtend equal angles at the center, and the perpendicular from the center of a circle to a chord bisects the chord.
3. The document summarizes that a circle can be defined as all points equidistant from a fixed point, and introduces various properties and relationships regarding angles, chords, and points on circles.More from Mxolisi Creswell MNCUBE (7)
Grade 10 acids and bases



Grade 10 acids and basesMxolisi Creswell MNCUBE
Ėý
The definition of Acids and Bases based on Bronsted-Lowery Model. It describes the fundamental properties of both the acids and the bases.Matter and materials



Matter and materialsMxolisi Creswell MNCUBE
Ėý
1. The document discusses various properties of matter and how they are used to classify and identify different types of matter. It describes extensive properties that depend on amount and intensive properties that depend on type.
2. Mixtures and pure substances are introduced. Heterogeneous mixtures are non-uniform while homogeneous mixtures are uniform throughout. Elements have a unique set of properties while compounds contain two or more elements.
3. The three states of matter are defined as solid, liquid, and gas. Physical and chemical changes are distinguished based on whether the composition changes. Chemical symbols and formulas are used to represent elements and compounds in chemical reactions.Matter and materials 2



Matter and materials 2Mxolisi Creswell MNCUBE
Ėý
1. Matter is everything that has mass and takes up space, and is composed of atoms. There are three main states of matter: solids, liquids, and gases.
2. Solids have a definite shape and volume, with molecules close together. Liquids take the shape of their container but maintain a constant volume. Gases fill their container and have no definite shape or volume.
3. Physical properties can be observed without changing the identity of the substance, such as density, melting point, and boiling point. Changes in state are physical changes. Chemical changes alter the chemical composition.Four spheres



Four spheresMxolisi Creswell MNCUBE
Ėý
This document describes the four spheres that make up Earth's systems - the hydrosphere, atmosphere, geosphere, and biosphere. It provides details on each sphere, including that the hydrosphere is made up of 71% of Earth's surface as oceans and saltwater, while the atmosphere is a thin gaseous envelope composed of nitrogen, oxygen, water vapor and aerosols. The document also notes that the geosphere encompasses Earth's solid interior from the crust to the core, and the biosphere incorporates all living things on the planet.Euclidean geometry grade 11



Euclidean geometry grade 11Mxolisi Creswell MNCUBE
Ėý
This document discusses various topics in Euclidean geometry for Grade 10 including angles, triangles, congruency, similarity, Pythagoras' theorem, quadrilaterals, parallelograms, rectangles, rhombuses, squares, trapezoids, kites, and the mid-point theorem. It provides definitions and properties for each shape. The mid-point theorem states that the line joining the mid-points of two sides of a triangle is parallel to the third side and equal to half its length.Analytic geometry basic concepts



Analytic geometry basic conceptsMxolisi Creswell MNCUBE
Ėý
This document provides basic concepts of analytic geometry for grades 10-12. It discusses how analytic geometry uses algebraic equations to describe geometric figures on a coordinate system, and how Rene Descartes and Pierre de Fermat independently developed its foundations in the 1630s. It also defines key concepts like the Cartesian plane, coordinates, slope, distance and midpoint formulas, and angle formulas for lines.Projectile motion



Projectile motionMxolisi Creswell MNCUBE
Ėý
This document discusses projectile motion, including:
- Projectiles are objects in free motion under the influence of gravity and potentially air resistance.
- Projectile motion can be analyzed by separating the horizontal and vertical components.
- The trajectory of a projectile in the absence of air resistance is parabolic.
- Problems can be solved by considering the horizontal and vertical motions separately using kinematic equations and conservation of energy as appropriate.
- Maximum height and range depend on the launch angle and initial velocity.Recently uploaded (20)
How to create security group category in Odoo 17



How to create security group category in Odoo 17Celine George
Ėý
This slide will represent the creation of security group category in odoo 17. Security groups are essential for managing user access and permissions across different modules. Creating a security group category helps to organize related user groups and streamline permission settings within a specific module or functionality.Dot NET Core Interview Questions PDF By ScholarHat



Dot NET Core Interview Questions PDF By ScholarHatScholarhat
Ėý
Dot NET Core Interview Questions PDF By ScholarHatOne Click RFQ Cancellation in Odoo 18 - Odoo šÝšÝßĢs



One Click RFQ Cancellation in Odoo 18 - Odoo šÝšÝßĢsCeline George
Ėý
In this slide, weâll discuss the one click RFQ Cancellation in odoo 18. One-Click RFQ Cancellation in Odoo 18 is a feature that allows users to quickly and easily cancel Request for Quotations (RFQs) with a single click.ASP.NET Web API Interview Questions By Scholarhat



ASP.NET Web API Interview Questions By ScholarhatScholarhat
Ėý
ASP.NET Web API Interview Questions By ScholarhatMeeting the needs of modern students?, Selina McCoy



Meeting the needs of modern students?, Selina McCoyEconomic and Social Research Institute
Ėý
NAPD Annual Symposium
âEquity in our Schools: Does the system deliver for all young people?âEntity Framework Interview Questions PDF By ScholarHat



Entity Framework Interview Questions PDF By ScholarHatScholarhat
Ėý
Entity Framework Interview Questions PDF By ScholarHatAdministrative bodies( D and C Act, 1940



Administrative bodies( D and C Act, 1940P.N.DESHMUKH
Ėý
These presentation include information about administrative bodies such as D.T.A.B
CDL AND DCC, etc.Interim Guidelines for PMES-DM-17-2025-PPT.pptx



Interim Guidelines for PMES-DM-17-2025-PPT.pptxsirjeromemanansala
Ėý
This is the latest issuance on PMES as replacement of RPMS. Kindly message me to gain full access of the presentation. Oral exam Kenneth Bech - What is the meaning of strategic fit?



Oral exam Kenneth Bech - What is the meaning of strategic fit?MIPLM
Ėý
Presentation of the CEIPI DU IPBA oral exam of Kenneth Bech - What is the meaning of strategic fit? How to Configure Deliver Content by Email in Odoo 18 Sales



How to Configure Deliver Content by Email in Odoo 18 SalesCeline George
Ėý
In this slide, weâll discuss on how to configure proforma invoice in Odoo 18 Sales module. A proforma invoice is a preliminary invoice that serves as a commercial document issued by a seller to a buyer.Inventory Reporting in Odoo 17 - Odoo 17 Inventory App



Inventory Reporting in Odoo 17 - Odoo 17 Inventory AppCeline George
Ėý
This slide will helps us to efficiently create detailed reports of different records defined in its modules, both analytical and quantitative, with Odoo 17 ERP.Full-Stack .NET Developer Interview Questions PDF By ScholarHat



Full-Stack .NET Developer Interview Questions PDF By ScholarHatScholarhat
Ėý
Full-Stack .NET Developer Interview Questions PDF By ScholarHatMastering Soft Tissue Therapy & Sports Taping



Mastering Soft Tissue Therapy & Sports TapingKusal Goonewardena
Ėý
Mastering Soft Tissue Therapy & Sports Taping: Pathway to Sports Medicine Excellence
This presentation was delivered in Colombo, Sri Lanka, at the Institute of Sports Medicine to an audience of sports physiotherapists, exercise scientists, athletic trainers, and healthcare professionals. Led by Kusal Goonewardena (PhD Candidate - Muscle Fatigue, APA Titled Sports & Exercise Physiotherapist) and Gayath Jayasinghe (Sports Scientist), the session provided comprehensive training on soft tissue assessment, treatment techniques, and essential sports taping methods.
Key topics covered:
â
Soft Tissue Therapy â The science behind muscle, fascia, and joint assessment for optimal treatment outcomes.
â
Sports Taping Techniques â Practical applications for injury prevention and rehabilitation, including ankle, knee, shoulder, thoracic, and cervical spine taping.
â
Sports Trainer Level 1 Course by Sports Medicine Australia â A gateway to professional development, career opportunities, and working in Australia.
This training mirrors the Elite Akademy Sports Medicine standards, ensuring evidence-based approaches to injury management and athlete care.
If you are a sports professional looking to enhance your clinical skills and open doors to global opportunities, this presentation is for you.Conic section
- 1. CONIC SECTION MATH-002 Dr. Farhana Shaheen
- 2. CONIC SECTION ï In mathematics, a conic section (or just conic) is a curve obtained by intersecting a cone (more precisely, a right circular conical surface) with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2. It can be defined as the locus of points whose distances are in a fixed ratio to some point, called a focus, and some line, called a directrix.
- 3. CONICS ï The three conic sections that are created when a double cone is intersected with a plane. ï 1) Parabola ï 2) Circle and ellipse ï 3) Hyperbola
- 4. CIRCLES ï A circle is a simple shape of Euclidean geometry consisting of the set of points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius.
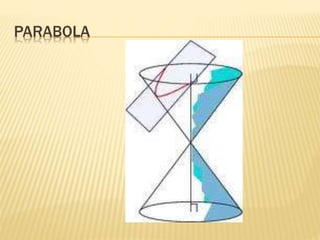
- 5. PARABOLA
- 6. PARABOLA: LOCUS OF ALL POINTS WHOSE DISTANCE FROM A FIXED POINT IS EQUAL TO THE DISTANCE FROM A FIXED LINE. THE FIXED POINT IS CALLED FOCUS AND THE FIXED LINE IS CALLED A DIRECTRIX. P(x,y)
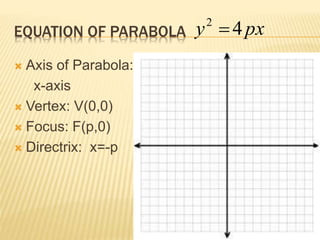
- 7. EQUATION OF PARABOLA ï Axis of Parabola: x-axis ï Vertex: V(0,0) ï Focus: F(p,0) ï Directrix: x=-p pxy 42 ï―
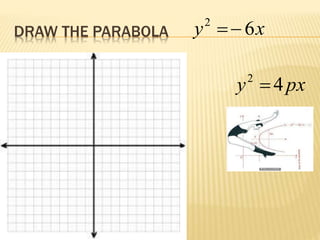
- 8. DRAW THE PARABOLA xy 62 ïï― pxy 42 ï―
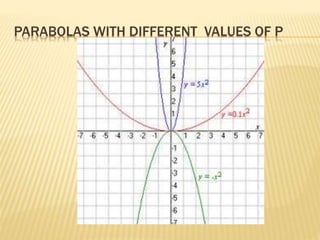
- 9. PARABOLAS WITH DIFFERENT VALUES OF P
- 10. EQUATION OF THE GIVEN PARABOLA?
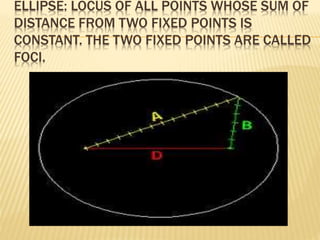
- 13. ELLIPSE: LOCUS OF ALL POINTS WHOSE SUM OF DISTANCE FROM TWO FIXED POINTS IS CONSTANT. THE TWO FIXED POINTS ARE CALLED FOCI.
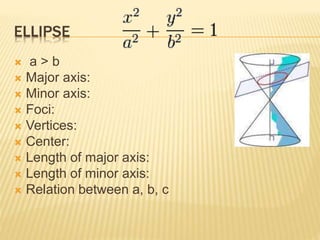
- 14. ELLIPSE ï a > b ï Major axis: ï Minor axis: ï Foci: ï Vertices: ï Center: ï Length of major axis: ï Length of minor axis: ï Relation between a, b, c
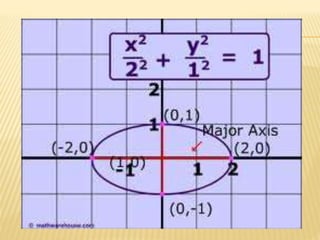
- 16. EQUATION OF THE GIVEN ELLIPSE?
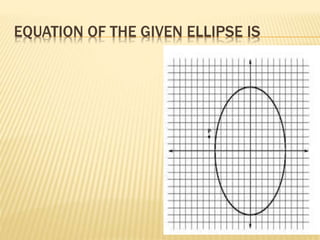
- 17. EQUATION OF THE GIVEN ELLIPSE IS
- 18. EARTH MOVES AROUND THE SUN ELLIPTICALLY
- 19. DRAW THE ELLIPSE WITH CENTER AT(H,K)
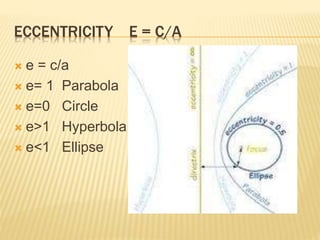
- 20. ECCENTRICITY
- 21. ECCENTRICITY IN CONIC SECTIONS ï Conic sections are exactly those curves that, for a point F, a line L not containing F and a non-negative number e, are the locus of points whose distance to F equals e times their distance to L. F is called the focus, L the directrix, and e the eccentricity.
- 22. CIRCLE AS ELLIPSE ï A circle is a special ellipse in which the two foci are coincident and the eccentricity is 0. Circles are conic sections attained when a right circular cone is intersected by a plane perpendicular to the axis of the cone.
- 23. HYPERBOLA
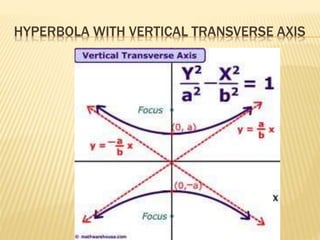
- 24. HYPERBOLA ï Transverse axis: ï Conjugate axis: ï Foci: ï Vertices: ï Center: ï Relation between a, b, c
- 25. HYPERBOLA WITH VERTICAL TRANSVERSE AXIS
- 26. ECCENTRICITY E = C/A ï e = c/a ï e= 1 Parabola ï e=0 Circle ï e>1 Hyperbola ï e<1 Ellipse
- 27. ECCENTRICITY E ELLIPSE (E=1/2), PARABOLA (E=1) AND HYPERBOLA (E=2) WITH FIXED FOCUS F AND DIRECTRIX
- 28. HYPERBOLA
- 30. THANK YOU







