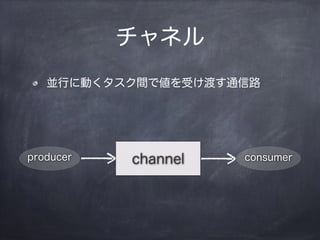
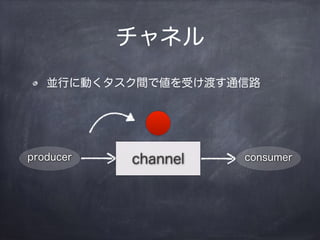
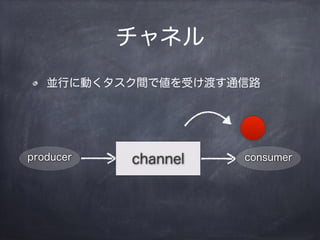
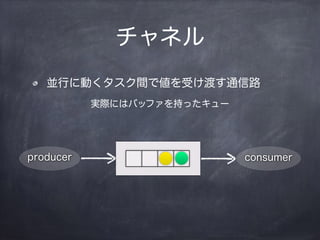
ÈëĂĆłŠŽÇ°ù±đ.ČčČőČâČÔłŠ
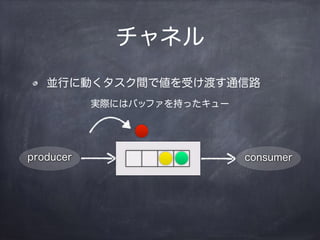
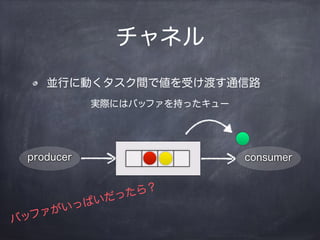
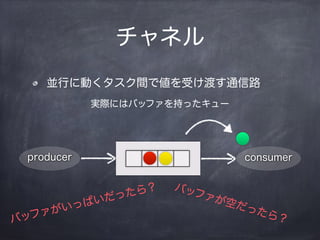
- 10. „Á„ă„Í„ë KĐĐ€ËÓ€Ż„ż„č„Żég€Ç€òÊÜ€±¶É€čÍšĐĆ· producer consumer gëH€Ë€Ï„Đ„Ă„Ő„Ą€òłÖ€Ă€ż„„ć©`
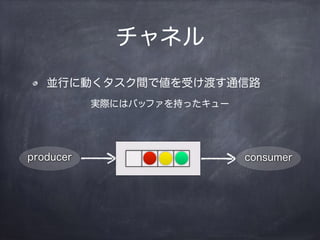
- 11. „Á„ă„Í„ë KĐĐ€ËÓ€Ż„ż„č„Żég€Ç€òÊÜ€±¶É€čÍšĐĆ· producer consumer gëH€Ë€Ï„Đ„Ă„Ő„Ą€òłÖ€Ă€ż„„ć©`
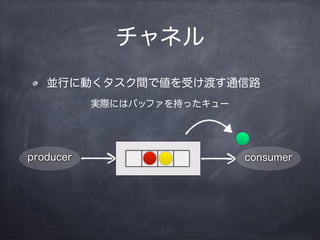
- 12. „Á„ă„Í„ë KĐĐ€ËÓ€Ż„ż„č„Żég€Ç€òÊÜ€±¶É€čÍšĐĆ· producer consumer gëH€Ë€Ï„Đ„Ă„Ő„Ą€òłÖ€Ă€ż„„ć©`
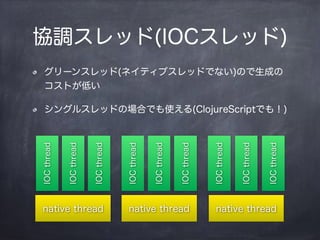
- 15. fŐ{„č„ì„Ă„É(IOC„č„ì„Ă„É) ÒÔÏ€΀耊€ÊöșÏ€ËÖÆÓù€Źe€Î„č„ì„Ă„É€ËÇĐ€êÌæ€ï€ë €òÊÜĐĆ€·€è€Š€È€·€ż€È€€Ë„Đ„Ă„Ő„Ą€ŹżŐ €òËÍĐĆ€·€è€Š€È€·€ż€È€€Ë„Đ„Ă„Ő„Ą€Ź€€€Ă€Ń€€ IOC = Inversion of Control (go (while true (let [v (<! ch)] (println v)))) (go (loop [i 0] (>! ch i) (recur (inc i))))
- 16. fŐ{„č„ì„Ă„É(IOC„č„ì„Ă„É) ÒÔÏ€΀耊€ÊöșÏ€ËÖÆÓù€Źe€Î„č„ì„Ă„É€ËÇĐ€êÌæ€ï€ë €òÊÜĐĆ€·€è€Š€È€·€ż€È€€Ë„Đ„Ă„Ő„Ą€ŹżŐ €òËÍĐĆ€·€è€Š€È€·€ż€È€€Ë„Đ„Ă„Ő„Ą€Ź€€€Ă€Ń€€ IOC = Inversion of Control (go (while true (let [v (<! ch)] (println v)))) (go (loop [i 0] (>! ch i) (recur (inc i)))) ÉÏÓ€ÎöșπˀÏ??€ŹgĐĐ€”€ì€ș€ËÖÆÓù€ŹÇĐ€êÌæ€ï€ë(„Ń©`„Ż)
- 17. fŐ{„č„ì„Ă„É(IOC„č„ì„Ă„É) „°„ê©`„ó„č„ì„Ă„É(„Í„€„Æ„Ł„Ö„č„ì„Ă„É€Ç€Ê€€)€Î€ÇÉúłÉ€Î „ł„č„È€Ź”Í€€ „·„ó„°„ë„č„ì„Ă„É€ÎöșπǀâÊ耚€ë(ClojureScript€Ç€âŁĄ) native thread native thread native thread IOCthread IOCthread IOCthread IOCthread IOCthread IOCthread IOCthread IOCthread IOCthread
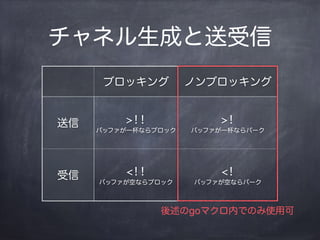
- 19. „Á„ă„Í„ëÉúłÉ€ÈËÍÊÜĐĆ „Á„ă„Í„ëÉúłÉŁșchan ËÍĐĆŁș>!, >!! ÊÜĐĆŁș<!, <!! (let [ch (chan 2)] (>!! ch 0) (>!! ch 1) [(<!! ch) (<!! ch)]) ;=> [0 1]
- 20. „Á„ă„Í„ëÉúłÉ€ÈËÍÊÜĐĆ „Á„ă„Í„ëÉúłÉŁșchan ËÍĐĆŁș>!, >!! ÊÜĐĆŁș<!, <!! (let [ch (chan 2)] (>!! ch 0) (>!! ch 1) [(<!! ch) (<!! ch)]) ;=> [0 1] „Đ„Ă„Ő„Ą€Î„”„€„ș€òÖž¶š
- 21. „Á„ă„Í„ëÉúłÉ€ÈËÍÊÜĐĆ „Ö„í„Ă„„ó„° „΄ó„Ö„í„Ă„„ó„° ËÍĐĆ >!! „Đ„Ă„Ő„Ą€ŹÒ»±€Ê€é„Ö„í„Ă„Ż >! „Đ„Ă„Ő„Ą€ŹÒ»±€Ê€é„Ń©`„Ż ÊÜĐĆ <!! „Đ„Ă„Ő„Ą€ŹżŐ€Ê€é„Ö„í„Ă„Ż <! „Đ„Ă„Ő„Ą€ŹżŐ€Ê€é„Ń©`„Ż
- 22. „Á„ă„Í„ëÉúłÉ€ÈËÍÊÜĐĆ „Ö„í„Ă„„ó„° „΄ó„Ö„í„Ă„„ó„° ËÍĐĆ >!! „Đ„Ă„Ő„Ą€ŹÒ»±€Ê€é„Ö„í„Ă„Ż >! „Đ„Ă„Ő„Ą€ŹÒ»±€Ê€é„Ń©`„Ż ÊÜĐĆ <!! „Đ„Ă„Ő„Ą€ŹżŐ€Ê€é„Ö„í„Ă„Ż <! „Đ„Ă„Ő„Ą€ŹżŐ€Ê€é„Ń©`„Ż ááÊö€Îgo„Ț„Ż„íÄڀǀ΀ßÊčÓĂżÉ
- 23. go„Ț„Ż„í fŐ{„č„ì„Ă„É€ÇIÀí€ògĐĐ€č€ë (let [ch (chan 2)] (go (while true (let [v (<! ch)] (println Ą°receivedĄ± v)))) (>!! ch Ą°hiĄ±) (>!! ch Ą°thereĄ±)) ;; received hi ;; received there
- 24. timeout (let [t (timeout 100) begin (System/currentTimeMillis)] (<!! t) (println Ą°WaitedĄ± (- (System/currentTimeMillis) begin))) ;; Waited 100 „ż„€„à„ą„Š„ÈÓÀ΄Á„ă„Í„ë€òÉúłÉ€č€ë
- 25. alts! Ò»¶È€ËŃ}Êę€Î„Á„ă„̈́뀫€éŽę€ÁÊÜ€±€ë (let [c1 (chan) c2 (chan)] (go (while true (let [[v ch] (alts! [c1 c2])] (println Ą°received" v)))) (go (>! c1 "hi")) (go (>! c2 "there"))) ;; received hi ;; received there
- 26. alts! Ò»¶È€ËŃ}Êę€Î„Á„ă„̈́뀫€éŽę€ÁÊÜ€±€ë (let [c1 (chan) c2 (chan)] (go (while true (let [[v ch] (alts! [c1 c2])] (println Ą°received" v)))) (go (>! c1 "hi")) (go (>! c2 "there"))) ;; received hi ;; received there Žę€ÁÊÜ€±€ë„Á„ă„Í„ë
- 27. alts! Ò»¶È€ËŃ}Êę€Î„Á„ă„̈́뀫€éŽę€ÁÊÜ€±€ë (let [c1 (chan) c2 (chan)] (go (while true (let [[v ch] (alts! [c1 c2])] (println Ą°received" v)))) (go (>! c1 "hi")) (go (>! c2 "there"))) ;; received hi ;; received there Žę€ÁÊÜ€±€ë„Á„ă„Í„ë ÊÜĐĆ€·€ż€ÈÊÜĐĆÔȘ€Î„Á„ă„̈́뀏·”€ë
- 28. alts! Ł« timeout ÊÜĐĆ€òŽę€ÁÊÜ€±€ërég€Ë„ż„€„à„ą„Š„È€òÔO¶š (go (let [c (chan) begin (System/currentTimeMillis)] (alts! [c (timeout 100)]) (println "Gave up afterĄ± (- (System/currentTimeMillis) begin)))
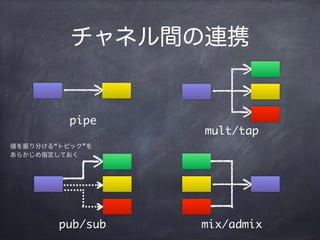
- 32. „Á„ă„Í„ëég€ÎßBĐŻ pipe mult/tap pub/sub mix/admix €òŐń€ê·Ö€±€ëĄ°„È„Ô„Ă„ŻĄ±€ò €ą€é€«€ž€áÖž¶š€·€Æ€Ș€Ż
- 34. žß„ì„Ù„ëAPI €œ€ÎËûĄąinto, merge, reduce, take ”È€ŹÓĂÒâ €”€ì€Æ€€€ë (defn split [p ch] (let [tc (chan), fc (chan)] (go (loop [] (let [v (<! ch)] (if (nil? v) (do (close! tc) (close! fc)) (when (>! (if (p v) tc fc) v) (recur)))))) [tc fc])) c.c.a/split€Î¶šÁx(Ò»ČżșÂÔ»Ż)
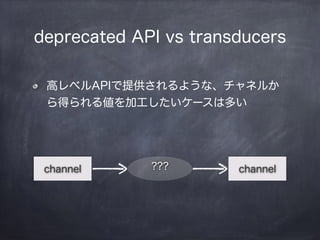
- 35. deprecated API vs transducers žß„ì„Ù„ëAPI€ÇÌáč©€”€ì€ë€è€Š€ÊĄą„Á„ă„̈́뀫 €é”Ă€é€ì€ë€òŒÓ耀·€ż€€„±©`„č€Ï¶à€€ channel ??? channel
- 36. deprecated API vs transducers core.async€Ç€Ï„Á„ă„Í„ëÓĂ€Îmap€ä?lter€âÌá č©€·€Æ€€€ż (let [ch (to-chan (range))] [(<!! ch) (<!! ch) (<!! ch)]) ;=> [0 1 2] (let [ch (->> (to-chan (range)) (map< inc) (map< #(* % %)))] [(<!! ch) (<!! ch) (<!! ch)]) ;=> [1 4 9]
- 37. deprecated API vs transducers Clojure 1.7ÒÔœ”€Ç€Ïtransducer€òÊč€Ă€ÆÍŹ€ÎIÀ퀏ű€±€ë „Á„ă„Í„ëÉúłÉr€Ëtransducer€òÖž¶š€č€ë€È„Á„ă„̈́뀫€éÈĄ”Ă €Ç€€ë€Ïtransducer€òßmÓĂ€·€żœYčû€Î€Ë€Ê€ë (let [xform (comp (map inc) (map #(* % %))) ch (pipe (to-chan (range)) (chan 1 xform))] [(<!! ch) (<!! ch) (<!! ch)]) ;=> [1 4 9] transducer




![fŐ{„č„ì„Ă„É(IOC„č„ì„Ă„É)
ÒÔÏ€΀耊€ÊöșÏ€ËÖÆÓù€Źe€Î„č„ì„Ă„É€ËÇĐ€êÌæ€ï€ë
€òÊÜĐĆ€·€è€Š€È€·€ż€È€€Ë„Đ„Ă„Ő„Ą€ŹżŐ
€òËÍĐĆ€·€è€Š€È€·€ż€È€€Ë„Đ„Ă„Ő„Ą€Ź€€€Ă€Ń€€
IOC = Inversion of Control
(go
(while true
(let [v (<! ch)]
(println v))))
(go
(loop [i 0]
(>! ch i)
(recur (inc i))))](https://image.slidesharecdn.com/coreasync-150611095123-lva1-app6891/85/core-async-15-320.jpg)
![fŐ{„č„ì„Ă„É(IOC„č„ì„Ă„É)
ÒÔÏ€΀耊€ÊöșÏ€ËÖÆÓù€Źe€Î„č„ì„Ă„É€ËÇĐ€êÌæ€ï€ë
€òÊÜĐĆ€·€è€Š€È€·€ż€È€€Ë„Đ„Ă„Ő„Ą€ŹżŐ
€òËÍĐĆ€·€è€Š€È€·€ż€È€€Ë„Đ„Ă„Ő„Ą€Ź€€€Ă€Ń€€
IOC = Inversion of Control
(go
(while true
(let [v (<! ch)]
(println v))))
(go
(loop [i 0]
(>! ch i)
(recur (inc i))))
ÉÏÓ€ÎöșπˀÏ??€ŹgĐĐ€”€ì€ș€ËÖÆÓù€ŹÇĐ€êÌæ€ï€ë(„Ń©`„Ż)](https://image.slidesharecdn.com/coreasync-150611095123-lva1-app6891/85/core-async-16-320.jpg)

![„Á„ă„Í„ëÉúłÉ€ÈËÍÊÜĐĆ
„Á„ă„Í„ëÉúłÉŁșchan
ËÍĐĆŁș>!, >!!
ÊÜĐĆŁș<!, <!!
(let [ch (chan 2)]
(>!! ch 0)
(>!! ch 1)
[(<!! ch) (<!! ch)])
;=> [0 1]](https://image.slidesharecdn.com/coreasync-150611095123-lva1-app6891/85/core-async-19-320.jpg)
![„Á„ă„Í„ëÉúłÉ€ÈËÍÊÜĐĆ
„Á„ă„Í„ëÉúłÉŁșchan
ËÍĐĆŁș>!, >!!
ÊÜĐĆŁș<!, <!!
(let [ch (chan 2)]
(>!! ch 0)
(>!! ch 1)
[(<!! ch) (<!! ch)])
;=> [0 1]
„Đ„Ă„Ő„Ą€Î„”„€„ș€òÖž¶š](https://image.slidesharecdn.com/coreasync-150611095123-lva1-app6891/85/core-async-20-320.jpg)

![go„Ț„Ż„í
fŐ{„č„ì„Ă„É€ÇIÀí€ògĐĐ€č€ë
(let [ch (chan 2)]
(go (while true
(let [v (<! ch)]
(println Ą°receivedĄ± v))))
(>!! ch Ą°hiĄ±)
(>!! ch Ą°thereĄ±))
;; received hi
;; received there](https://image.slidesharecdn.com/coreasync-150611095123-lva1-app6891/85/core-async-23-320.jpg)
![timeout
(let [t (timeout 100)
begin (System/currentTimeMillis)]
(<!! t)
(println Ą°WaitedĄ±
(- (System/currentTimeMillis)
begin)))
;; Waited 100
„ż„€„à„ą„Š„ÈÓÀ΄Á„ă„Í„ë€òÉúłÉ€č€ë](https://image.slidesharecdn.com/coreasync-150611095123-lva1-app6891/85/core-async-24-320.jpg)
![alts!
Ò»¶È€ËŃ}Êę€Î„Á„ă„̈́뀫€éŽę€ÁÊÜ€±€ë
(let [c1 (chan)
c2 (chan)]
(go (while true
(let [[v ch] (alts! [c1 c2])]
(println Ą°received" v))))
(go (>! c1 "hi"))
(go (>! c2 "there")))
;; received hi
;; received there](https://image.slidesharecdn.com/coreasync-150611095123-lva1-app6891/85/core-async-25-320.jpg)
![alts!
Ò»¶È€ËŃ}Êę€Î„Á„ă„̈́뀫€éŽę€ÁÊÜ€±€ë
(let [c1 (chan)
c2 (chan)]
(go (while true
(let [[v ch] (alts! [c1 c2])]
(println Ą°received" v))))
(go (>! c1 "hi"))
(go (>! c2 "there")))
;; received hi
;; received there
Žę€ÁÊÜ€±€ë„Á„ă„Í„ë](https://image.slidesharecdn.com/coreasync-150611095123-lva1-app6891/85/core-async-26-320.jpg)
![alts!
Ò»¶È€ËŃ}Êę€Î„Á„ă„̈́뀫€éŽę€ÁÊÜ€±€ë
(let [c1 (chan)
c2 (chan)]
(go (while true
(let [[v ch] (alts! [c1 c2])]
(println Ą°received" v))))
(go (>! c1 "hi"))
(go (>! c2 "there")))
;; received hi
;; received there
Žę€ÁÊÜ€±€ë„Á„ă„Í„ë
ÊÜĐĆ€·€ż€ÈÊÜĐĆÔȘ€Î„Á„ă„̈́뀏·”€ë](https://image.slidesharecdn.com/coreasync-150611095123-lva1-app6891/85/core-async-27-320.jpg)
![alts! Ł« timeout
ÊÜĐĆ€òŽę€ÁÊÜ€±€ërég€Ë„ż„€„à„ą„Š„È€òÔO¶š
(go
(let [c (chan)
begin (System/currentTimeMillis)]
(alts! [c (timeout 100)])
(println "Gave up afterĄ±
(- (System/currentTimeMillis)
begin)))](https://image.slidesharecdn.com/coreasync-150611095123-lva1-app6891/85/core-async-28-320.jpg)




![žß„ì„Ù„ëAPI
€œ€ÎËûĄąinto, merge, reduce, take ”È€ŹÓĂÒâ
€”€ì€Æ€€€ë
(defn split [p ch]
(let [tc (chan), fc (chan)]
(go (loop []
(let [v (<! ch)]
(if (nil? v)
(do (close! tc) (close! fc))
(when (>! (if (p v) tc fc) v)
(recur))))))
[tc fc]))
c.c.a/split€Î¶šÁx(Ò»ČżșÂÔ»Ż)](https://image.slidesharecdn.com/coreasync-150611095123-lva1-app6891/85/core-async-34-320.jpg)
![deprecated API vs transducers
core.async€Ç€Ï„Á„ă„Í„ëÓĂ€Îmap€ä?lter€âÌá
č©€·€Æ€€€ż
(let [ch (to-chan (range))]
[(<!! ch) (<!! ch) (<!! ch)])
;=> [0 1 2]
(let [ch (->> (to-chan (range))
(map< inc)
(map< #(* % %)))]
[(<!! ch) (<!! ch) (<!! ch)])
;=> [1 4 9]](https://image.slidesharecdn.com/coreasync-150611095123-lva1-app6891/85/core-async-36-320.jpg)
![deprecated API vs transducers
Clojure 1.7ÒÔœ”€Ç€Ïtransducer€òÊč€Ă€ÆÍŹ€ÎIÀ퀏ű€±€ë
„Á„ă„Í„ëÉúłÉr€Ëtransducer€òÖž¶š€č€ë€È„Á„ă„̈́뀫€éÈĄ”Ă
€Ç€€ë€Ïtransducer€òßmÓĂ€·€żœYčû€Î€Ë€Ê€ë
(let [xform (comp (map inc)
(map #(* % %)))
ch (pipe (to-chan (range))
(chan 1 xform))]
[(<!! ch) (<!! ch) (<!! ch)])
;=> [1 4 9]
transducer](https://image.slidesharecdn.com/coreasync-150611095123-lva1-app6891/85/core-async-37-320.jpg)

























































