Cube Conundrum
- 1. Cube Conundrum Unit One, Lesson One, Exploration One
- 2. from point A to point B Suppose a tiny bug desired to move along the surface of a cube from the top far corner (point A) to the near bottom corner (point B). A B
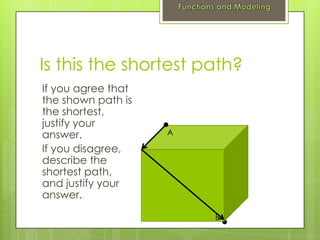
- 3. Is this the shortest path? If you agree that the shown path is the shortest, justify your answer. A If you disagree, describe the shortest path, and justify your answer. B
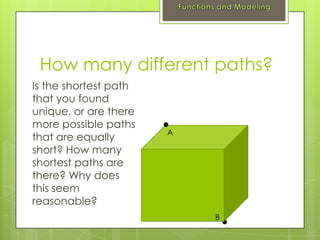
- 4. How many different paths? Is the shortest path that you found unique, or are there more possible paths A that are equally short? How many shortest paths are there? Why does this seem reasonable? B