�ݺ�ߣ

Cyclic Material Behaviour
• Stress-Strain response of most materials under
cyclic loading is different than under single
(monotonic) loading.
• For fatigue analysis, it is necessary to consider
the cyclic material behaviour for strength and
life calculations.
• Fatigue itself is a process of crack initiation
and growth due to cyclic loading.

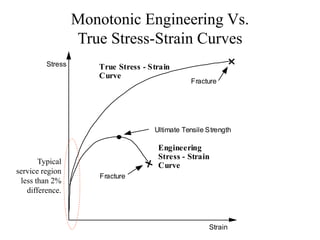
Monotonic Engineering Vs.
True Stress-Strain Curves
Stress
Strain
True Stress - Strain
Curve
Engineering
Stress - Strain
Curve
Ultimate Tensile Strength
Fracture
Fracture
Typical
service region
less than 2%
difference.

Cyclic Stress-Strain Curves
• For cyclic loading, we will always be using
true stress, s, and true strain, e.
• However, for most calculations we ignore
the difference between engineering values
(S,e) and true values (s,e):
•
0198
0
S
02
1
02
0
e
for
e
1
e
1
S
.
,
.
;
.
)
ln(
)
(







e
s
e
s

Cyclic Vs. Monotonic Stress-Strain
STRAIN
STRESS
Monotonic
Cyclic
a) SAE 1045 Steel
Quenched and
Tempered
STRAIN
STRESS
Monotonic
b) 2024-T351
Age hardened
Aluminum Alloy
Cyclic
For Steels: Su /Sys <1.2 - Cyclically Softens
Su/Sys >1.4 - Cyclically Hardens

Elastic and Plastic Strain
0.2% offset
yield stress
0.2 % STRAIN
Sy
(S )
y
E
1
E
1 E
1
STRESS
elastic
plastic
Total Strain e
ep ee
E
e
p
e
/
s
e
e
e
e



A
C

Cyclic Hysteresis Behaviour
s
e
A
B
C
D
E
F
B
C
D
E
F

More Cyclic Stress-Strain Curves

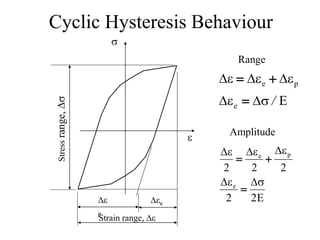
Cyclic Hysteresis Behaviour
s
e
Stress
range,
Ds
Strain range, De
De
p
Dee
E
e
p
e
/
s
D
e
D
e
D
e
D
e
D



E
2
2
2
2
2
e
p
e
s
D
e
D
e
D
e
D
e
D



Range
Amplitude

Equation for s-e Curve
'
'
n
1
p
n
p
2k'
2
2
k'
2
















s
D
e
D
e
D
s
D
n’
k’
Log(Dep/2)
Log(Ds/2)

s
e
Equation for s-e Curve
'
'
,
n
1
n
1
p
e
p
e
2k'
E
2
2
Hence
2k'
2
E
2
2
2
2
2


















s
D
s
D
e
D
s
D
e
D
s
D
e
D
e
D
e
D
e
D

Reversed Cyclic Straining
• Bauchinger Effect: After being plastically strained in
one direction the stress-strain curve of a metal in the
opposite sense is lower than the initial stress-strain
curve.
• Memory: The stress for reversed plasticity is generally
lowered because of the dislocation pile-ups and their
back stresses left by the initial straining. The stress-
strain path follows the initial path whenever the prior
maximum or minimum strain level is exceeded.
• Masing’s Hypothesis: Masing suggested (before
dislocations were observed) that the stress-strain curve
for reversed straining MEASURED FROM THE POINT
OF REVERSAL would be the cyclic curve scaled by a
factor of 2.

Bauchinger Effect
Reversed Stress-Strain Curve
Stress -Strain Curve
Stress-Strain Curve
Stress
Strain

Masing’s Hypothesis
Ds,
Ds/2
De, De/2
Cyclic
s-e curve
Reversed
s-e curve
'
'
n
1
n
1
2k'
2
E
2k'
2
E
2
2
2
2
















s
D
s
D
e
D
s
D
s
D
e
D
'
n
1
2k'
E
2
2








s
D
s
D
e
D

Memory
time
Previous reversal
point
Deformation
on previous
hysteresis loop
Material Memory
Strain
Stress
Strain

Tracking Strain Sequences
in s-e Space
• Most components subjected to cyclic loading are
susceptible to fracture by fatigue cracking and can
be monitored with strain sensors (e.g., resistance
foil strain-gauges)
• Hence, it is common to obtain service load spectra
in strain units.
• The strain data must be mapped into s-e space for
the specific material to do fatigue analysis.

Sequence Effects in Strain History

�ݺ�ߣ

Cyclic Material Behaviour, Stress-Strain

More Related Content

Cyclic Material Behaviour, Stress-Strain