DAA.pdf
- 1. P, NP, NP-Hard & NP-complete problems Prof. Shaik Naseera Department of CSE JNTUACEK, Kalikiri 1
- 2. Objectives ÔÇó P, NP, NP-Hard and NP-Complete ÔÇó Solving 3-CNF Sat problem ÔÇó Discussion of Gate Questions 2
- 3. Types of Problems ÔÇó Trackable ÔÇó Intrackable ÔÇó Decision ÔÇó Optimization 3 Trackable : Problems that can be solvable in a reasonable(polynomial) time. Intrackable : Some problems are intractable, as they grow large, we are unable to solve them in reasonable time.
- 4. Tractability ÔÇó What constitutes reasonable time? ÔÇô Standard working definition: polynomial time ÔÇô On an input of size n the worst-case running time is O(nk) for some constant k ÔÇô O(n2), O(n3), O(1), O(n lg n), O(2n), O(nn), O(n!) ÔÇô Polynomial time: O(n2), O(n3), O(1), O(n lg n) ÔÇô Not in polynomial time: O(2n), O(nn), O(n!) ÔÇó Are all problems solvable in polynomial time? ÔÇô No: TuringÔÇÖs ÔÇ£Halting ProblemÔÇØ is not solvable by any computer, no matter how much time is given. 4
- 5. Optimization/Decision Problems ÔÇó Optimization Problems ÔÇô An optimization problem is one which asks, ÔÇ£What is the optimal solution to problem X?ÔÇØ ÔÇô Examples: ÔÇó 0-1 Knapsack ÔÇó Fractional Knapsack ÔÇó Minimum Spanning Tree ÔÇó Decision Problems ÔÇô An decision problem is one with yes/no answer ÔÇô Examples: ÔÇó Does a graph G have a MST of weight ´éú W? 5
- 6. Optimization/Decision Problems ÔÇó An optimization problem tries to find an optimal solution ÔÇó A decision problem tries to answer a yes/no question ÔÇó Many problems will have decision and optimization versions ÔÇô Eg: Traveling salesman problem ÔÇó optimization: find hamiltonian cycle of minimum weight ÔÇó decision: is there a hamiltonian cycle of weight ´éú k 6
- 7. P, NP, NP-Hard, NP-Complete -Definitions 7
- 8. The Class P P: the class of problems that have polynomial-time deterministic algorithms. ÔÇô That is, they are solvable in O(p(n)), where p(n) is a polynomial on n ÔÇô A deterministic algorithm is (essentially) one that always computes the correct answer 8
- 9. Sample Problems in P ÔÇó Fractional Knapsack ÔÇó MST ÔÇó Sorting ÔÇó Others? 9
- 10. The class NP NP: the class of decision problems that are solvable in polynomial time on a nondeterministic machine (or with a nondeterministic algorithm) ÔÇô (A determinstic computer is what we know) ÔÇô A nondeterministic computer is one that can ÔÇ£guessÔÇØ the right answer or solution ÔÇó Think of a nondeterministic computer as a parallel machine that can freely spawn an infinite number of processes ÔÇó Thus NP can also be thought of as the class of problems ÔÇ£whose solutions can be verified in polynomial timeÔÇØ ÔÇó Note that NP stands for ÔÇ£Nondeterministic Polynomial-timeÔÇØ 10
- 11. Sample Problems in NP ÔÇó Fractional Knapsack ÔÇó MST ÔÇó Others? ÔÇô Traveling Salesman ÔÇô Graph Coloring ÔÇô Satisfiability (SAT) ÔÇó the problem of deciding whether a given Boolean formula is satisfiable 11
- 12. P And NP Summary ÔÇó P = set of problems that can be solved in polynomial time ÔÇô Examples: Fractional Knapsack, ÔǪ ÔÇó NP = set of problems for which a solution can be verified in polynomial time ÔÇô Examples: Fractional Knapsack,ÔǪ, TSP, CNF SAT, 3-CNF SAT ÔÇó Clearly P ´âì NP ÔÇó Open question: Does P = NP? ÔÇô P Ôëá NP
- 13. NP-hard ÔÇó What does NP-hard mean? ÔÇô A lot of times you can solve a problem by reducing it to a different problem. I can reduce Problem B to Problem A if, given a solution to Problem A, I can easily construct a solution to Problem B. (In this case, "easily" means "in polynomial time.ÔÇ£). ÔÇó A problem is NP-hard if all problems in NP are polynomial time reducible to it, ... ÔÇó Every problem in NP is reducible to HC in polynomial time. Ex:- TSP is reducible to HC. 13 Example: lcm(m, n) = m * n / gcd(m, n), B A Ex:- Hamiltonian Cycle
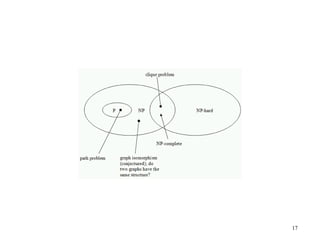
- 14. NP-complete problems ÔÇó A problem is NP-complete if the problem is both ÔÇô NP-hard, and ÔÇô NP.
- 15. Reduction ÔÇó A problem R can be reduced to another problem Q if any instance of R can be rephrased to an instance of Q, the solution to which provides a solution to the instance of R ÔÇô This rephrasing is called a transformation ÔÇó Intuitively: If R reduces in polynomial time to Q, R is ÔÇ£no harder to solveÔÇØ than Q ÔÇó Example: lcm(m, n) = m * n / gcd(m, n), lcm(m,n) problem is reduced to gcd(m, n) problem
- 16. NP-Hard and NP-Complete ÔÇó If R is polynomial-time reducible to Q, we denote this R ´éúp Q ÔÇó Definition of NP-Hard and NP- Complete: ÔÇô If all problems R ´âÄ NP are polynomial-time reducible to Q, then Q is NP-Hard ÔÇô We say Q is NP-Complete if Q is NP-Hard and Q ´âÄ NP ÔÇó If R ´éúp Q and R is NP-Hard, Q is also NP-Hard
- 17. 17
- 18. Summary ÔÇó P is set of problems that can be solved by a deterministic Turing machine in Polynomial time. ÔÇó NP is set of problems that can be solved by a Non-deterministic Turing Machine in Polynomial time. P is subset of NP (any problem that can be solved by deterministic machine in polynomial time can also be solved by non-deterministic machine in polynomial time) but PÔëáNP. 18
- 19. ÔÇó Some problems can be translated into one another in such a way that a fast solution to one problem would automatically give us a fast solution to the other. ÔÇó There are some problems that every single problem in NP can be translated into, and a fast solution to such a problem would automatically give us a fast solution to every problem in NP. This group of problems are known as NP- Complete. Ex:- Clique ÔÇó A problem is NP-hard if an algorithm for solving it can be translated into one for solving any NP- problem (nondeterministic polynomial time) problem. NP-hard therefore means "at least as hard as any NP-problem," although it might, in fact, be harder. 19
- 20. First NP-complete problemÔÇö Circuit Satisfiability (problem definition) ÔÇó Boolean combinational circuit ÔÇô Boolean combinational elements, wired together ÔÇô Each element, inputs and outputs (binary) ÔÇô Limit the number of outputs to 1. ÔÇô Called logic gates: NOT gate, AND gate, OR gate. ÔÇô true table: giving the outputs for each setting of inputs ÔÇô true assignment: a set of boolean inputs. ÔÇô satisfying assignment: a true assignment causing the output to be 1. 20
- 21. Circuit Satisfiability Problem: definition ÔÇó Circuit satisfying problem: given a boolean combinational circuit composed of AND, OR, and NOT, is it stisfiable? ÔÇó CIRCUIT-SAT={<C>: C is a satisfiable boolean circuit} ÔÇó Implication: in the area of computer-aided hardware optimization, if a subcircuit always produces 0, then the subcircuit can be replaced by a simpler subcircuit that omits all gates and just output a 0. 21
- 22. 22 Two instances of circuit satisfiability problems
- 23. Solving circuit-satisfiability problem ÔÇó Intuitive solution: ÔÇô for each possible assignment, check whether it generates 1. ÔÇô suppose the number of inputs is k, then the total possible assignments are 2k. So the running time is ´üù(2k). When the size of the problem is ´üæ(k), then the running time is not polynomial. 23
- 24. 24 Example of reduction of CIRCUIT-SAT to SAT ´üª= x10´âÖ(x10´é½(x7´âÖ x8´âÖ x9)) ´âÖ(x9´é½(x6 ´âÜ x7)) ´âÖ(x8´é½(x5 ´âÜ x6)) ´âÖ(x7´é½(x1´âÖ x2´âÖ x4)) ´âÖ(x6´é½ ´âÿx4)) ´âÖ(x5´é½(x1 ´âÜ x2)) ´âÖ(x4´é½´âÿx3) REDUCTION: ´üª= x10= x7´âÖ x8´âÖ x9=(x1´âÖ x2´âÖ x4) ´âÖ (x5 ´âÜ x6)´âÖ (x6 ´âÜ x7) =(x1´âÖ x2´âÖ x4) ´âÖ ((x1 ´âÜ x2) ´âÜ ´âÿx4)´âÖ (´âÿx4 ´âÜ (x1´âÖ x2´âÖ x4))=ÔǪ.
- 25. Conversion to 3 CNF ÔÇó The result is that in ´üª', each clause has at most three literals. ÔÇó Change each clause into conjunctive normal form as follows: ÔÇô Construct a true table, (small, at most 8 by 4) ÔÇô Write the disjunctive normal form for all true-table items evaluating to 0 ÔÇô Using DeMorgan law to change to CNF. ÔÇó The resulting ´üª'' is in CNF but each clause has 3 or less literals. ÔÇó Change 1 or 2-literal clause into 3-literal clause as follows: ÔÇô If a clause has one literal l, change it to (l´âÜp´âÜq)´âÖ(l´âÜp´âÜ´âÿq)´âÖ (l´âÜ´âÿp´âÜq)´âÖ (l´âÜ´âÿp´âÜ´âÿq). ÔÇô If a clause has two literals (l1´âÜ l2), change it to (l1´âÜ l2 ´âÜp) ´âÖ (l1´âÜ l2 ´âÜ´âÿp). 25
- 26. 26 Example of a polynomial-time reduction: We will reduce the 3CNF-satisfiability problem to the CLIQUE problem
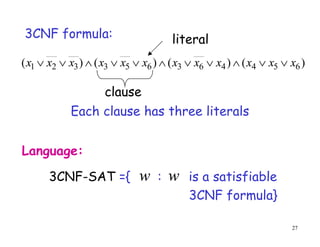
- 27. 27 3CNF formula: ) ( ) ( ) ( ) ( 6 5 4 4 6 3 6 5 3 3 2 1 x x x x x x x x x x x x ´âÜ ´âÜ ´âÖ ´âÜ ´âÜ ´âÖ ´âÜ ´âÜ ´âÖ ´âÜ ´âÜ Each clause has three literals 3CNF-SAT ={ : is a satisfiable 3CNF formula} w w Language: literal clause
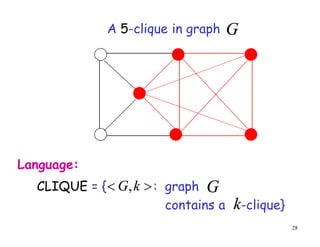
- 28. 28 A 5-clique in graph CLIQUE = { : graph contains a -clique} ´Ç¥ ´Ç╝ k G, G k G Language:
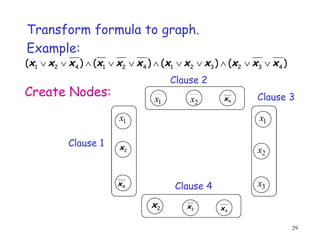
- 29. 29 ) ( ) ( ) ( ) ( 4 3 2 3 2 1 4 2 1 4 2 1 x x x x x x x x x x x x ´âÜ ´âÜ ´âÖ ´âÜ ´âÜ ´âÖ ´âÜ ´âÜ ´âÖ ´âÜ ´âÜ Clause 2 Clause 1 Clause 3 1 x 2 x 1 x 2 x 4 x 1 x 2 x 3 x 2 x 4 x 4 x 3 x Transform formula to graph. Example: Clause 4 Create Nodes:
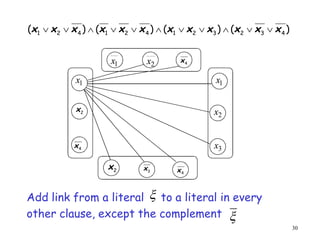
- 30. 30 ) ( ) ( ) ( ) ( 4 3 2 3 2 1 4 2 1 4 2 1 x x x x x x x x x x x x ´âÜ ´âÜ ´âÖ ´âÜ ´âÜ ´âÖ ´âÜ ´âÜ ´âÖ ´âÜ ´âÜ 1 x 2 x 1 x 2 x 4 x 1 x 2 x 2 x 4 x 4 x 3 x 3 x Add link from a literal to a literal in every other clause, except the complement ´ü© ´ü©
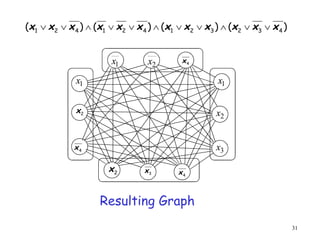
- 31. 31 ) ( ) ( ) ( ) ( 4 3 2 3 2 1 4 2 1 4 2 1 x x x x x x x x x x x x ´âÜ ´âÜ ´âÖ ´âÜ ´âÜ ´âÖ ´âÜ ´âÜ ´âÖ ´âÜ ´âÜ 1 x 2 x 1 x 2 x 4 x 1 x 2 x 3 x 2 x 4 x 4 x 3 x Resulting Graph
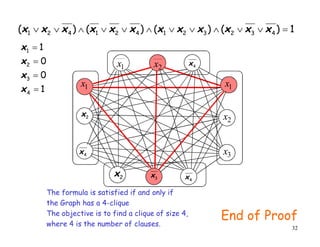
- 32. 32 1 0 0 1 4 3 2 1 ´Ç¢ ´Ç¢ ´Ç¢ ´Ç¢ x x x x 1 ) ( ) ( ) ( ) ( 4 3 2 3 2 1 4 2 1 4 2 1 ´Ç¢ ´âÜ ´âÜ ´âÖ ´âÜ ´âÜ ´âÖ ´âÜ ´âÜ ´âÖ ´âÜ ´âÜ x x x x x x x x x x x x 1 x 2 x 1 x 2 x 4 x 1 x 2 x 3 x 2 x 4 x 4 x 3 x The formula is satisfied if and only if the Graph has a 4-clique The objective is to find a clique of size 4, where 4 is the number of clauses. End of Proof
- 33. 33 Theorem: If: a. Language is NP-complete b. Language is in NP c. is polynomial time reducible to A A B B Then: is NP-complete B
- 34. 34 Corollary: CLIQUE is NP-complete Proof: b. CLIQUE is in NP c. 3CNF-SAT is polynomial reducible to CLIQUE a. 3CNF-SAT is NP-complete Apply previous theorem with A=3CNF-SAT and B=CLIQUE (shown earlier)
- 36. 36 Q. No. 1
- 37. 37 Q. No. 2
- 38. 38 Q. No. 3
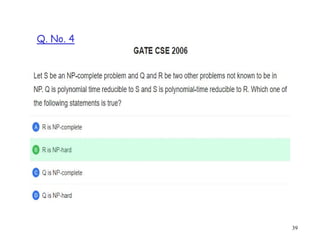
- 39. 39 Q. No. 4
- 40. 40 Q. No. 5
- 41. 41 Q. No. 6
- 42. 42 Q. No. 7
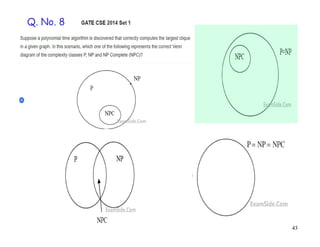
- 43. 43 Q. No. 8
- 44. 44 Explanation: The problem of finding whether there exist a Hamiltonian Cycle or not is NP Hard and NP Complete Both. Finding a Hamiltonian cycle in a graph G = (V,E) with V divisible by 3 is also NP Hard. Q. No. 10 There exist: search problem
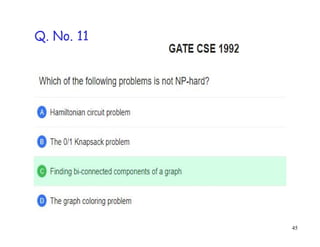
- 45. 45 Q. No. 11
- 46. Thank You 46