Data structure
- 1. RED BLACK TREES Presented By, T. Janani II-M.sc(CS&IT) Nadar Saraswathi College Of Arts & Science, Theni.
- 2. Red - Black Tree A Red-Black tree is a binary search tree where each node is colored either RED or BLACK such that the following invariants are satisfied : 1. The root is BLACK. 2. A RED node can only have BLACK children. 3. Every path from a root down to a Ą°leaf" contains the same number of BLACK nodes. Here a Ą°leafĄ° means a node with less than two children.
- 3. Binary Search Tree : Binary Search Tree (BST) is a good data structure for searching algorithm. It supports 1. Search (key , tree) . 2. Find predecessor(key , tree). 3. Find successor (key , tree). 4. Find minimum (tree). 5. Find maximum(tree). 6. Insertion. 7. Deletion.
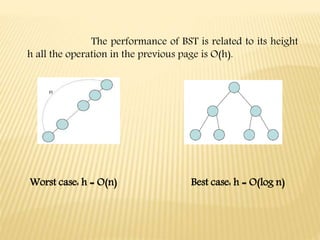
- 4. The performance of BST is related to its height h all the operation in the previous page is O(h). Worst case: h = O(n) Best case: h = O(log n)
- 5. 1. We want a balanced binary search tree. Height of the tree is O(log n). 2. Red-Black Tree is one of the balanced binary search tree.
- 6. Property : 1. Every node is either red or black. 2. The root is black. 3. If a node is red, then both its children are black. 4. For each node, all path from the node to descendant leaves contain the same number of black nodes. ?All path from the node have the same black height
- 7. Insertion 1. When insert a node z, we set the color of z to red 2. This may violate property 2 and 3 3. For property 2, we set the color of root to black after insertion. 4. To fix property 3, we will consider if ? The zĄŊs parent is a left child or right child ? The color of z's uncle y is red or black ? z is a left child or right child 5. We consider the zĄŊs parent is a left child first, the other case can be done by symmetric operation
- 8. There are 4 cases : Case 1 : y is red and z is a left child Case 2 : y is red and z is a right child Case 3 : y is black and z is a left child Case 4 : y is black and z is a right child Case 1 : y is red and z is a left child
- 9. Case 2 : y is a red and z is a right child
- 10. Case 3 : y is a Black and z is a left child
- 11. Case 4 : y is a Black and z is a right child
- 12. Insertion Analysis 1. Case 1 and 2 move z up 2 levels 2. Case 3 and 4 will terminate after some number of steps 3. The height of tree is finite and is O(log n) 4. The running time is O(log n) 5. At most 2 rotations
- 13. Deletion 1. From now on, we always call the deleted node to be z 2. If z is red, it won't violate any property 3. If z is a leaf, it won't violate any property 4. Otherwise z is black and has a child, it will violate property 2, 3, and 4 5. For property 2, set the color of root to black after deletion. To fix property 3 and 4: ? If z's child x (which is the replacing node) is red, set x to black. Done! ? If x is black, add another black to x, so that x will be a doubly black node, and property 3 and 4 are fixed. But property 1 is violated.
- 14. ? To fix property 1, we will consider if ? x is a left child or right child ? The color of x's sibling w is red or black ? The colors of w's children ?We consider x is a left child first, the other case can be done by symmetric operation. There are 4 cases: Case1: w is red Case2: w is black, both w's children are black Case3: w is black, w's left child is red, w's right child is black Case4: w is black, w's right child is red
- 15. Case 1 : W is red
- 16. Case 2 : w is black, both w's children are black
- 17. Case 3 : w is black, w's left child is red, w's right child is black
- 18. Case 4 : w is black, w's right child is red
- 19. Deletion Analysis 1. Case 2 move x up 1 level 2. Case 1, 3 and 4 will terminate after some number of steps. 3. The height of tree is finite and is O(log n) 4. The running time is O(log n) 5. At most 3 rotations
- 20. Conclusion Red-Black Tree is a balanced binary search tree which supports the operation search, find predecessor, find successor, find minimum, find maximum, insertion and deletion in O(log n)-time.
- 21. Thank You