STACK ( LIFO STRUCTURE) - Data Structure
?
3 likes?1,149 views
Stack which is known as LIFO structure.Which is type of the Linear data structure and it is Non-Primitive data structure. Definition:Non primitive data structure are not a basic data structure and depends on other primitive data structure (Integer,float etc). Non primitive data structure can't be operated by machine level instruction directly.
![Algorithm for PUSH Operation
In push operation, we can add elements to the top of the stack, so before push operation, user must check the stack, it should not be a
full.
If stack is already full and when we try to add the elements then error occurs. It is called ¡°Stack Over Flow¡± error.
PUSH(S, TOP, VAL)
This algorithm insert an element X to the top of the stack.
The Stack is represented by vector S which contains N elements.
TOP is a pointer which points to the top element of the Stack.
1.[Check for stack overflow]
If TOP >= N then
Write (¡®Stack Overflow¡¯) Return
2.[Increment TOP]
TOP = TOP + 1
3.[Insert Element]
S [TOP] = VAL
4.[Finished]
Return](https://image.slidesharecdn.com/217beceg004comp-171120075112/85/STACK-LIFO-STRUCTURE-Data-Structure-4-320.jpg)
![Algorithm for POP Operation
In POP operation, we can delete or remove an elements from top of the stack, so before pop operation, user must check the stack, stack
should not be a empty.
If the stack is empty, and we try to pop an element, then error occur. It is called ¡°Stack under Flow¡± error.
POP(S, TOP)
?This algorithm removes an element from the Top of the Stack.
?The Stack is represented by vector S which contains N elements.
?TOP is a pointer which points to the top element of the Stack.
1.[Check for the Underflow on the Stack]
If TOP = 0 then
Write (¡®STACK UNDERFLOW¡¯) Exit
2.[Decrement Pointer]
TOP = TOP - 1
3.[Return former top element of the stack]
Return(S [TOP + 1])](https://image.slidesharecdn.com/217beceg004comp-171120075112/85/STACK-LIFO-STRUCTURE-Data-Structure-5-320.jpg)
![Algorithm of displaying in Stack
DISPLAY(top,i,a[i])
1.If top=0 then
Print ¡®Stack is empty¡¯
Exit
Else
2.For i=top to 0
Print a[i]
End for
3.Exit](https://image.slidesharecdn.com/217beceg004comp-171120075112/85/STACK-LIFO-STRUCTURE-Data-Structure-6-320.jpg)
STACK ( LIFO STRUCTURE) - Data Structure
- 2. Introduction about stack A stack is a linear OR non-primitive list in which insertion and deletion operations are performed at only one end of the list. A stack is Last in First out (LIFO) Structure. A stack is a linear data structure in which elements are added and removed from one end, called top of stack. For example of stack is, consider a stack of plates on the counter in cafeteria. 450 TOP 100 300 230 124 BOTTOM Figure: Stack (vertical representation of stack)
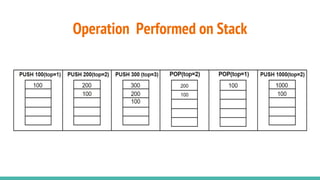
- 3. Operations on stack The insertion operation is referred to as a PUSH operation and deletion operation is referred to as a POP operation. The most accessible element in the stack is known as a TOP element and the least accessible element in the stack is known as a BOTTOM element. Since, the insertion and deletion operation are performed at only one end of the stack. Stack operations are listed below:- (1)Push: The operations that add an element to the top of the stack is called PUSH operation. It is used to insert an element into the stack. (2)Pop: The operation that delete top element from the top of stack is called POP. it is used to delete an element from stack (3)Peep: it is used to retrieve ith element from the top of the stack.
- 4. Algorithm for PUSH Operation In push operation, we can add elements to the top of the stack, so before push operation, user must check the stack, it should not be a full. If stack is already full and when we try to add the elements then error occurs. It is called ¡°Stack Over Flow¡± error. PUSH(S, TOP, VAL) This algorithm insert an element X to the top of the stack. The Stack is represented by vector S which contains N elements. TOP is a pointer which points to the top element of the Stack. 1.[Check for stack overflow] If TOP >= N then Write (¡®Stack Overflow¡¯) Return 2.[Increment TOP] TOP = TOP + 1 3.[Insert Element] S [TOP] = VAL 4.[Finished] Return
- 5. Algorithm for POP Operation In POP operation, we can delete or remove an elements from top of the stack, so before pop operation, user must check the stack, stack should not be a empty. If the stack is empty, and we try to pop an element, then error occur. It is called ¡°Stack under Flow¡± error. POP(S, TOP) ?This algorithm removes an element from the Top of the Stack. ?The Stack is represented by vector S which contains N elements. ?TOP is a pointer which points to the top element of the Stack. 1.[Check for the Underflow on the Stack] If TOP = 0 then Write (¡®STACK UNDERFLOW¡¯) Exit 2.[Decrement Pointer] TOP = TOP - 1 3.[Return former top element of the stack] Return(S [TOP + 1])
- 6. Algorithm of displaying in Stack DISPLAY(top,i,a[i]) 1.If top=0 then Print ¡®Stack is empty¡¯ Exit Else 2.For i=top to 0 Print a[i] End for 3.Exit
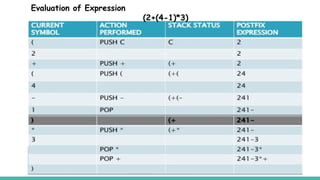
- 7. Operation Performed on Stack
- 8. Application of Stack ¡ñ To reverse a word. You push a given word to stack - letter by letter - and then pop letters from the stack. ¡ñ An "undo" mechanism in text editors; this operation is accomplished by keeping all text changes in a stack. ¡ð Undo/Redo stacks in Excel or Word. ¡ñ Language processing : ¡ð compiler's syntax check for matching braces is implemented by using stack. ¡ñ A stack of plates/books in a cupboard. ¡ñ A garage that is only one car wide. To remove the first car in we have to take out all the other cars in after it. ¡ñ Expression Evolution ¡ñ Expression conversion ¡ñ Function Call
- 10. THANK YOU!!!