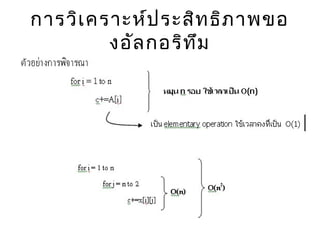
ÓĖüÓĖ▓ÓĖŻÓĖ¦ÓĖ┤Ó╣ĆÓĖäÓĖŻÓĖ▓ÓĖ░ÓĖ½Ó╣īÓĖŁÓĖ▒ÓĖźÓĖüÓĖŁÓĖŻÓĖ┤ÓĖŚÓĖČÓĖĪ(algorithm analysis)
- 2. ŌĆó ÓĖüÓĖ▓ÓĖŻÓĖ¦ÓĖ┤Ó╣ĆÓĖäÓĖŻÓĖ▓ÓĖ░ÓĖ½Ó╣īÓĖŁÓĖ▒ÓĖźÓĖüÓĖŁÓĖŻÓĖ┤ÓĖŚÓĖČÓĖĪ ÓĖĪÓĖĄÓ╣ĆÓĖøÓ╣ēÓĖ▓ÓĖ½ÓĖĪÓĖ▓ÓĖóÓ╣ĆÓĖ×ÓĖĘÓ╣łÓĖŁÓĖ½ÓĖ▓ ÓĖøÓĖŻÓĖ░ÓĖ¬ÓĖ┤ÓĖŚÓĖśÓĖ┤ÓĖĀÓĖ▓ÓĖ×ÓĖéÓĖŁÓĖćÓĖŁÓĖ▒ÓĖźÓĖüÓĖŁÓĖŻÓĖ┤ÓĖŚÓĖČÓĖĪ ÓĖÖÓĖ▒Ó╣łÓĖÖÓĖäÓĖĘÓĖŁÓĖüÓĖ▓ÓĖŻÓĖøÓĖŻÓĖ░ÓĖĪÓĖ▓ÓĖō ÓĖäÓ╣łÓĖ▓ÓĖŚÓĖŻÓĖ▒ÓĖ×ÓĖóÓĖ▓ÓĖüÓĖŻÓĖŚÓĖĄÓ╣łÓĖłÓĖ│ÓĖ▓Ó╣ĆÓĖøÓ╣ćÓĖÖÓĖĢÓ╣ēÓĖŁÓĖćÓ╣āÓĖŖÓ╣ēÓ╣āÓĖÖÓĖüÓĖ▓ÓĖŻÓĖŚÓĖ│ÓĖ▓ÓĖćÓĖ▓ÓĖÖ Ó╣ĆÓĖŖÓ╣łÓĖÖ Ó╣ĆÓĖ¦ÓĖźÓĖ▓ ÓĖ½ÓĖŻÓĖĘÓĖŁ ÓĖ½ÓĖÖÓ╣łÓĖ¦ÓĖóÓĖäÓĖ¦ÓĖ▓ÓĖĪÓĖłÓĖ│ÓĖ▓ ÓĖŁÓĖ▒ÓĖźÓĖüÓĖŁÓĖŻÓĖ┤ÓĖŚÓĖČÓĖĪÓĖ¬Ó╣łÓĖ¦ÓĖÖÓ╣āÓĖ½ÓĖŹÓ╣łÓĖ¢ÓĖ╣ÓĖü ÓĖŁÓĖŁÓĖüÓ╣üÓĖÜÓĖÜÓĖĪÓĖ▓Ó╣ĆÓĖ×ÓĖĘÓ╣łÓĖŁÓ╣āÓĖ½Ó╣ēÓĖ¬ÓĖ▓ÓĖĪÓĖ▓ÓĖŻÓĖ¢ÓĖŻÓĖŁÓĖćÓĖŻÓĖ▒ÓĖÜÓĖłÓĖ│ÓĖ▓ÓĖÖÓĖ¦ÓĖÖÓĖŁÓĖ┤ÓĖÖÓĖ×ÓĖĖÓĖŚ Ó╣äÓĖöÓ╣ēÓ╣äÓĖĪÓ╣łÓĖłÓĖ│ÓĖ▓ÓĖüÓĖ▒ÓĖö ÓĖøÓĖüÓĖĢÓĖ┤Ó╣üÓĖźÓ╣ēÓĖ¦ÓĖøÓĖŻÓĖ░ÓĖ¬ÓĖ┤ÓĖŚÓĖśÓĖ┤ÓĖĀÓĖ▓ÓĖ× ÓĖ½ÓĖŻÓĖĘÓĖŁÓĖäÓĖ¦ÓĖ▓ÓĖĪÓĖŗÓĖ▒ÓĖÜ ÓĖŗÓ╣ēÓĖŁÓĖÖÓĖéÓĖŁÓĖćÓĖŁÓĖ▒ÓĖźÓĖüÓĖŁÓĖŻÓĖ┤ÓĖŚÓĖČÓĖĪÓĖłÓĖ░ÓĖ¦ÓĖ▒ÓĖöÓĖłÓĖ▓ÓĖüÓĖäÓĖ¦ÓĖ▓ÓĖĪÓĖ¬ÓĖ▒ÓĖĪÓĖ×ÓĖ▒ÓĖÖÓĖśÓ╣īÓĖéÓĖŁÓĖć ÓĖłÓĖ│ÓĖ▓ÓĖÖÓĖ¦ÓĖÖÓĖŁÓĖ┤ÓĖÖÓĖ×ÓĖĖÓĖŚÓĖüÓĖ▒ÓĖÜÓ╣ĆÓĖ¦ÓĖźÓĖ▓ÓĖŚÓĖĄÓ╣łÓ╣āÓĖŖÓ╣ēÓ╣āÓĖÖÓĖüÓĖ▓ÓĖŻÓĖŚÓĖ│ÓĖ▓ÓĖćÓĖ▓ÓĖÖ ÓĖ½ÓĖŻÓĖĘÓĖŁ ÓĖ×ÓĖĘÓ╣ēÓĖÖÓĖŚÓĖĄÓ╣łÓĖ½ÓĖÖÓ╣łÓĖ¦ÓĖóÓĖäÓĖ¦ÓĖ▓ÓĖĪÓĖłÓĖ│ÓĖ▓ÓĖŚÓĖĄÓ╣łÓ╣āÓĖŖÓ╣ē (Ó╣āÓĖÖÓĖŻÓĖ░ÓĖóÓĖ░ÓĖ½ÓĖźÓĖ▒ÓĖćÓ╣ĆÓĖŻÓĖĘÓ╣łÓĖŁÓĖćÓĖéÓĖŁÓĖć ÓĖ×ÓĖĘÓ╣ēÓĖÖÓĖŚÓĖĄÓ╣łÓ╣äÓĖĪÓ╣łÓĖ¢ÓĖ╣ÓĖüÓĖ×ÓĖ┤ÓĖłÓĖ▓ÓĖŻÓĖōÓĖ▓ÓĖĪÓĖ▓ÓĖüÓĖÖÓĖ▒ÓĖüÓ╣ĆÓĖÖÓĖĘÓ╣łÓĖŁÓĖćÓĖłÓĖ▓ÓĖüÓĖäÓĖ¦ÓĖ▓ÓĖĪ ÓĖüÓ╣ēÓĖ▓ÓĖ¦ÓĖ½ÓĖÖÓ╣ēÓĖ▓Ó╣āÓĖÖÓĖüÓĖ▓ÓĖŻÓĖ×ÓĖ▒ÓĖÆÓĖÖÓĖ▓ÓĖ½ÓĖÖÓ╣łÓĖ¦ÓĖóÓĖäÓĖ¦ÓĖ▓ÓĖĪÓĖłÓĖ│ÓĖ▓) ŌĆó ÓĖüÓĖ▓ÓĖŻÓĖŁÓĖŁÓĖüÓ╣üÓĖÜÓĖÜÓĖŁÓĖ▒ÓĖźÓĖüÓĖŁÓĖŻÓĖ┤ÓĖŚÓĖČÓĖĪÓ╣ĆÓĖ×ÓĖĘÓ╣łÓĖŁÓ╣üÓĖüÓ╣ēÓĖøÓĖ▒ÓĖŹÓĖ½ÓĖ▓Ó╣āÓĖö Ó╣å
- 3. Asymptotic notationAsymptotic notation Ó╣ĆÓĖäÓĖŻÓĖĘÓ╣łÓĖŁÓĖćÓĖ½ÓĖĪÓĖ▓ÓĖóÓĖŚÓĖĄÓ╣łÓ╣āÓĖŖÓ╣ēÓĖŁÓĖśÓĖ┤ÓĖÜÓĖ▓ÓĖóÓĖüÓĖ▓ÓĖŻÓ╣ĆÓĖĢÓĖ┤ÓĖÜÓ╣éÓĖĢÓĖéÓĖŁÓĖćÓĖ¤ÓĖ▒ÓĖć ÓĖüÓ╣īÓĖŖÓĖ▒Ó╣łÓĖÖ Ó╣éÓĖöÓĖóÓ╣āÓĖÖÓĖüÓĖ▓ÓĖŻÓĖ¦ÓĖ┤Ó╣ĆÓĖäÓĖŻÓĖ▓ÓĖ░ÓĖ½Ó╣īÓĖŁÓĖ▒ÓĖźÓĖüÓĖŁÓĖŻÓĖ┤ÓĖŚÓĖČÓĖĪÓĖłÓĖ░ÓĖÖÓĖ│ÓĖ▓ Ó╣ĆÓĖäÓĖŻÓĖĘÓ╣łÓĖŁÓĖćÓĖ½ÓĖĪÓĖ▓ÓĖóÓĖÖÓĖĄÓ╣ēÓĖĪÓĖ▓Ó╣āÓĖŖÓ╣ēÓ╣āÓĖÖÓĖüÓĖ▓ÓĖŻÓĖŻÓĖ░ÓĖÜÓĖĖ ÓĖøÓĖŻÓĖ░ÓĖ¬ÓĖ┤ÓĖŚÓĖśÓĖ┤ÓĖĀÓĖ▓ÓĖ×ÓĖéÓĖŁÓĖćÓĖŁÓĖ▒ÓĖźÓĖüÓĖŁÓĖŻÓĖ┤ÓĖŚÓĖČÓĖĪ ÓĖĪÓĖĄÓĖ½ÓĖźÓĖ▓ÓĖó ÓĖ¬ÓĖ▒ÓĖŹÓĖźÓĖ▒ÓĖüÓĖ®ÓĖōÓ╣ī ÓĖöÓĖ▒ÓĖćÓĖÖÓĖĄÓ╣ē
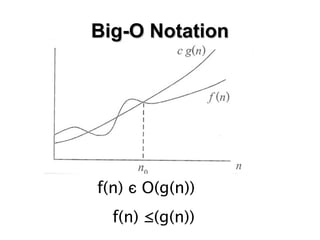
- 4. Big-O NotationBig-O Notation ŌĆó Ó╣ĆÓĖäÓĖŻÓĖĘÓ╣łÓĖŁÓĖćÓĖ½ÓĖĪÓĖ▓ÓĖó ÓĖÜÓĖ┤Ó╣ŖÓĖü-Ó╣éÓĖŁ Ó╣āÓĖŖÓ╣ēÓ╣āÓĖÖÓĖüÓĖ▓ÓĖŻÓĖŻÓĖ░ÓĖÜÓĖĖ ÓĖŚÓĖŻÓĖ▒ÓĖ×ÓĖóÓĖ▓ÓĖüÓĖŻÓĖŚÓĖĄÓ╣łÓ╣āÓĖŖÓ╣ēÓ╣āÓĖÖÓĖüÓĖ▓ÓĖŻÓĖŚÓĖ│ÓĖ▓ÓĖćÓĖ▓ÓĖÖÓĖéÓĖŁÓĖćÓĖŁÓĖ▒ÓĖźÓĖüÓĖŁÓĖŻÓĖ┤ ÓĖŚÓĖČÓĖĪÓ╣ĆÓĖĪÓĖĘÓ╣łÓĖŁÓĖéÓĖÖÓĖ▓ÓĖöÓĖéÓĖŁÓĖćÓĖŁÓĖ┤ÓĖÖÓĖ×ÓĖĖÓĖŚÓ╣ĆÓĖøÓĖźÓĖĄÓ╣łÓĖóÓĖÖÓ╣äÓĖø ŌĆó ÓĖøÓĖüÓĖĢÓĖ┤Ó╣üÓĖźÓ╣ēÓĖ¦ÓĖŚÓĖŻÓĖ▒ÓĖ×ÓĖóÓĖ▓ÓĖüÓĖŻÓĖöÓĖ▒ÓĖćÓĖüÓĖźÓ╣łÓĖ▓ÓĖ¦ÓĖłÓĖ░ÓĖ½ÓĖĪÓĖ▓ÓĖóÓĖ¢ÓĖČÓĖć Ó╣ĆÓĖ¦ÓĖźÓĖ▓ ÓĖÖÓĖ▒Ó╣łÓĖÖÓĖäÓĖĘÓĖŁ ÓĖäÓĖ¦ÓĖ▓ÓĖĪÓĖ¬ÓĖ▒ÓĖĪÓĖ×ÓĖ▒ÓĖÖÓĖśÓ╣īÓĖŻÓĖ░ÓĖ½ÓĖ¦Ó╣łÓĖ▓ÓĖć Ó╣ĆÓĖ¦ÓĖźÓĖ▓ ÓĖüÓĖ▒ÓĖÜ ÓĖéÓĖÖÓĖ▓ÓĖöÓĖéÓĖŁÓĖćÓĖŁÓĖ┤ÓĖÖÓĖ×ÓĖĖÓĖŚ ŌĆó ÓĖŁÓĖ▓ÓĖłÓĖüÓĖźÓ╣łÓĖ▓ÓĖ¦ÓĖćÓ╣łÓĖ▓ÓĖó Ó╣å ÓĖ¦Ó╣łÓĖ▓ ÓĖ½ÓĖ▓ÓĖüÓĖŁÓĖ┤ÓĖÖÓĖ×ÓĖĖÓĖŚÓĖĪÓĖĄÓĖéÓĖÖÓĖ▓ÓĖöÓ╣āÓĖö ÓĖéÓĖÖÓĖ▓ÓĖöÓĖ½ÓĖÖÓĖČÓ╣łÓĖć Ó╣ĆÓĖ¦ÓĖźÓĖ▓ÓĖŚÓĖĄÓ╣łÓ╣āÓĖŖÓ╣ēÓ╣āÓĖÖÓĖüÓĖ▓ÓĖŻÓĖŚÓĖ│ÓĖ▓ÓĖćÓĖ▓ÓĖÖÓĖĪÓĖ▓ÓĖü ÓĖŚÓĖĄÓ╣łÓĖ¬ÓĖĖÓĖö (upper bound) ÓĖłÓĖ░Ó╣ĆÓĖøÓ╣ćÓĖÖÓ╣ĆÓĖŚÓ╣łÓĖ▓Ó╣āÓĖö ÓĖÜÓĖ┤Ó╣ŖÓĖü- Ó╣éÓĖŁ Ó╣ĆÓĖøÓ╣ćÓĖÖÓĖ¤ÓĖ▒ÓĖćÓĖüÓ╣īÓĖŖÓĖ▒Ó╣łÓĖÖÓĖŚÓĖĄÓ╣łÓĖÖÓĖ┤ÓĖóÓĖĪÓ╣āÓĖŖÓ╣ēÓĖĪÓĖ▓ÓĖüÓĖŚÓĖĄÓ╣łÓĖ¬ÓĖĖÓĖöÓ╣āÓĖÖÓĖüÓĖ▓ÓĖŻ
- 5. ŌĆó ÓĖĢÓĖ▒ÓĖ¦ÓĖŁÓĖóÓ╣łÓĖ▓ÓĖć ŌĆó ÓĖäÓĖ¦ÓĖ▓ÓĖĪÓĖ½ÓĖĪÓĖ▓ÓĖóÓĖéÓĖŁÓĖć O(n) ÓĖäÓĖĘÓĖŁ ÓĖ¤ÓĖ▒ÓĖćÓĖüÓ╣īÓĖŖÓĖ▒Ó╣łÓĖÖÓĖÖÓĖ▒Ó╣ēÓĖÖ Ó╣å Ó╣āÓĖŖÓ╣ē Ó╣ĆÓĖ¦ÓĖźÓĖ▓ÓĖŚÓĖ│ÓĖ▓ÓĖćÓĖ▓ÓĖÖÓĖŖÓ╣ēÓĖ▓ÓĖŚÓĖĄÓ╣łÓĖ¬ÓĖĖÓĖö Ōēż n ŌĆó Ó╣ĆÓĖŖÓ╣łÓĖÖ ÓĖŁÓĖ▒ÓĖźÓĖüÓĖŁÓĖŻÓĖ┤ÓĖŚÓĖČÓĖĪ a1 ÓĖĪÓĖĄÓĖøÓĖŻÓĖ░ÓĖ¬ÓĖ┤ÓĖŚÓĖśÓĖ┤ÓĖĀÓĖ▓ÓĖ×Ó╣ĆÓĖøÓ╣ćÓĖÖ O(n2 ) ÓĖ¢Ó╣ēÓĖ▓ n = 10 Ó╣üÓĖźÓ╣ēÓĖ¦ a1 ÓĖłÓĖ░Ó╣āÓĖŖÓ╣ēÓ╣ĆÓĖ¦ÓĖźÓĖ▓ÓĖŚÓĖ│ÓĖ▓ÓĖćÓĖ▓ÓĖÖÓĖŖÓ╣ēÓĖ▓ÓĖŚÓĖĄÓ╣łÓĖ¬ÓĖĖÓĖö 100 ÓĖ½ÓĖÖÓ╣łÓĖ¦ÓĖóÓ╣ĆÓĖ¦ÓĖźÓĖ▓ (ÓĖŻÓĖ▒ÓĖÜÓĖøÓĖŻÓĖ░ÓĖüÓĖ▒ÓĖÖÓĖ¦Ó╣łÓĖ▓Ó╣äÓĖĪÓ╣łÓĖŖÓ╣ēÓĖ▓Ó╣äÓĖøÓĖüÓĖ¦Ó╣łÓĖ▓ÓĖÖÓĖĄÓ╣ē - Ó╣üÓĖĢÓ╣łÓĖŁÓĖ▓ÓĖłÓĖłÓĖ░Ó╣ĆÓĖŻÓ╣ćÓĖ¦ÓĖüÓĖ¦Ó╣łÓĖ▓ÓĖÖÓĖĄÓ╣ēÓ╣äÓĖöÓ╣ē) ŌĆó Ó╣ĆÓĖéÓĖĄÓĖóÓĖÖÓ╣äÓĖöÓ╣ēÓĖ¦Ó╣łÓĖ▓ f(n) čö O(g(n)) Ó╣ĆÓĖ×ÓĖĘÓ╣łÓĖŁÓĖÜÓĖŁÓĖüÓĖ¦Ó╣łÓĖ▓ f(n) Ó╣ĆÓĖøÓ╣ćÓĖÖ ÓĖ¤ÓĖ▒ÓĖćÓĖüÓ╣īÓĖŖÓĖ▒ÓĖÖÓĖŚÓĖĄÓ╣łÓ╣äÓĖĪÓ╣łÓ╣éÓĖĢÓ╣ĆÓĖŻÓ╣ćÓĖ¦ÓĖüÓĖ¦Ó╣łÓĖ▓ g(n) ŌĆó Big-O NotationBig-O Notation
- 6. f(n) čö O(g(n)) f(n) Ōēż(g(n)) Big-O NotationBig-O Notation
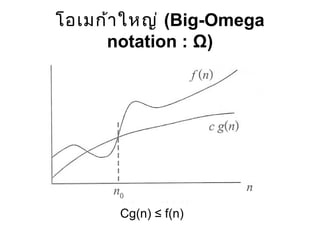
- 8. Ó╣éÓĖŁÓ╣ĆÓĖĪÓĖüÓ╣ēÓĖ▓Ó╣āÓĖ½ÓĖŹÓ╣ł (Big-Omega notation : ╬®) ŌĆó Ó╣éÓĖŁÓ╣ĆÓĖĪÓĖüÓ╣ēÓĖ▓Ó╣āÓĖ½ÓĖŹÓ╣ł ÓĖłÓĖ░Ó╣āÓĖŖÓ╣ēÓĖ¬ÓĖ│ÓĖ▓ÓĖ½ÓĖŻÓĖ▒ÓĖÜÓĖÜÓĖŁÓĖüÓĖ¢ÓĖČÓĖćÓ╣ĆÓĖ¦ÓĖźÓĖ▓ÓĖŚÓĖĄÓ╣łÓ╣āÓĖŖÓ╣ē ÓĖÖÓ╣ēÓĖŁÓĖóÓĖŚÓĖĄÓ╣łÓĖ¬ÓĖĖÓĖö(lower bound) Ó╣ĆÓĖĪÓĖĘÓ╣łÓĖŁÓĖŁÓĖ▒ÓĖźÓĖüÓĖŁÓĖŻÓĖ┤ÓĖŚÓĖČÓĖĪÓĖÖÓĖ▒Ó╣ēÓĖÖ Ó╣å ÓĖŚÓĖ│ÓĖ▓ÓĖćÓĖ▓ÓĖÖÓĖüÓĖ▒ÓĖÜÓĖŁÓĖ┤ÓĖÖÓĖ×ÓĖĖÓĖŚÓĖéÓĖÖÓĖ▓ÓĖöÓ╣āÓĖöÓĖéÓĖÖÓĖ▓ÓĖöÓĖ½ÓĖÖÓĖČÓ╣łÓĖć ŌĆó ÓĖĢÓĖ▒ÓĖ¦ÓĖŁÓĖóÓ╣łÓĖ▓ÓĖć ŌĆó ÓĖäÓĖ¦ÓĖ▓ÓĖĪÓĖ½ÓĖĪÓĖ▓ÓĖóÓĖéÓĖŁÓĖć ╬®(n) ÓĖäÓĖĘÓĖŁ ÓĖ¤ÓĖ▒ÓĖćÓĖüÓ╣īÓĖŖÓĖ▒Ó╣łÓĖÖÓĖÖÓĖ▒Ó╣ēÓĖÖ Ó╣å Ó╣āÓĖŖÓ╣ē Ó╣ĆÓĖ¦ÓĖźÓĖ▓ÓĖŚÓĖ│ÓĖ▓ÓĖćÓĖ▓ÓĖÖÓ╣ĆÓĖŻÓ╣ćÓĖ¦ÓĖŚÓĖĄÓ╣łÓĖ¬ÓĖĖÓĖö Ōēź n ŌĆó Ó╣ĆÓĖŖÓ╣łÓĖÖ ÓĖŁÓĖ▒ÓĖźÓĖüÓĖŁÓĖŻÓĖ┤ÓĖŚÓĖČÓĖĪ a1 ÓĖĪÓĖĄÓĖøÓĖŻÓĖ░ÓĖ¬ÓĖ┤ÓĖŚÓĖśÓĖ┤ÓĖĀÓĖ▓ÓĖ×Ó╣ĆÓĖøÓ╣ćÓĖÖ ╬®(n) ÓĖ¢Ó╣ēÓĖ▓ n = 10 Ó╣üÓĖźÓ╣ēÓĖ¦ a1 ÓĖłÓĖ░Ó╣āÓĖŖÓ╣ēÓ╣ĆÓĖ¦ÓĖźÓĖ▓ÓĖŚÓĖ│ÓĖ▓ÓĖćÓĖ▓ÓĖÖÓ╣ĆÓĖŻÓ╣ćÓĖ¦ ÓĖŚÓĖĄÓ╣łÓĖ¬ÓĖĖÓĖö 10 ÓĖ½ÓĖÖÓ╣łÓĖ¦ÓĖóÓ╣ĆÓĖ¦ÓĖźÓĖ▓ (ÓĖŻÓĖ▒ÓĖÜÓĖøÓĖŻÓĖ░ÓĖüÓĖ▒ÓĖÖÓĖ¦Ó╣łÓĖ▓Ó╣äÓĖĪÓ╣łÓ╣ĆÓĖŻÓ╣ćÓĖ¦Ó╣äÓĖø ÓĖüÓĖ¦Ó╣łÓĖ▓ÓĖÖÓĖĄÓ╣ē - Ó╣üÓĖĢÓ╣łÓĖŁÓĖ▓ÓĖłÓĖłÓĖ░ÓĖŖÓ╣ēÓĖ▓ÓĖüÓĖ¦Ó╣łÓĖ▓ÓĖÖÓĖĄÓ╣ēÓ╣äÓĖöÓ╣ē)
- 9. ŌĆó Ó╣ĆÓĖéÓĖĄÓĖóÓĖÖÓ╣äÓĖöÓ╣ēÓĖ¦Ó╣łÓĖ▓ f(n) čö ╬®(g(n)) Ó╣ĆÓĖ×ÓĖĘÓ╣łÓĖŁÓĖÜÓĖŁÓĖüÓĖ¦Ó╣łÓĖ▓ f(n) Ó╣ĆÓĖøÓ╣ćÓĖÖÓĖ¤ÓĖ▒ÓĖćÓĖüÓ╣īÓĖŖÓĖ▒ÓĖÖÓĖŚÓĖĄÓ╣łÓ╣äÓĖĪÓ╣łÓ╣éÓĖĢÓ╣äÓĖĪÓ╣łÓĖŖÓ╣ēÓĖ▓ÓĖüÓĖ¦Ó╣łÓĖ▓ g(n) ŌĆó Ó╣ĆÓĖŻÓĖ▓ÓĖ¬ÓĖ▓ÓĖĪÓĖ▓ÓĖŻÓĖ¢ÓĖ½ÓĖ▓ÓĖäÓ╣łÓĖ▓ÓĖäÓĖćÓĖĢÓĖ▒ÓĖ¦ÓĖÜÓĖ¦ÓĖü C ÓĖŚÓĖĄÓ╣ł Cg(n) Ōēż f(n) Ó╣éÓĖŁÓ╣ĆÓĖĪÓĖüÓ╣ēÓĖ▓Ó╣āÓĖ½ÓĖŹÓ╣ł (Big-Omega notation : ╬®)
- 10. f(n) čö ╬®(g(n)) Cg(n) Ōēż f(n) Ó╣éÓĖŁÓ╣ĆÓĖĪÓĖüÓ╣ēÓĖ▓Ó╣āÓĖ½ÓĖŹÓ╣ł (Big-Omega notation : ╬®)
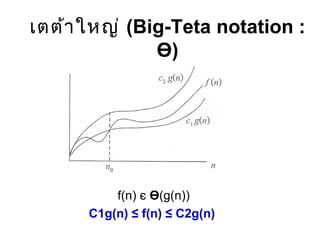
- 11. Ó╣ĆÓĖĢÓĖĢÓ╣ēÓĖ▓Ó╣āÓĖ½ÓĖŹÓ╣ł (Big-Teta notation : ė©) ŌĆó f(n) = ė©(g(n)) ÓĖüÓ╣ćÓĖĢÓ╣łÓĖŁÓ╣ĆÓĖĪÓĖĘÓ╣łÓĖŁ f(n) = O(g(n)) Ó╣üÓĖźÓĖ░ f(n) = ╬®(g(n)) ŌĆó ÓĖÖÓĖ▒Ó╣łÓĖÖÓĖäÓĖĘÓĖŁÓĖéÓĖŁÓĖÜÓĖÜÓĖÖÓ╣üÓĖźÓĖ░ÓĖéÓĖŁÓĖÜÓĖźÓ╣łÓĖ▓ÓĖćÓ╣ĆÓĖøÓ╣ćÓĖÖÓĖ¤ÓĖ▒ÓĖćÓĖüÓ╣īÓĖŖÓĖ▒Ó╣łÓĖÖÓ╣ĆÓĖöÓĖĄÓĖóÓĖ¦ÓĖüÓĖ▒ÓĖÖ
- 12. Ó╣ĆÓĖĢÓĖĢÓ╣ēÓĖ▓Ó╣āÓĖ½ÓĖŹÓ╣ł (Big-Teta notation : ė©) f(n) čö ė©(g(n)) C1g(n) Ōēż f(n) Ōēż C2g(n)
- 13. ÓĖŻÓĖ╣ÓĖø 2.1 ÓĖäÓĖ¦ÓĖ▓ÓĖĪÓĖ¬ÓĖ▒ÓĖĪÓĖ×ÓĖ▒ÓĖÖÓĖśÓ╣īÓĖŻÓĖ░ÓĖ½ÓĖ¦Ó╣łÓĖ▓ÓĖćÓ╣ĆÓĖ¦ÓĖźÓĖ▓ÓĖŚÓĖĄÓ╣łÓ╣āÓĖŖÓ╣ē ÓĖüÓĖ▒ÓĖÜÓĖłÓĖ│ÓĖ▓ÓĖÖÓĖ¦ÓĖÖ ÓĖŁÓĖ┤ÓĖÖÓĖ×ÓĖĖÓĖŚ ÓĖéÓĖŁÓĖćÓĖ¤ÓĖ▒ÓĖćÓĖüÓ╣īÓĖŖÓĖ▒Ó╣łÓĖÖ 10n ÓĖ¤ÓĖ▒ÓĖćÓĖüÓ╣īÓĖŖÓĖ▒Ó╣łÓĖÖ 5n+4 Ó╣üÓĖźÓĖ░ 3n ÓĖ¬ÓĖ▒ÓĖćÓ╣ĆÓĖüÓĖĢÓĖ¦Ó╣łÓĖ▓ ÓĖéÓĖŁÓĖÜÓĖÜÓĖÖ ÓĖüÓĖ▒ÓĖÜ ÓĖéÓĖŁÓĖÜÓĖźÓ╣łÓĖ▓ÓĖć Ó╣ĆÓĖøÓ╣ćÓĖÖÓĖ¤ÓĖ▒ÓĖćÓĖüÓ╣īÓĖŖÓĖ▒Ó╣łÓĖÖÓ╣ĆÓĖöÓĖĄÓĖóÓĖ¦ÓĖüÓĖ▒ÓĖÖ ÓĖ¬ÓĖ▒ÓĖĪÓĖøÓĖŻÓĖ░ÓĖ¬ÓĖ┤ÓĖŚÓĖśÓĖ┤Ó╣īÓĖĢÓ╣łÓĖ▓ÓĖćÓĖüÓĖ▒ÓĖÖ ÓĖäÓĖ¦ÓĖ▓ÓĖĪÓĖ½ÓĖĪÓĖ▓ÓĖóÓĖéÓĖŁÓĖćÓ╣ĆÓĖĢÓĖĢÓ╣ēÓĖ▓ÓĖäÓĖĘÓĖŁ Ó╣āÓĖŖÓ╣ēÓ╣ĆÓĖ¦ÓĖźÓĖ▓ Ó╣ĆÓĖĢÓĖĢÓ╣ēÓĖ▓Ó╣āÓĖ½ÓĖŹÓ╣ł (Big-Teta notation : ė©)
- 14. Ó╣éÓĖŁÓ╣ĆÓĖźÓ╣ćÓĖü (Little-o : o) ŌĆóLittle-o ÓĖäÓĖĘÓĖŁÓĖ¤ÓĖ▒ÓĖćÓĖüÓ╣īÓĖŖÓĖ▒Ó╣łÓĖÖÓĖŚÓĖĄÓ╣łÓ╣äÓĖĪÓ╣łÓ╣üÓĖĢÓĖ░ÓĖéÓĖŁÓĖÜÓĖÜÓĖÖ ÓĖÖÓĖ▒Ó╣łÓĖÖ ÓĖäÓĖĘÓĖŁ ÓĖ¤ÓĖ▒ÓĖćÓĖüÓ╣īÓĖŖÓĖ▒Ó╣łÓĖÖÓĖÖÓĖĄÓ╣ē ÓĖŚÓĖ│ÓĖ▓ÓĖćÓĖ▓ÓĖÖÓĖŖÓ╣ēÓĖ▓ÓĖŚÓĖĄÓ╣łÓĖ¬ÓĖĖÓĖö < n ŌĆóÓĖäÓĖĘÓĖŁ o(g(n)) ÓĖäÓĖĘÓĖŁÓ╣ĆÓĖŗÓĖĢÓĖéÓĖŁÓĖćÓĖ¤ÓĖ▒ÓĖćÓĖüÓ╣īÓĖŖÓĖ▒ÓĖÖÓĖŚÓĖĄÓ╣łÓ╣éÓĖĢ ÓĖŖÓ╣ēÓĖ▓ÓĖüÓĖ¦Ó╣łÓĖ▓ g(n) ŌĆóÓ╣ĆÓĖŖÓ╣łÓĖÖ ÓĖ½ÓĖ▓ÓĖüÓ╣ĆÓĖŻÓĖ▓ÓĖĪÓĖĄ t(n) = n0.98 + 0.05ŌłÜn Ó╣ĆÓĖŻÓĖ▓ÓĖ¬ÓĖ▓ÓĖĪÓĖ▓ÓĖŻÓĖ¢Ó╣ĆÓĖéÓĖĄÓĖóÓĖÖÓ╣äÓĖöÓ╣ēÓ╣ĆÓĖøÓ╣ćÓĖÖ O(n) ÓĖ½ÓĖŻÓĖĘÓĖŁ o(n) ŌĆó Ó╣üÓĖĢÓ╣łÓĖ½ÓĖ▓ÓĖüÓĖŻÓĖ░ÓĖÜÓĖĖÓ╣ĆÓĖøÓ╣ćÓĖÖ Little-o ÓĖłÓĖ░Ó╣ĆÓĖÖÓ╣ēÓĖÖÓ╣āÓĖ½Ó╣ēÓ╣ĆÓĖ½Ó╣ćÓĖÖ ÓĖŖÓĖ▒ÓĖöÓĖ¦Ó╣łÓĖ▓Ó╣äÓĖĪÓ╣łÓĖ¢ÓĖČÓĖć n (Ó╣ĆÓĖ×ÓĖŻÓĖ▓ÓĖ░ÓĖäÓ╣łÓĖ▓ÓĖüÓĖ│ÓĖ▓ÓĖźÓĖ▒ÓĖćÓĖéÓĖŁÓĖć n ÓĖäÓĖĘÓĖŁ
- 15. Ó╣éÓĖŁÓ╣ĆÓĖĪÓĖüÓ╣ēÓĖ▓Ó╣ĆÓĖźÓ╣ćÓĖü (Little-omega : Žē) Little-omega ÓĖäÓĖĘÓĖŁÓĖ¤ÓĖ▒ÓĖćÓĖüÓ╣īÓĖŖÓĖ▒Ó╣łÓĖÖÓĖŚÓĖĄÓ╣łÓ╣äÓĖĪÓ╣łÓ╣üÓĖĢÓĖ░ÓĖéÓĖŁÓĖÜ ÓĖźÓ╣łÓĖ▓ÓĖć ÓĖÖÓĖ▒Ó╣łÓĖÖÓĖäÓĖĘÓĖŁ ÓĖ¤ÓĖ▒ÓĖćÓĖüÓ╣īÓĖŖÓĖ▒Ó╣łÓĖÖÓĖÖÓĖĄÓ╣ēÓĖŚÓĖ│ÓĖ▓ÓĖćÓĖ▓ÓĖÖÓ╣ĆÓĖŻÓ╣ćÓĖ¦ÓĖŚÓĖĄÓ╣łÓĖ¬ÓĖĖÓĖö > n ÓĖäÓĖĘÓĖŁ Žē(g(n)) ÓĖäÓĖĘÓĖŁÓ╣ĆÓĖŗÓĖĢÓĖéÓĖŁÓĖćÓĖ¤ÓĖ▒ÓĖćÓĖüÓ╣īÓĖŖÓĖ▒ÓĖÖÓĖŚÓĖĄÓ╣łÓ╣éÓĖĢ Ó╣ĆÓĖŻÓ╣ćÓĖ¦ÓĖüÓĖ¦Ó╣łÓĖ▓ g(n)
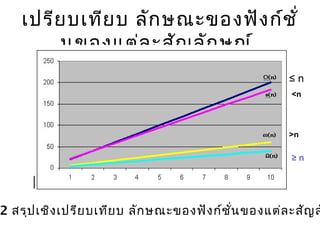
- 16. Ó╣ĆÓĖøÓĖŻÓĖĄÓĖóÓĖÜÓ╣ĆÓĖŚÓĖĄÓĖóÓĖÜ ÓĖźÓĖ▒ÓĖüÓĖ®ÓĖōÓĖ░ÓĖéÓĖŁÓĖćÓĖ¤ÓĖ▒ÓĖćÓĖüÓ╣īÓĖŖÓĖ▒Ó╣ł ÓĖÖÓĖéÓĖŁÓĖćÓ╣üÓĖĢÓ╣łÓĖźÓĖ░ÓĖ¬ÓĖ▒ÓĖŹÓĖźÓĖ▒ÓĖüÓĖ®ÓĖōÓ╣ī 2 ÓĖ¬ÓĖŻÓĖĖÓĖøÓ╣ĆÓĖŖÓĖ┤ÓĖćÓ╣ĆÓĖøÓĖŻÓĖĄÓĖóÓĖÜÓ╣ĆÓĖŚÓĖĄÓĖóÓĖÜ ÓĖźÓĖ▒ÓĖüÓĖ®ÓĖōÓĖ░ÓĖéÓĖŁÓĖćÓĖ¤ÓĖ▒ÓĖćÓĖüÓ╣īÓĖŖÓĖ▒Ó╣łÓĖÖÓĖéÓĖŁÓĖćÓ╣üÓĖĢÓ╣łÓĖźÓĖ░ÓĖ¬ÓĖ▒ÓĖŹÓĖź Ōēż n <n Ōēź n >n
- 17. ÓĖüÓĖ▓ÓĖŻÓĖ½ÓĖ▓Ó╣ĆÓĖŚÓĖŁÓĖĪÓĖŚÓĖĄÓ╣łÓ╣éÓĖĢÓ╣ĆÓĖŻÓ╣ćÓĖ¦ÓĖŚÓĖĄÓ╣łÓĖ¬ÓĖĖÓĖöÓ╣āÓĖÖÓĖ¤ÓĖ▒ÓĖć ÓĖüÓ╣īÓĖŖÓĖ▒Ó╣łÓĖÖ ŌĆó ÓĖäÓĖĘÓĖŁ ÓĖŁÓĖ▒ÓĖĢÓĖŻÓĖ▓ÓĖüÓĖ▓ÓĖŻÓ╣ĆÓĖłÓĖŻÓĖ┤ÓĖŹÓ╣ĆÓĖĢÓĖ┤ÓĖÜÓ╣éÓĖĢÓĖéÓĖŁÓĖć ÓĖ¤ÓĖ▒ÓĖćÓĖüÓ╣īÓĖŖÓĖ▒ÓĖÖ ÓĖŚÓĖĄÓ╣łÓ╣üÓĖŚÓĖÖÓĖøÓĖŻÓĖ░ÓĖ¬ÓĖ┤ÓĖŚÓĖśÓĖ┤ÓĖĀÓĖ▓ÓĖ×ÓĖéÓĖŁÓĖćÓĖŁÓĖ▒ÓĖźÓĖüÓĖŁÓĖŻÓĖ┤ ÓĖŚÓĖČÓĖĪ ŌĆó ÓĖŻÓĖ╣ÓĖøÓ╣üÓĖÜÓĖÜÓĖéÓĖŁÓĖćÓĖ¤ÓĖ▒ÓĖćÓĖüÓ╣īÓĖŖÓĖ▒Ó╣łÓĖÖÓĖŚÓĖĄÓ╣łÓĖĪÓĖ▒ÓĖüÓĖ×ÓĖÜÓĖÜÓ╣łÓĖŁÓĖóÓ╣äÓĖöÓ╣ēÓ╣üÓĖüÓ╣ł ŌĆó exponential ÓĖŁÓĖóÓĖ╣Ó╣łÓ╣āÓĖÖÓĖŻÓĖ╣ÓĖø an ŌĆó polynomial ÓĖŁÓĖóÓĖ╣Ó╣łÓ╣āÓĖÖÓĖŻÓĖ╣ÓĖø na (n ÓĖóÓĖü ÓĖüÓĖ│ÓĖ▓ÓĖźÓĖ▒ÓĖćÓĖäÓ╣łÓĖ▓ÓĖäÓĖćÓĖŚÓĖĄÓ╣ł) Ó╣ĆÓĖŖÓ╣łÓĖÖ n3 ŌĆó Linear ÓĖŁÓĖóÓĖ╣Ó╣łÓ╣āÓĖÖÓĖŻÓĖ╣ÓĖø n ŌĆó logarithmic ÓĖŁÓĖóÓĖ╣Ó╣łÓ╣āÓĖÖÓĖŻÓĖ╣ÓĖø logan ŌĆó ÓĖŚÓĖ▒Ó╣ēÓĖć 4 ÓĖŻÓĖ╣ÓĖøÓ╣üÓĖÜÓĖÜ ÓĖłÓĖ░ÓĖĪÓĖĄÓĖŁÓĖ▒ÓĖĢÓĖŻÓĖ▓ÓĖüÓĖ▓ÓĖŻÓ╣ĆÓĖĢÓĖ┤ÓĖÜÓ╣éÓĖĢÓ╣ĆÓĖŻÓĖĄÓĖóÓĖć ÓĖłÓĖ▓ÓĖüÓĖĪÓĖ▓ÓĖüÓ╣äÓĖøÓĖ½ÓĖ▓ÓĖÖÓ╣ēÓĖŁÓĖó n a
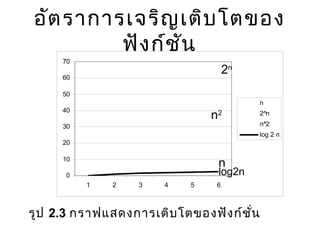
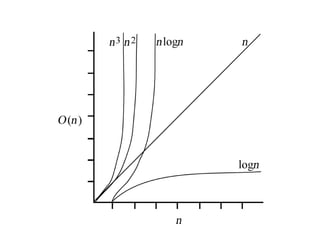
- 18. ÓĖŁÓĖ▒ÓĖĢÓĖŻÓĖ▓ÓĖüÓĖ▓ÓĖŻÓ╣ĆÓĖłÓĖŻÓĖ┤ÓĖŹÓ╣ĆÓĖĢÓĖ┤ÓĖÜÓ╣éÓĖĢÓĖéÓĖŁÓĖć ÓĖ¤ÓĖ▒ÓĖćÓĖüÓ╣īÓĖŖÓĖ▒ÓĖÖ 0 10 20 30 40 50 60 70 1 2 3 4 5 6 n 2^n n^2 log 2 n 2n n2 n log2n ÓĖŻÓĖ╣ÓĖø 2.3 ÓĖüÓĖŻÓĖ▓ÓĖ¤Ó╣üÓĖ¬ÓĖöÓĖćÓĖüÓĖ▓ÓĖŻÓ╣ĆÓĖĢÓĖ┤ÓĖÜÓ╣éÓĖĢÓĖéÓĖŁÓĖćÓĖ¤ÓĖ▒ÓĖćÓĖüÓ╣īÓĖŖÓĖ▒Ó╣łÓĖÖ
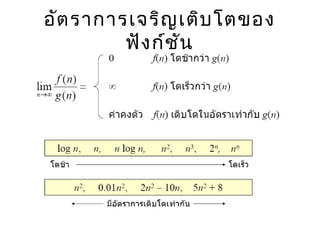
- 21. ÓĖŁÓĖ▒ÓĖĢÓĖŻÓĖ▓ÓĖüÓĖ▓ÓĖŻÓ╣Č─ÓĖĢÓĖ┤ÓĖÜÓ╣éÓĖĢÓŠ║ÓĖŁÓĖćÓĖ¤ÓĖ▒ÓĖćÓĖüÓ╣īÓĖŖÓĖ▒ÓĖÖ ŌĆó ÓĖĢÓĖ▓ÓĖĪÓĖøÓĖŻÓĖ░ÓĖ¬ÓĖ┤ÓĖŚÓĖśÓĖ┤ÓĖĀÓĖ▓ÓĖ×ÓĖéÓĖŁÓĖćÓĖŁÓĖ▒ÓĖźÓĖüÓĖŁÓĖŻÓĖ┤ÓĖśÓĖČÓĖĪÓĖłÓĖ▓ÓĖüÓĖĪÓĖ▓ÓĖüÓĖ¬ÓĖĖÓĖö(ÓĖäÓĖĘÓĖŁÓ╣āÓĖŖÓ╣ē Ó╣ĆÓĖ¦ÓĖźÓĖ▓ÓĖÖÓ╣ēÓĖŁÓĖóÓĖŚÓĖĄÓ╣łÓĖ¬ÓĖĖÓĖö) Ó╣äÓĖøÓĖ½ÓĖ▓ÓĖÖÓ╣ēÓĖŁÓĖóÓĖ¬ÓĖĖÓĖö ŌĆó C > logN > Log2 N > ŌłÜN > N > N log N > N2 > N3 ŌĆ”Nk > 2n , cn > N!
- 22. ÓĖŁÓĖ▒ÓĖĢÓĖŻÓĖ▓ÓĖüÓĖ▓ÓĖŻÓ╣ĆÓĖłÓĖŻÓĖ┤ÓĖŹÓ╣ĆÓĖĢÓĖ┤ÓĖÜÓ╣éÓĖĢÓĖéÓĖŁÓĖć ÓĖ¤ÓĖ▒ÓĖćÓĖüÓ╣īÓĖŖÓĖ▒ÓĖÖ ŌĆóÓĖĢÓĖó1 ŌĆóÓĖłÓĖćÓ╣ĆÓĖŻÓĖĄÓĖóÓĖćÓĖźÓĖ│ÓĖ▓ÓĖöÓĖ▒ÓĖÜÓĖ¤ÓĖ▒ÓĖćÓĖüÓ╣īÓĖŖÓĖ▒ÓĖÖÓĖĢÓ╣łÓĖŁÓ╣äÓĖøÓĖÖÓĖĄÓ╣ēÓĖĢÓĖ▓ÓĖĪ ÓĖŁÓĖ▒ÓĖĢÓĖŻÓĖ▓ÓĖüÓĖ▓ÓĖŻÓ╣ĆÓĖłÓĖŻÓĖ┤ÓĖŹÓ╣ĆÓĖĢÓĖ┤ÓĖÜÓ╣éÓĖĢ ŌĆó0.5n , 1 , log n , n , 10n ŌĆóÓĖłÓĖ░Ó╣äÓĖöÓ╣ēÓĖ¦Ó╣łÓĖ▓ ŌĆó0.5n < 1 < log n < n < 10n
- 23. ŌĆóÓĖĢÓĖó 2 ŌĆóÓĖłÓĖćÓ╣ĆÓĖøÓĖŻÓĖĄÓĖóÓĖÜÓ╣ĆÓĖŚÓĖĄÓĖóÓĖÜÓĖŁÓĖ▒ÓĖĢÓĖŻÓĖ▓ÓĖüÓĖ▓ÓĖŻÓ╣ĆÓĖłÓĖŻÓĖ┤ÓĖŹ Ó╣ĆÓĖĢÓĖ┤ÓĖÜÓ╣éÓĖĢÓĖéÓĖŁÓĖć n10 , 2n ŌĆóÓĖłÓĖ░Ó╣äÓĖöÓ╣ēÓĖ¦Ó╣łÓĖ▓ ŌĆón10 < 2n ÓĖŁÓĖ▒ÓĖĢÓĖŻÓĖ▓ÓĖüÓĖ▓ÓĖŻÓ╣ĆÓĖłÓĖŻÓĖ┤ÓĖŹÓ╣ĆÓĖĢÓĖ┤ÓĖÜÓ╣éÓĖĢÓĖéÓĖŁÓĖć ÓĖ¤ÓĖ▒ÓĖćÓĖüÓ╣īÓĖŖÓĖ▒ÓĖÖ
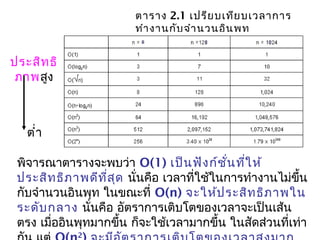
- 24. ÓĖĢÓĖ▓ÓĖŻÓĖ▓ÓĖć 2.1 Ó╣ĆÓĖøÓĖŻÓĖĄÓĖóÓĖÜÓ╣ĆÓĖŚÓĖĄÓĖóÓĖÜÓ╣ĆÓĖ¦ÓĖźÓĖ▓ÓĖüÓĖ▓ÓĖŻ ÓĖŚÓĖ│ÓĖ▓ÓĖćÓĖ▓ÓĖÖÓĖüÓĖ▒ÓĖÜÓĖłÓĖ│ÓĖ▓ÓĖÖÓĖ¦ÓĖÖÓĖŁÓĖ┤ÓĖÖÓĖ×ÓĖĖÓĖŚ ÓĖ×ÓĖ┤ÓĖłÓĖ▓ÓĖŻÓĖōÓĖ▓ÓĖĢÓĖ▓ÓĖŻÓĖ▓ÓĖćÓĖłÓĖ░ÓĖ×ÓĖÜÓĖ¦Ó╣łÓĖ▓ O(1) Ó╣ĆÓĖøÓ╣ćÓĖÖÓĖ¤ÓĖ▒ÓĖćÓĖüÓ╣īÓĖŖÓĖ▒Ó╣łÓĖÖÓĖŚÓĖĄÓ╣łÓ╣āÓĖ½Ó╣ē ÓĖøÓĖŻÓĖ░ÓĖ¬ÓĖ┤ÓĖŚÓĖśÓĖ┤ÓĖĀÓĖ▓ÓĖ×ÓĖöÓĖĄÓĖŚÓĖĄÓ╣łÓĖ¬ÓĖĖÓĖö ÓĖÖÓĖ▒Ó╣łÓĖÖÓĖäÓĖĘÓĖŁ Ó╣ĆÓĖ¦ÓĖźÓĖ▓ÓĖŚÓĖĄÓ╣łÓ╣āÓĖŖÓ╣ēÓ╣āÓĖÖÓĖüÓĖ▓ÓĖŻÓĖŚÓĖ│ÓĖ▓ÓĖćÓĖ▓ÓĖÖÓ╣äÓĖĪÓ╣łÓĖéÓĖČÓ╣ēÓĖÖ ÓĖüÓĖ▒ÓĖÜÓĖłÓĖ│ÓĖ▓ÓĖÖÓĖ¦ÓĖÖÓĖŁÓĖ┤ÓĖÖÓĖ×ÓĖĖÓĖŚ Ó╣āÓĖÖÓĖéÓĖōÓĖ░ÓĖŚÓĖĄÓ╣ł O(n) ÓĖłÓĖ░Ó╣āÓĖ½Ó╣ēÓĖøÓĖŻÓĖ░ÓĖ¬ÓĖ┤ÓĖŚÓĖśÓĖ┤ÓĖĀÓĖ▓ÓĖ×Ó╣āÓĖÖ ÓĖŻÓĖ░ÓĖöÓĖ▒ÓĖÜÓĖüÓĖźÓĖ▓ÓĖć ÓĖÖÓĖ▒Ó╣łÓĖÖÓĖäÓĖĘÓĖŁ ÓĖŁÓĖ▒ÓĖĢÓĖŻÓĖ▓ÓĖüÓĖ▓ÓĖŻÓ╣ĆÓĖĢÓĖ┤ÓĖÜÓ╣éÓĖĢÓĖéÓĖŁÓĖćÓ╣ĆÓĖ¦ÓĖźÓĖ▓ÓĖłÓĖ░Ó╣ĆÓĖøÓ╣ćÓĖÖÓ╣ĆÓĖ¬Ó╣ēÓĖÖ ÓĖĢÓĖŻÓĖć Ó╣ĆÓĖĪÓĖĘÓ╣łÓĖŁÓĖŁÓĖ┤ÓĖÖÓĖ×ÓĖĖÓĖŚÓĖĪÓĖ▓ÓĖüÓĖéÓĖČÓ╣ēÓĖÖ ÓĖüÓ╣ćÓĖłÓĖ░Ó╣āÓĖŖÓ╣ēÓ╣ĆÓĖ¦ÓĖźÓĖ▓ÓĖĪÓĖ▓ÓĖüÓĖéÓĖČÓ╣ēÓĖÖ Ó╣āÓĖÖÓĖ¬ÓĖ▒ÓĖöÓĖ¬Ó╣łÓĖ¦ÓĖÖÓĖŚÓĖĄÓ╣łÓ╣ĆÓĖŚÓ╣łÓĖ▓ 2 ÓĖøÓĖŻÓĖ░ÓĖ¬ÓĖ┤ÓĖŚÓĖśÓĖ┤ ÓĖĀÓĖ▓ÓĖ×ÓĖ¬ÓĖ╣ÓĖć ÓĖĢÓĖ│Ó╣łÓĖ▓
- 25. ÓĖüÓĖ▓ÓĖŻÓĖ¦ÓĖ┤Ó╣ĆÓĖäÓĖŻÓĖ▓ÓĖ░ÓĖ½Ó╣īÓĖøÓĖŻÓĖ░ÓĖ¬ÓĖ┤ÓĖŚÓĖśÓĖ┤ÓĖĀÓĖ▓ÓĖ×ÓĖéÓĖŁ ÓĖćÓĖŁÓĖ▒ÓĖźÓĖüÓĖŁÓĖŻÓĖ┤ÓĖŚÓĖČÓĖĪ ŌĆó Ó╣ĆÓĖŻÓĖ▓ÓĖ¬ÓĖ▓ÓĖĪÓĖ▓ÓĖŻÓĖ¢ÓĖ¦ÓĖ┤Ó╣ĆÓĖäÓĖŻÓĖ▓ÓĖ░ÓĖ½Ó╣īÓĖøÓĖŻÓĖ░ÓĖ¬ÓĖ┤ÓĖŚÓĖśÓĖ┤ÓĖĀÓĖ▓ÓĖ×Ó╣äÓĖöÓ╣ēÓĖłÓĖ▓ÓĖü ÓĖøÓĖŻÓĖ┤ÓĖĪÓĖ▓ÓĖōÓĖäÓĖ│ÓĖ▓ÓĖ¬ÓĖ▒Ó╣łÓĖćÓĖŚÓĖĄÓ╣łÓĖ¢ÓĖ╣ÓĖüÓ╣āÓĖŖÓ╣ēÓĖćÓĖ▓ÓĖÖÓ╣āÓĖÖÓ╣éÓĖøÓĖŻÓ╣üÓĖüÓĖŻÓĖĪ ÓĖŁÓĖ▓ÓĖ©ÓĖ▒ÓĖó Ó╣ĆÓĖäÓĖŻÓĖĘÓ╣łÓĖŁÓĖćÓĖ½ÓĖĪÓĖ▓ÓĖóÓĖŚÓĖĄÓ╣łÓĖüÓĖźÓ╣łÓĖ▓ÓĖ¦ÓĖĪÓĖ▓ÓĖéÓ╣ēÓĖ▓ÓĖćÓĖĢÓ╣ēÓĖÖÓ╣ĆÓĖøÓ╣ćÓĖÖÓĖĢÓĖ▒ÓĖ¦ÓĖüÓĖ│ÓĖ▓ÓĖüÓĖ▒ÓĖÜ Ó╣éÓĖöÓĖó ÓĖüÓĖ▓ÓĖŻÓĖÖÓĖ▒ÓĖÜÓĖäÓĖ│ÓĖ▓ÓĖ¬ÓĖ▒Ó╣łÓĖćÓĖŚÓĖ▒Ó╣ēÓĖćÓĖŚÓĖĄÓ╣łÓ╣ĆÓĖøÓ╣ćÓĖÖÓĖäÓĖ│ÓĖ▓ÓĖ¬ÓĖ▒Ó╣łÓĖćÓĖĪÓĖ╣ÓĖźÓĖÉÓĖ▓ÓĖÖ Ó╣üÓĖźÓĖ░ÓĖäÓĖ│ÓĖ▓ÓĖ¬ÓĖ▒Ó╣łÓĖć ÓĖĪÓĖ▓ÓĖĢÓĖŻÓ╣ĆÓĖ¦ÓĖźÓĖ▓ ÓĖŗÓĖČÓ╣łÓĖćÓĖłÓĖ░ÓĖŚÓĖ│ÓĖ▓Ó╣āÓĖ½Ó╣ēÓ╣äÓĖöÓ╣ēÓĖ¤ÓĖ▒ÓĖćÓĖüÓ╣īÓĖŖÓĖ▒Ó╣łÓĖÖÓĖŚÓĖĄÓ╣łÓĖĪÓĖĄÓĖäÓĖ¦ÓĖ▓ÓĖĪ ÓĖźÓĖ░Ó╣ĆÓĖŁÓĖĄÓĖóÓĖöÓĖ¬ÓĖ╣ÓĖć ÓĖłÓĖ▓ÓĖüÓĖÖÓĖ▒Ó╣ēÓĖÖÓĖłÓĖ░ÓĖäÓ╣łÓĖŁÓĖó Ó╣å ÓĖźÓĖöÓĖäÓĖ¦ÓĖ▓ÓĖĪÓĖŗÓĖ▒ÓĖÜÓĖŗÓ╣ēÓĖŁÓĖÖÓĖźÓĖć Ó╣éÓĖöÓĖóÓĖöÓĖ╣ÓĖłÓĖ▓ÓĖüÓ╣ĆÓĖŚÓĖŁÓĖĪÓĖŚÓĖĄÓ╣łÓ╣āÓĖ½ÓĖŹÓ╣łÓĖŚÓĖĄÓ╣łÓĖ¬ÓĖĖÓĖöÓĖéÓĖŁÓĖćÓĖ¤ÓĖ▒ÓĖćÓĖüÓ╣īÓĖŖÓĖ▒Ó╣łÓĖÖ Ó╣āÓĖÖÓĖüÓĖŻÓĖōÓĖĄÓĖŚÓĖĄÓ╣łÓĖĢÓ╣ēÓĖŁÓĖćÓĖüÓĖ▓ÓĖŻÓĖüÓĖ│ÓĖ▓ÓĖüÓĖ▒ÓĖÜÓĖöÓ╣ēÓĖ¦ÓĖó ÓĖÜÓĖ┤Ó╣ŖÓĖü-Ó╣éÓĖŁ ė©(n2 ) ė©(n log n) Ó╣ĆÓĖ¦ÓĖźÓĖ▓Ó╣āÓĖÖÓĖüÓĖ▓ÓĖŻÓĖŚÓĖ│ÓĖ▓ÓĖćÓĖ▓ÓĖÖÓĖŚÓĖ▒Ó╣ēÓĖćÓĖ½ÓĖĪÓĖöÓĖ¢ÓĖ╣ÓĖü ÓĖüÓĖ│ÓĖ▓ÓĖ½ÓĖÖÓĖöÓ╣éÓĖöÓĖóÓĖ¬Ó╣łÓĖ¦ÓĖÖÓĖŚÓĖĄÓ╣ł 1 Ó╣ĆÓĖ×ÓĖŻÓĖ▓ÓĖ░ÓĖĪÓĖ▒ÓĖÖ Ó╣éÓĖĢÓ╣ĆÓĖŻÓ╣ćÓĖ¦ÓĖüÓĖ¦Ó╣łÓĖ▓
- 27. f(n) = O(n)f(n) = O(n) ÓĖüÓĖ▓ÓĖŻÓĖ¦ÓĖ┤Ó╣ĆÓĖäÓĖŻÓĖ▓ÓĖ░ÓĖ½Ó╣īÓĖøÓĖŻÓĖ░ÓĖ¬ÓĖ┤ÓĖŚÓĖśÓĖ┤ÓĖĀÓĖ▓ÓĖ×ÓĖéÓĖŁ ÓĖćÓĖŁÓĖ▒ÓĖźÓĖüÓĖŁÓĖŻÓĖ┤ÓĖŚÓĖČÓĖĪ ŌĆóÓĖĢÓĖó ŌĆóÓĖŁÓĖ▒ÓĖźÓĖüÓĖŁÓĖŻÓĖ┤ÓĖŚÓĖČÓĖĪ 1 Sum := 0; for I:=1 to n do Sum := Sum+I;
- 28. f(n) = O(1)f(n) = O(1) ŌĆó ÓĖĢÓĖó. ŌĆó ÓĖŁÓĖ▒ÓĖźÓĖüÓĖŁÓĖŻÓĖ┤ÓĖŚÓĖČÓĖĪ 3 Sum := (1+n)*n/2; ÓĖüÓĖ▓ÓĖŻÓĖ¦ÓĖ┤Ó╣ĆÓĖäÓĖŻÓĖ▓ÓĖ░ÓĖ½Ó╣īÓĖøÓĖŻÓĖ░ÓĖ¬ÓĖ┤ÓĖŚÓĖśÓĖ┤ÓĖĀÓĖ▓ÓĖ×ÓĖéÓĖŁ ÓĖćÓĖŁÓĖ▒ÓĖźÓĖüÓĖŁÓĖŻÓĖ┤ÓĖŚÓĖČÓĖĪ
- 30. n4 + n2 + n n4 O(f(n)) =O(f(n)) = ÓĖüÓĖ▓ÓĖŻÓĖ½ÓĖ▓ÓĖäÓ╣łÓĖ▓ Big-Oh ŌĆó ÓĖ½ÓĖ▓Ó╣äÓĖöÓ╣ēÓ╣éÓĖöÓĖóÓĖÖÓĖ│ÓĖ▓ f(n) ÓĖĪÓĖ▓ÓĖüÓĖŻÓĖ░ÓĖŚÓĖ│ÓĖ▓ÓĖöÓĖ▒ÓĖćÓĖÖÓĖĄÓ╣ē 1. ÓĖĢÓĖ▒ÓĖöÓĖ¬ÓĖ▒ÓĖĪÓĖøÓĖŻÓĖ░ÓĖ¬ÓĖ┤ÓĖŚÓĖśÓĖ┤Ó╣īÓĖéÓĖŁÓĖćÓ╣üÓĖĢÓ╣łÓĖźÓĖ░Ó╣ĆÓĖŚÓĖŁÓĖĪÓĖŚÓĖ┤Ó╣ēÓĖć 2. Ó╣ĆÓĖźÓĖĘÓĖŁÓĖüÓ╣ĆÓĖŚÓĖŁÓĖĪÓĖŚÓĖĄÓ╣łÓ╣āÓĖ½ÓĖŹÓ╣łÓĖ¬ÓĖĖÓĖöÓ╣ĆÓĖüÓ╣ćÓĖÜÓ╣äÓĖ¦Ó╣ēÓ╣ĆÓĖøÓ╣ćÓĖÖÓĖäÓĖ│ÓĖ▓ÓĖĢÓĖŁÓĖÜ ŌĆó ÓĖĢÓĖ▒ÓĖ¦ÓĖŁÓĖóÓ╣łÓĖ▓ÓĖćÓ╣ĆÓĖŖÓ╣łÓĖÖ f(n) = 3n4 + 2n2 + n
- 31. Ó╣ĆÓĖĪÓĖĘÓ╣łÓĖŁÓĖ×ÓĖ┤ÓĖłÓĖ▓ÓĖŻÓĖōÓĖ▓ÓĖłÓĖ▓ÓĖü f(n) ÓĖłÓĖ░ÓĖ×ÓĖÜÓĖ¦Ó╣łÓĖ▓ ŌĆó ÓĖŁÓĖ▒ÓĖźÓĖüÓĖŁÓĖŻÓĖ┤ÓĖŚÓĖČÓĖĪ 1 f(n) = n ŌĆó ÓĖŁÓĖ▒ÓĖźÓĖüÓĖŁÓĖŻÓĖ┤ÓĖŚÓĖČÓĖĪ 2 f(n) = n-1 ŌĆó ÓĖŁÓĖ▒ÓĖźÓĖüÓĖŁÓĖŻÓĖ┤ÓĖŚÓĖČÓĖĪ 3 f(n) = 1 ÓĖøÓĖŻÓĖ░ÓĖ¬ÓĖ┤ÓĖŚÓĖśÓĖ┤ÓĖĀÓĖ▓ÓĖ×ÓĖøÓĖŻÓĖ░ÓĖ¬ÓĖ┤ÓĖŚÓĖśÓĖ┤ÓĖĀÓĖ▓ÓĖ×ÓĖĢÓĖ│Ó╣łÓĖ▓ÓĖ¬ÓĖĖÓĖöÓĖĢÓĖ│Ó╣łÓĖ▓ÓĖ¬ÓĖĖÓĖö ÓĖøÓĖŻÓĖ░ÓĖ¬ÓĖ┤ÓĖŚÓĖśÓĖ┤ÓĖĀÓĖ▓ÓĖ×ÓĖøÓĖŻÓĖ░ÓĖ¬ÓĖ┤ÓĖŚÓĖśÓĖ┤ÓĖĀÓĖ▓ÓĖ×ÓĖöÓĖĄÓĖ¬ÓĖĖÓĖöÓĖöÓĖĄÓĖ¬ÓĖĖÓĖö
- 32. ÓĖüÓĖ▓ÓĖŻÓĖ½ÓĖ▓ÓĖäÓ╣łÓĖ▓ Big-Oh ŌĆóÓĖĢÓĖó ÓĖłÓĖćÓĖ½ÓĖ▓ÓĖäÓ╣łÓĖ▓ Big-o ÓĖéÓĖŁÓĖć n3 +2n3 +10 ŌĆó 1. ÓĖĢÓĖ▒ÓĖöÓĖ¬ÓĖ▒ÓĖĪÓĖøÓĖŻÓĖ░ÓĖ¬ÓĖ┤ÓĖŚÓĖśÓĖ┤Ó╣īÓĖéÓĖŁÓĖćÓ╣üÓĖĢÓ╣łÓĖźÓĖ░Ó╣ĆÓĖŚÓĖŁÓĖĪÓĖŚÓĖ┤Ó╣ēÓĖć ÓĖłÓĖ░Ó╣äÓĖöÓ╣ē n3 +n3 ŌĆó 2. Ó╣ĆÓĖźÓĖĘÓĖŁÓĖüÓ╣ĆÓĖŚÓĖŁÓĖĪÓĖŚÓĖĄÓ╣łÓ╣āÓĖ½ÓĖŹÓ╣łÓĖ¬ÓĖĖÓĖöÓ╣ĆÓĖüÓ╣ćÓĖÜÓ╣äÓĖ¦Ó╣ēÓ╣ĆÓĖøÓ╣ćÓĖÖÓĖäÓĖ│ÓĖ▓ÓĖĢÓĖŁÓĖÜ O(f(n)) =O(f(n)) = OO((n3 ))
- 33. ÓĖüÓĖ▓ÓĖŻÓĖ½ÓĖ▓ÓĖäÓ╣łÓĖ▓ Big-Oh ŌĆó ÓĖĢÓĖó ÓĖłÓĖćÓĖ½ÓĖ▓ÓĖäÓ╣łÓĖ▓ Big-o ÓĖéÓĖŁÓĖć 100 ŌĆóF(n) = 100 ŌĆó O(f(n)) =O(f(n)) = O(O(1)1) ŌĆó ÓĖĢÓĖó ÓĖłÓĖćÓĖ½ÓĖ▓ÓĖäÓ╣łÓĖ▓ Big-o ÓĖéÓĖŁÓĖć 100N+1 ŌĆóF(n) = 100N+1 ŌĆó O(f(n)) =O(f(n)) = O(O(N)N)
- 34. ÓĖüÓĖ▓ÓĖŻÓĖ½ÓĖ▓ÓĖäÓ╣łÓĖ▓ Big-Oh ŌĆó ÓĖĢÓĖó ÓĖłÓĖćÓĖ½ÓĖ▓ÓĖäÓ╣łÓĖ▓ Big-o ÓĖéÓĖŁÓĖć 20nlogn+5n = O(nlogn) ŌĆóF(n) = 20nlogn+5n ŌĆóF(n) = nlogn+n ŌĆó O(f(n)) =O(f(n)) = = O(nlogn)
- 35. ŌĆó ÓĖ¬ÓĖĪÓĖĪÓĖĢÓĖ┤Ó╣āÓĖ½Ó╣ēÓ╣üÓĖĢÓ╣łÓĖźÓĖ░Ó╣éÓĖøÓĖŻÓ╣üÓĖüÓĖŻÓĖĪÓ╣āÓĖŖÓ╣ēÓ╣ĆÓĖ¦ÓĖźÓĖ▓Ó╣āÓĖÖÓĖüÓĖ▓ÓĖŻÓĖŚÓĖ│ÓĖ▓ÓĖćÓĖ▓ÓĖÖ Ó╣ĆÓĖøÓ╣ćÓĖÖÓĖöÓĖ▒ÓĖćÓĖÖÓĖĄÓ╣ē ŌĆó prg1 = 3n2 +2n ŌĆó prg2 = 2log2n+6n+n ŌĆó prg3 = n+nlog2n+4n+9 ŌĆó ÓĖłÓĖćÓ╣üÓĖ¬ÓĖöÓĖć Big-O ÓĖéÓĖŁÓĖćÓ╣üÓĖĢÓ╣łÓĖźÓĖ░Ó╣éÓĖøÓĖŻÓ╣üÓĖüÓĖŻÓĖĪÓĖ×ÓĖŻÓ╣ēÓĖŁÓĖĪÓĖŚÓĖ▒Ó╣ēÓĖć Ó╣ĆÓĖŻÓĖĄÓĖóÓĖćÓĖźÓĖ│ÓĖ▓ÓĖöÓĖ▒ÓĖÜÓĖøÓĖŻÓĖ░ÓĖ¬ÓĖ┤ÓĖŚÓĖśÓĖ┤ÓĖĀÓĖ▓ÓĖ×ÓĖéÓĖŁÓĖćÓ╣éÓĖøÓĖŻÓ╣üÓĖüÓĖŻÓĖĪÓĖłÓĖ▓ÓĖüÓĖöÓĖĄÓĖ¬ÓĖĖÓĖö Ó╣äÓĖøÓĖ½ÓĖ▓ÓĖŖÓ╣ēÓĖ▓ÓĖ¬ÓĖĖÓĖö ŌĆó 2Log2n < nlog2n < 3n2 ŌĆó ÓĖłÓĖ░Ó╣äÓĖöÓ╣ē 1. prg2 2. prg3 3.prg1 ÓĖüÓĖ▓ÓĖŻÓĖ¦ÓĖ┤Ó╣ĆÓĖäÓĖŻÓĖ▓ÓĖ░ÓĖ½Ó╣īÓĖøÓĖŻÓĖ░ÓĖ¬ÓĖ┤ÓĖŚÓĖśÓĖ┤ÓĖĀÓĖ▓ÓĖ×ÓĖéÓĖŁ ÓĖćÓĖŁÓĖ▒ÓĖźÓĖüÓĖŁÓĖŻÓĖ┤ÓĖŚÓĖČÓĖĪ
- 36. Ó╣üÓĖÜÓĖÜÓĖØÓĖČÓĖüÓĖ½ÓĖ▒ÓĖö 1. Ó╣āÓĖ½Ó╣ēÓĖźÓĖ│ÓĖ▓ÓĖöÓĖ▒ÓĖÜÓĖŁÓĖ▒ÓĖĢÓĖŻÓĖ▓ÓĖüÓĖ▓ÓĖŻÓ╣ĆÓĖĢÓĖ┤ÓĖÜÓ╣éÓĖĢÓĖéÓĖŁÓĖć ÓĖ¤ÓĖ▒ÓĖćÓĖüÓ╣īÓĖŖÓĖ▒ÓĖÖÓĖłÓĖ▓ÓĖüÓĖÖÓ╣ēÓĖŁÓĖóÓ╣äÓĖøÓĖĪÓĖ▓ÓĖü ŌĆón log n, n3 , 2n , n, n!, log n, 100, n2 2.ÓĖłÓĖćÓĖ½ÓĖ▓ÓĖäÓ╣łÓĖ▓ Big-o ÓĖéÓĖŁÓĖć 12nlogn+0.05n2 3. ÓĖłÓĖćÓĖ½ÓĖ▓ÓĖäÓ╣łÓĖ▓ Big-o ÓĖéÓĖŁÓĖć n1/2 +3nlogn 4. Ó╣āÓĖ½Ó╣ēÓĖźÓĖ│ÓĖ▓ÓĖöÓĖ▒ÓĖÜÓĖŁÓĖ▒ÓĖĢÓĖŻÓĖ▓ÓĖüÓĖ▓ÓĖŻÓ╣Č─ÓĖĢÓĖ┤ÓĖÜÓ╣éÓĖĢÓŠ║ÓĖŁÓĖćÓĖ¤ÓĖ▒ÓĖćÓĖüÓ╣īÓĖŖÓĖ▒ÓĖÖ
- 37. 5. ÓĖłÓĖćÓĖ¦ÓĖ┤Ó╣ĆÓĖäÓĖŻÓĖ▓ÓĖ░ÓĖ½Ó╣īÓĖøÓĖŻÓĖ░ÓĖ¬ÓĖ┤ÓĖŚÓĖśÓĖ┤ÓĖĀÓĖ▓ÓĖ×ÓĖéÓĖŁÓĖćÓĖŁÓĖ▒ÓĖźÓĖüÓĖŁÓĖŻÓĖ┤ÓĖŚÓĖČÓĖĪ ÓĖöÓĖ▒ÓĖćÓĖĢÓ╣łÓĖŁÓ╣äÓĖøÓĖÖÓĖĄÓ╣ē for (j=1; j<n;j++){ sum = sum + j; print sum; } for (i=1; i<n;i++){ for (j=1; j<n;j++){ sum = sum + j; } print sum; }
- 38. 6. ÓĖłÓĖćÓĖ¦ÓĖ┤Ó╣ĆÓĖäÓĖŻÓĖ▓ÓĖ░ÓĖ½Ó╣īÓĖøÓĖŻÓĖ░ÓĖ¬ÓĖ┤ÓĖŚÓĖśÓĖ┤ÓĖĀÓĖ▓ÓĖ×ÓĖéÓĖŁÓĖćÓĖŁÓĖ▒ÓĖźÓĖüÓĖŁÓĖŻÓĖ┤ÓĖŚÓĖČÓĖĪ ÓĖöÓĖ▒ÓĖćÓĖĢÓ╣łÓĖŁÓ╣äÓĖøÓĖÖÓĖĄÓ╣ē For i = 1 To n i = i + 1 Next i For j = 1 To n j = j + 1 Next j