ESSLLI2016 DTS Lecture Day 4-2: More Dependent Types
- 1. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type Introduction to Dependent Type Semantics: More dependent types Daisuke Bekki1,2 Koji Mineshima1,2 1Ochanomizu University / 2CREST, Japan Science and Technology Agency version: August 18, 2016 ESSLLI 2016 course, Bolzano, Italy, August 15-19, 2016. 1 / 41
- 2. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type Disjoint Union Types for Disjunction 2 / 41
- 3. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type Disjoint union type A B is a type for representing disjunctions (A ¡Å B). De?nition ( -Formation/Introduction Rules) A : type B : type A B : type ( F) M : A ¦É1(M) : A B ( I ) N : B ¦É2(N) : A B ( I ) 3 / 41
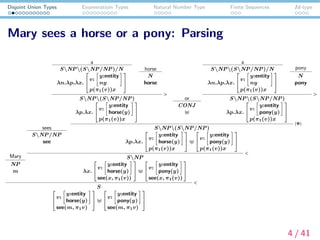
- 4. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type Mary sees a horse or a pony: Parsing Mary NP m sees SNP/NP see a SNP(SNP/NP)/N ¦Ën.¦Ëp.¦Ëx. ? ? v: y:entity ny p(¦Ğ1(v))x ? ? horse N horse SNP(SNP/NP) ¦Ëp.¦Ëx. ? ? v: y:entity horse(y) p(¦Ğ1(v))x ? ? > or CONJ a SNP(SNP/NP)/N ¦Ën.¦Ëp.¦Ëx. ? ? v: y:entity ny p(¦Ğ1(v))x ? ? pony N pony SNP(SNP/NP) ¦Ëp.¦Ëx. ? ? v: y:entity pony(y) p(¦Ğ1(v))x ? ? > SNP(SNP/NP) ¦Ëp.¦Ëx. ? ? v: y:entity horse(y) p(¦Ğ1(v))x ? ? ? ? v: y:entity pony(y) p(¦Ğ1(v))x ? ? ¦µ SNP ¦Ëx. ? ? v: y:entity horse(y) see(x, ¦Ğ1(v)) ? ? ? ? v: y:entity pony(y) see(x, ¦Ğ1(v)) ? ? < S? ? v: y:entity horse(y) see(m, ¦Ğ1v) ? ? ? ? v: y:entity pony(y) see(m, ¦Ğ1v) ? ? < 4 / 41
- 5. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type Disjoint Union Type: the elimination rule -Elimination rule is about how to use L of type A B: De?nition ( -Elimination Rule) L : A B C : (A B) ¡ú type x : A.... M : C(¦É1(x)) i x : B.... N : C(¦É2(x)) i case L of (¦Ëx.M; ¦Ëx.N) : C(L) ( E),i C is a one-place predicate. M is a proof that C(x) holds for any x of type A. N is a proof that C(x) holds for any x of type B. These are enough for proving that C(L) holds for any L of type A B. 5 / 41
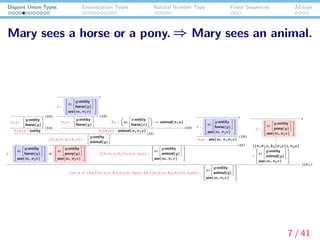
- 6. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type Example: a disjunctive inference Mary sees a horse or a pony. = ? Mary sees an animal. u : ? ? v: y:entity horse(y) see(m, ¦Ğ1v) ? ? ? ? v: y:entity pony(y) see(m, ¦Ğ1v) ? ? ? ? v: y:entity animal(y) see(m, ¦Ğ1v) ? ? true under a signature: k1 : u: x:entity horse(x) ¡ú animal(¦Ğ1u) ¡°Every horse is an animal.¡± k2 : u: x:entity pony(x) ¡ú animal(¦Ğ1u) ¡°Every pony is an animal.¡± 6 / 41
- 7. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type Mary sees a horse or a pony. ? Mary sees an animal. u : ? ? v: y:entity horse(y) see(m, ¦Ğ1v) ? ? ? ? v: y:entity pony(y) see(m, ¦Ğ1v) ? ? ¦Ğ1x : y:entity horse(y) (¦²E) ¦Ğ1¦Ğ1x : entity (¦²E) x : ? ? v: y:entity horse(y) see(m, ¦Ğ1v) ? ? 1 ¦Ğ1x : y:entity horse(y) (¦²E) k1 : u: x:entity horse(x) ¡ú animal(¦Ğ1u) k1(¦Ğ1x) : animal(¦Ğ1¦Ğ1x) (¦²E) (¦Ğ1¦Ğ1x, k1(¦Ğ1x)) : y:entity animal(y) (¦²I ) x : ? ? v: y:entity horse(y) see(m, ¦Ğ1v) ? ? 1 ¦Ğ2x : see(m, ¦Ğ1¦Ğ1x) (¦²E) ((¦Ğ1¦Ğ1x, k1(¦Ğ1x)), ¦Ğ2x) : ? ? v: y:entity animal(y) see(m, ¦Ğ1v) ? ? (¦²I ) x : ? ? v: y:entity pony(y) see(m, ¦Ğ1v) ? ? .... ((¦Ğ1¦Ğ1x, k2(¦Ğ1x)), ¦Ğ2x) : ? ? v: y:entity animal(y) see(m, ¦Ğ1v) ? ? 1 case u of (¦Ëx.((¦Ğ1¦Ğ1x, k1(¦Ğ1x)), ¦Ğ2x); ¦Ëx.((¦Ğ1¦Ğ1x, k2(¦Ğ1x)), ¦Ğ2x)) : ? ? v: y:entity animal(y) see(m, ¦Ğ1v) ? ? ( E),1 7 / 41
- 8. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type Disjunctive antecedents Elbourne (2011): (1) If Mary1 sees [[a horse] or [a pony]]2, she1 waves to it2. Dynamic semantics does not have a straightforward solution for it. A solution via dependent types: Ranta (1994) 8 / 41
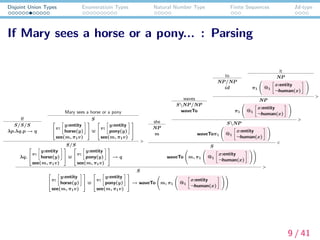
- 9. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type If Mary sees a horse or a pony... : Parsing If S/S/S ¦Ëp.¦Ëq.p ¡ú q Mary sees a horse or a pony S? ? v: y:entity horse(y) see(m, ¦Ğ1v) ? ? ? ? v: y:entity pony(y) see(m, ¦Ğ1v) ? ? S/S ¦Ëq. ? ? v: y:entity horse(y) see(m, ¦Ğ1v) ? ? ? ? v: y:entity pony(y) see(m, ¦Ğ1v) ? ? ¡ú q > she NP m waves SNP/NP waveTo to NP/NP id it NP ¦Ğ1 @1 x:entity ?human(x) NP ¦Ğ1 @1 x:entity ?human(x) > SNP waveTo¦Ğ1 @1 x:entity ?human(x) > S waveTo m, ¦Ğ1 @1 x:entity ?human(x) < S? ? v: y:entity horse(y) see(m, ¦Ğ1v) ? ? ? ? v: y:entity pony(y) see(m, ¦Ğ1v) ? ? ¡ú waveTo m, ¦Ğ1 @1 x:entity ?human(x) > 9 / 41
- 10. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type If Mary sees a horse or a pony... : Type Checking ....? ? v: y:entity horse(y) see(m, ¦Ğ1v) ? ? ? ? v: y:entity pony(y) see(m, ¦Ğ1v) ? ? : type waveTo : entity ¡ú entity ¡ú type (CON ) .... x:entity ?human(x) : type p : ? ? v: y:entity horse(y) see(m, ¦Ğ1v) ? ? ? ? v: y:entity pony(y) see(m, ¦Ğ1v) ? ? .... x:entity ?human(x) 1 @1 x:entity ?human(x) : x:entity ?human(x) (@) ¦Ğ1 @1 x:entity ?human(x) : entity (¦²E) waveTo ¦Ğ1 @1 x:entity ?human(x) : entity ¡ú type (¡úE) m : entity (CON ) waveTo m, ¦Ğ1 @1 x:entity ?human(x) : type (¡úE) ? ?p: ? ? v: y:entity horse(y) see(m, ¦Ğ1v) ? ? ? ? v: y:entity pony(y) see(m, ¦Ğ1v) ? ? ? ? ¡ú waveTo m, ¦Ğ1 @1 x:entity ?human(x) : type (¦°F) 10 / 41
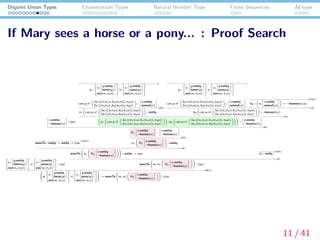
- 11. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type If Mary sees a horse or a pony... : Proof Search ....? ? v: y:entity horse(y) see(m, ¦Ğ1v) ? ? ? ? v: y:entity pony(y) see(m, ¦Ğ1v) ? ? : type waveTo : entity ¡ú entity ¡ú type (CON ) .... x:entity ?human(x) : type p : ? ? v: y:entity horse(y) see(m, ¦Ğ1v) ? ? ? ? v: y:entity pony(y) see(m, ¦Ğ1v) ? ? .... case p of ¦Ëx.((¦Ğ1¦Ğ1x, k1(¦Ğ1x)), ¦Ğ2x); ¦Ëx.((¦Ğ1¦Ğ1x, k2(¦Ğ1x)), ¦Ğ2x) : x:entity animal(x) 1 ¦Ğ1 case p of ¦Ëx.((¦Ğ1¦Ğ1x, k1(¦Ğ1x)), ¦Ğ2x); ¦Ëx.((¦Ğ1¦Ğ1x, k2(¦Ğ1x)), ¦Ğ2x) : entity (¦²E) p : ? ? v: y:entity horse(y) see(m, ¦Ğ1v) ? ? ? ? v: y:entity pony(y) see(m, ¦Ğ1v) ? ? .... case p of ¦Ëx.((¦Ğ1¦Ğ1x, k1(¦Ğ1x)), ¦Ğ2x); ¦Ëx.((¦Ğ1¦Ğ1x, k2(¦Ğ1x)), ¦Ğ2x) : x:entity animal(x) 1 k3 : u: x:entity animal(x) ¡ú ?human(¦Ğ1u) (CON ) k3 case p of ¦Ëx.((¦Ğ1¦Ğ1x, k1(¦Ğ1x)), ¦Ğ2x); ¦Ëx.((¦Ğ1¦Ğ1x, k2(¦Ğ1x)), ¦Ğ2x) : ?human(¦Ğ1) (¡úE) ¦Ğ1 case p of ¦Ëx.((¦Ğ1¦Ğ1x, k1(¦Ğ1x)), ¦Ğ2x); ¦Ëx.((¦Ğ1¦Ğ1x, k2(¦Ğ1x)), ¦Ğ2x) , k3 case p of ¦Ëx.((¦Ğ1¦Ğ1x, k1(¦Ğ1x)), ¦Ğ2x); ¦Ëx.((¦Ğ1¦Ğ1x, k2(¦Ğ1x)), ¦Ğ2x) : x:entity ?human(x) (¡úE) @1 x:entity ?human(x) : x:entity ?human(x) (@) ¦Ğ1 @1 x:entity ?human(x) : entity (¦²E) waveTo ¦Ğ1 @1 x:entity ?human(x) : entity ¡ú type (¡úE) m : entity (CON ) waveTo m, ¦Ğ1 @1 x:entity ?human(x) : type (¡úE) ? ?p: ? ? v: y:entity horse(y) see(m, ¦Ğ1v) ? ? ? ? v: y:entity pony(y) see(m, ¦Ğ1v) ? ? ? ? ¡ú waveTo m, ¦Ğ1 @1 x:entity ?human(x) : type (¦°I ),1 11 / 41
- 12. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type If Mary sees a horse or a pony... : @-Elimination ....? ? v: y:entity horse(y) see(m, ¦Ğ1v) ? ? ? ? v: y:entity pony(y) see(m, ¦Ğ1v) ? ? : type waveTo : entity ¡ú entity ¡ú type (CON ) .... x:entity ?human(x) : type p : ? ? v: y:entity horse(y) see(m, ¦Ğ1v) ? ? ? ? v: y:entity pony(y) see(m, ¦Ğ1v) ? ? .... case p of ¦Ëx.((¦Ğ1¦Ğ1x, k1(¦Ğ1x)), ¦Ğ2x); ¦Ëx.((¦Ğ1¦Ğ1x, k2(¦Ğ1x)), ¦Ğ2x) : x:entity animal(x) 1 ¦Ğ1 case p of ¦Ëx.((¦Ğ1¦Ğ1x, k1(¦Ğ1x)), ¦Ğ2x); ¦Ëx.((¦Ğ1¦Ğ1x, k2(¦Ğ1x)), ¦Ğ2x) : entity (¦²E) p : ? ? v: y:entity horse(y) see(m, ¦Ğ1v) ? ? ? ? v: y:entity pony(y) see(m, ¦Ğ1v) ? ? .... case p of ¦Ëx.((¦Ğ1¦Ğ1x, k1(¦Ğ1x)), ¦Ğ2x); ¦Ëx.((¦Ğ1¦Ğ1x, k2(¦Ğ1x)), ¦Ğ2x) : x:entity animal(x) 1 k3 : u: x:entity animal(x) ¡ú ?human(¦Ğ1u) (CON ) k3 case p of ¦Ëx.((¦Ğ1¦Ğ1x, k1(¦Ğ1x)), ¦Ğ2x); ¦Ëx.((¦Ğ1¦Ğ1x, k2(¦Ğ1x)), ¦Ğ2x) : ?human(¦Ğ1) (¡úE) ¦Ğ1 case p of ¦Ëx.((¦Ğ1¦Ğ1x, k1(¦Ğ1x)), ¦Ğ2x); ¦Ëx.((¦Ğ1¦Ğ1x, k2(¦Ğ1x)), ¦Ğ2x) , k3 case p of ¦Ëx.((¦Ğ1¦Ğ1x, k1(¦Ğ1x)), ¦Ğ2x); ¦Ëx.((¦Ğ1¦Ğ1x, k2(¦Ğ1x)), ¦Ğ2x) : x:entity ?human(x) (¡úE) ¦Ğ1 case p of ¦Ëx.((¦Ğ1¦Ğ1x, k1(¦Ğ1x)), ¦Ğ2x); ¦Ëx.((¦Ğ1¦Ğ1x, k2(¦Ğ1x)), ¦Ğ2x) : entity (¦²E) waveTo ¦Ğ1 case p of ¦Ëx.((¦Ğ1¦Ğ1x, k1(¦Ğ1x)), ¦Ğ2x); ¦Ëx.((¦Ğ1¦Ğ1x, k2(¦Ğ1x)), ¦Ğ2x) : entity ¡ú type (¡úE) m : entity (CON ) waveTo m, ¦Ğ1 case p of ¦Ëx.((¦Ğ1¦Ğ1x, k1(¦Ğ1x)), ¦Ğ2x); ¦Ëx.((¦Ğ1¦Ğ1x, k2(¦Ğ1x)), ¦Ğ2x) : type (¡úE) ? ?p: ? ? v: y:entity horse(y) see(m, ¦Ğ1v) ? ? ? ? v: y:entity pony(y) see(m, ¦Ğ1v) ? ? ? ? ¡ú waveTo m, ¦Ğ1 case p of ¦Ëx.((¦Ğ1¦Ğ1x, k1(¦Ğ1x)), ¦Ğ2x); ¦Ëx.((¦Ğ1¦Ğ1x, k2(¦Ğ1x)), ¦Ğ2x) : type (¦°I ),1 12 / 41
- 13. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type Inaccessibility again (1) If Mary1 sees [[a horse] or [a pony]], she1 waves to it2. (2) * If Mary1 sees [[a horse] or [nothing]], she1 waves to it2. (3) * If Mary1 sees [[nothing] or [a horse]], she1 waves to it2. (4) If Mary1 sees [[a horse] or [nothing]], she1 is unhappy. 13 / 41
- 14. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type Summary: Disjoint union type and disjunction Disjunctive constructions are represented by using disjoint union types. Disjunctive antecedents have been problematic to dynamic semantics, while disjoint union types give it a proper analysis, which implies that anaphora binding is not an issue of variable binding but an issue of proof construction. 14 / 41
- 15. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type Enumeration Type 15 / 41
- 16. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type Rules for enumeration type An enumeration type is a type that is inhabited by a ?nite number of terms. A particular enumeration type is de?ned from a given enumeration of n-number of constructors a1, . . . , an. De?nition ({}-Formation/Introduction Rules) For each i such that 1 ¡Ü i ¡Ü n: {a1, . . . , an} : type ({}F) ai : {a1, . . . , an} ({}I ) 16 / 41
- 17. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type Rules for enumeration type De?nition ({}-Elimination Rule) M : {a1, . . . , an} C : {a1, . . . , an} ¡ú type N1 : C(a1) . . . Nn : C(an) caseM (N1, . . . , Nn) : C(M) ({}E) {}-Elimination rule says how to use M, a proof of an enumeration type. Similar to disjoint union type. C is a one-place predicate. Ni is a proof of C(M) in case M is ai. caseM (N1, . . . , Nn) saids that C holds in every case where M is ai, since we have a proof for each case. 17 / 41
- 18. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type Example I: Bottom Type The ?rst example of enumeration types is the bottom type, the type representing absurdity. Absurdity is understood as a proposition which has no proof, which is straightforwardly represeted as an enumeration type which is inhabited by no term. De?nition (¡Í type) ¡Í def ¡Ô {} De?nition (¡Í-Formation/Elimination Rules) ¡Í : type (¡ÍF) M : ¡Í C : ¡Í ¡ú type caseM () : C(M) (¡ÍE) 18 / 41
- 19. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type EFQ The ¡°Ex Falso Quodlibet¡± (EFQ) rule is straightforwardly derived from ¡Í-Elimination Rule. Thus dependent type theory with enumeration types of arity 0 is stronger than intuitionistic logic. Theorem (Ex Falso Quodlibet) M : ¡Í C : type caseM () : C (EFQ) Proof. M : ¡Í C : type x : ¡Í 1 C : type (WK) ¦Ëx.C : ¡Í ¡ú type (¡úI ),1 caseM () : (¦Ëx.C)M ( ¦Â C) (¡ÍE) 19 / 41
- 20. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type Negation By using ¡Í, the negation of A (notation: ?A) is de?ned as follows: De?nition (?) ?A def ¡Ô A ¡ú ¡Í 20 / 41
- 21. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type Example: Inferences that require EFQ Susan or Mary killed John. Mary didn¡¯t kill John. = ? Susan killed John. u : kill(s, j ) kill(m, j ), v : ?kill(m, j ) kill(s, j ) true u : kill(s, j ) kill(m, j ) x : kill(s, j ) 1 x : kill(m, j ) 1 v : ?kill(m, j ) vx : ¡Í (¡úE) casevx() : kill(s, j ) (EFQ) case u of (¦Ëx.x; ¦Ëx.casevx()) : kill(s, j ) ( E),1 21 / 41
- 22. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type Example II: Top Type The second example of enumeration types is the top type, the type representing necessary truth. Necessary truth is understood as a proposition that there is always a proof (), called an unit. De?nition ( type) def ¡Ô {()} De?nition ( -Formation Rule) : type ( F) () : ( I ) M : C : ¡ú type N : C() caseM (N) : C(M) ( E) 22 / 41
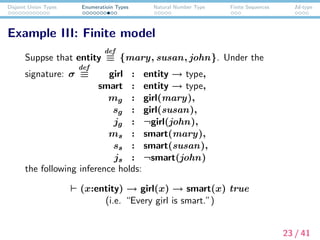
- 23. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type Example III: Finite model Suppse that entity def ¡Ô {mary, susan, john}. Under the signature: ¦Ò def ¡Ô girl : entity ¡ú type, smart : entity ¡ú type, mg : girl(mary), sg : girl(susan), jg : ?girl(john), ms : smart(mary), ss : smart(susan), js : ?smart(john) the following inference holds: (x:entity) ¡ú girl(x) ¡ú smart(x) true (i.e. ¡°Every girl is smart.¡±) 23 / 41
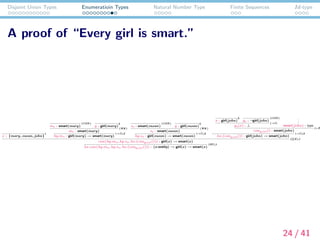
- 24. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type A proof of ¡°Every girl is smart.¡± x : {mary, susan, john} 1 ms : smart(mary) (CON ) y : girl(mary) 2 ms : smart(mary) (WK) ¦Ëy.ms : girl(mary) ¡ú smart(mary) (¡úI ),2 ss : smart(susan) (CON ) y : girl(susan) 2 ss : smart(susan) (WK) ¦Ëy.ss : girl(susan) ¡ú smart(susan) (¡úI ),2 x : girl(john) 3 gs : ?girl(john) (CON ) gs(x) : ¡Í (¡úI ) .... smart(john) : type casegs(x)() : smart(john) (¡ÍE ¦Ëx.(casegs(x)()) : girl(john) ¡ú smart(john) (¡úI ),3 case(¦Ëy.ms, ¦Ëy.ss, ¦Ëx.(casegs(x)())) : girl(x) ¡ú smart(x) ({}E),1 ¦Ëx.case(¦Ëy.ms, ¦Ëy.ss, ¦Ëx.(casegs(x)())) : (x:entity) ¡ú girl(x) ¡ú smart(x) (¦°I ),1 24 / 41
- 25. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type Summary ¡Í and are instances of enumeration types. Generally, ? and ?? propositions can be veri?ed by a single witness, while ? and ?? propositions can be veri?ed only analytically, if they quantify over possibly in?nite domain. In model-theoretic semantics, even ? and ?? propositions can be shown to be true under some ?nite model, while it is not the case in proof-theoretic semantics without enumeration types. entity de?ned in terms of enumeration types behaves as ?nite models, enables us to mimic model-theoretic semantics. 25 / 41
- 26. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type Natural Number Type 26 / 41
- 27. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type Natural Numbers De?nition (N-Formation Rules) N : type (NF) The type N is de?ned by the constructor 0 (zero) and s (the successor function). De?nition (N-Introduction Rules) 0 : N (NI ) n : N s(n) : N (NI ) (NI ) also serves as the introduction rule for s. The digits are de?ned in the following way: 1 def ¡Ô s0, 2 def ¡Ô ss0, 3 def ¡Ô sss0, . . . 27 / 41
- 28. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type Natural Numbers The (NE) rule is the elimination rule of N (and the formulation rule of the natrec constructor). De?nition (N-Elimination Rules) n : N C : N ¡ú type e : C(0) x : N.... i y : C(x) .... i M : C(s(x)) natrec(n, e, ¦Ëx.¦Ëy.M) : C(n) (NE),i Intuitively, the (NE) rule corresponds to the mathematical induction. where e is a proof for 0 and f is a proof for s(n). De?nition (¦Â-reduction rules (one-step)) natrec(0, e, f) ¡ú¦Â e natrec(s(n), e, f) ¡ú¦Â f(n)(natrec(n, e, f)) 28 / 41
- 29. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type Addition and Multiplication The addition operator ¡°+¡± and the multiplication operator ¡°¡¤¡± for nutural numbers illustrate the use of the natrec constructor. De?nition (Addition and Multiplication) m + n def ¡Ô natrec(m, n, ¦Ëx.¦Ëy.s(y)) m ¡¤ n def ¡Ô natrec(m, 0, ¦Ëx.¦Ëy.(y + x)) Exercise: Proove the following theorems: Theorem m : N n : N m + n : N (+F) m : N n : N m ¡¤ n : N (¡¤F) 29 / 41
- 30. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type Example of Addition 2 + 1 ¡Ô s s 0 + s0 ¡ú¦Â natrec(s s 0 , s0, ¦Ëx.¦Ëy.s(y)) ¡ú¦Â (¦Ëx.¦Ëy.s(y))( s 0 )(natrec( s 0 , s0, ¦Ëx.¦Ëy.s(y))) ¦Â s(natrec( s 0 , s0, ¦Ëx.¦Ëy.s(y)) ¡ú¦Â s(¦Ëx.¦Ëy.s(y))( 0 )(natrec( 0 , s0, ¦Ëx.¦Ëy.s(y))) ¡ú¦Â ss(natrec( 0 , s0, ¦Ëx.¦Ëy.s(y))) ¡ú¦Â sss0 ¡Ô 3 m + n def ¡Ô natrec(m, n, ¦Ëx.¦Ëy.s(y)) natrec(0, e, f) ¡ú¦Â e natrec(s( n ), e, f) ¡ú¦Â f( n )(natrec( n , e, f)) 30 / 41
- 31. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type Exercises on natural numbers Prove the following theorems: Theorem 0 + n ¦Â n 0 ¡¤ n ¦Â 0 Theorem 1 + 1 ¦Â 2 Theorem sn =¦Â 1 + n s(m) + n =¦Â s(m + n) s(m) ¡¤ n =¦Â (m ¡¤ n) + n 31 / 41
- 32. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type Finite Sequences 32 / 41
- 33. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type Finite Sequences The disjoint union type, the enumeration types, and the natural number type enable us to de?ne a series of types known as ?nite sequences (Aczel (1980)) De?nition (Finite Sequence) M(n) def ¡Ô natrec(n, ¡Í, ¦Ëx.¦Ëy.(y )) 33 / 41
- 34. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type Finite Sequences Then, M(0), M(1), M(2), . . . are respectively de?ned as types which inhabits 0, 1, 2, . . . canonical terms, as follows. M(0) = natrec(0, ¡Í, ¦Ëx.¦Ëy.(y )) = ¡Í M(s0) = natrec(s0, ¡Í, ¦Ëx.¦Ëy.(y )) = (¦Ëx.¦Ëy.(x ))(0)(natrec(0, ¡Í, ¦Ëx.¦Ëy.(y ))) = ¡Í M(ss0) = natrec(ss0, ¡Í, ¦Ëx.¦Ëy.(y )) = (¦Ëx.¦Ëy.(y ))(s0)(natrec(s0, ¡Í, ¦Ëx.¦Ëy.(y ))) = (¦Ëx.¦Ëy.(y ))(s0)(¡Í ) = (¡Í ) . . . 34 / 41
- 35. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type Finite Sequences M0 is equivalent to ¡Í, thus inhabits no term. M(s0) only inhabits a term ¦É2(). M(ss0) inhabits two terms ¦É1¦É2() and ¦É2(). . . . Exercise Show that: ¦É1¦É2() : M(ss0) ¦É2() : M(ss0) 35 / 41
- 36. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type Intensional Equality type 36 / 41
- 37. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type Extended Syntax A collection of Preterms for an extended theory is augmented with three terms: ¦« =¦« ¦« (intensional types), re?¦«(¦«) (proof terms for the re?exive laws), idpeel(¦«, ¦«) (proof terms for ) De?nition (Preterms) A collection of preterms (notation: ¦«) for an alphabet (Var, Con) is recursively de?ned by the following BNF notation: ¦« := x | c | type | kind | (x:¦«) ¡ú ¦« | ¦Ëx.¦« | ¦«¦« | x:¦« ¦« | (¦«, ¦«) | ¦Ğ1(¦«) | ¦Ğ2(¦«) | ¦« =¦« ¦« | re?¦«(¦«) | idpeel(¦«, ¦«) where x ¡Ê Var and c ¡Ê Con. 37 / 41
- 38. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type Typing Rules De?nition (Id-Formation Rules) A : s M : A N : A M =A N : type (IdF) De?nition (Id-Introduction Rule) A : type M : A re?A(M) : M =A M (IdI ) De?nition (Id-Elimination Rules) E : M1 =A M2 C : (x:A) ¡ú (y:A) ¡ú (x =A y) ¡ú type N : (x:A) ¡ú Cxx(re?A(x)) idpeel(e, N) : CM1M2E (IdE) 38 / 41
- 39. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type Reduction De?nition (Reduction for Id) idpeel(re?A(M), N) ¡ú¦Â N(M) 39 / 41
- 40. Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type Theorems of Id-type Theorem (Symmetry law for Id) A : type M =A N true N =A M true Theorem (Transitivity law for Id) A : type L : A M : A N : A L =A M true M =A N true L =A N true Theorem (Substitution by Id) A : type M : A N : A P : A ¡ú type M =A N true P M true P N true 40 / 41
- 41. References Reference I Aczel, P. H. (1980) ¡°Frege structures and the notions of proposition truth and set¡±, In: J. Barwise, H. J. Keisler, and K. Kunen (eds.): The Kleene Symposium. Amsterdam, North- Holland Publishing Company, pp.31¨C59. Elbourne, P. (2011) Meaning: A Slim Guide to Semantics. Oxford University Press. Ranta, A. (1994) Type-Theoretical Grammar. Oxford University Press. 41 / 41






![Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type
Disjunctive antecedents
Elbourne (2011):
(1) If Mary1 sees [[a horse] or [a pony]]2, she1 waves to it2.
Dynamic semantics does not have a straightforward solution
for it.
A solution via dependent types: Ranta (1994)
8 / 41](https://image.slidesharecdn.com/bekkimineshimaesslli2016-moretypes-200410041828/85/ESSLLI2016-DTS-Lecture-Day-4-2-More-Dependent-Types-8-320.jpg)


![Disjoint Union Types Enumeratioin Types Natural Number Type Finite Sequences Id-type
Inaccessibility again
(1) If Mary1 sees [[a horse] or [a pony]], she1 waves to it2.
(2) * If Mary1 sees [[a horse] or [nothing]], she1 waves to it2.
(3) * If Mary1 sees [[nothing] or [a horse]], she1 waves to it2.
(4) If Mary1 sees [[a horse] or [nothing]], she1 is unhappy.
13 / 41](https://image.slidesharecdn.com/bekkimineshimaesslli2016-moretypes-200410041828/85/ESSLLI2016-DTS-Lecture-Day-4-2-More-Dependent-Types-13-320.jpg)