Differentiation
Download as PPTX, PDF1 like129 views
This document provides the definition and an example of using the quotient rule to differentiate a fraction. The quotient rule is defined as the derivative of the denominator times the numerator minus the numerator times the derivative of the denominator, all over the denominator squared. As an example, the derivative of (3x+4)/(x-4) is calculated using the quotient rule and simplifies to (24x-13)/(x-4)^2.
1 of 4
Download to read offline




Recommended
Factoring



Factoringdaisyrock
?
The document discusses three methods for factoring expressions:
1) Factoring trinomials where a is not equal to 1 using the My Friend Does Math (MFDM) method of multiplying, factoring out, and dividing.
2) Factoring trinomials where a is equal to 1 using the diamond method.
3) Solving two perfect squares by factoring them using the formula (a-b)(a+b) and plugging the results into parentheses.CRMS Calculus 2010 March 30, 2010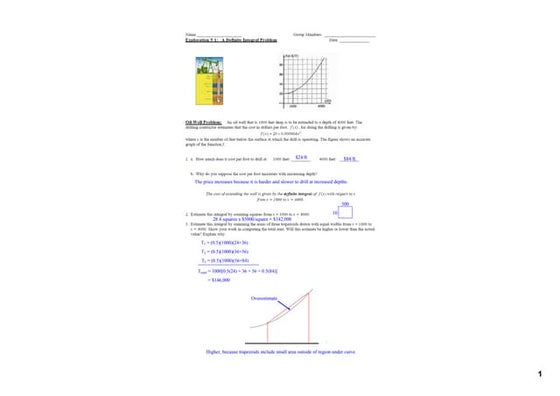



CRMS Calculus 2010 March 30, 2010Fountain Valley School of Colorado
?
The document provides calculations to estimate the total cost of drilling at increasing depths. It calculates the costs from drilling at depths of $24/ft, $36/ft, $56/ft, and $84/ft, finding the total to be $146,000. It then uses trapezoids to estimate the cost, finding a higher estimate because the trapezoids include some area outside the curve. Using smaller trapezoids, it estimates the cost to be $144,500, which is closer to the actual cost.Maxima and minima



Maxima and minimaHarishBabuKaveri
?
This document discusses maxima and minima of functions of two independent variables. It provides the definitions of a relative minimum/maximum point as one where the function value at that point is less than or equal to/greater than or equal to the value at neighboring points. It describes stationary points as those where the function is maximum or minimum, and extreme values as the function values at stationary points. A working rule is given to determine maxima and minima, involving taking partial derivatives and checking signs of second-order derivatives. An example finds the maximum of the function f(x,y)=x^2+y^2+6x+12 at the stationary point (-3,0), with maximum value of 3.Application of derivatives



Application of derivativesParag Parekh & Co. Chartered Accountants
?
The document discusses several topics in calculus including:
1) Finding equations of tangents to curves, points where tangents are parallel to lines, and acceleration when velocity is zero.
2) Rates of change such as how the volume of a balloon is increasing based on the rate its surface area is increasing.
3) Approximating values using concepts like Rolle's theorem, Lagrange's mean value theorem, and determining if functions are increasing or decreasing.
4) Finding maxima and minima of functions by setting the derivative equal to zero and using the second derivative test.
5) Applying calculus to optimization problems to find maximum values.Day 7b examples



Day 7b examplesjchartiersjsd
?
This document discusses limits and how to evaluate them from graphs. It provides examples of limits including lim x^2 as x approaches 2, lim x^2 + 4 as x approaches 2, and lim xcos(2x) as x approaches 0. It also notes that the quotient law cannot be used to evaluate limits if the denominator is undefined. The document assigns problems from pages 137-139 involving limits.11.deflection of beam2



11.deflection of beam2Chhay Teng
?
This document summarizes key concepts related to beam deflection and bending moments:
1. Curvature and bending moment are directly related - as the bending moment increases, so does the curvature of the beam. The elastic curve depicts this relationship graphically.
2. Deflection and rotation angle can be calculated based on the radius of curvature. The rotation angle is equal to the arc length divided by the radius. Deflection is calculated using integrals that relate the slope, rotation angle, and bending moment.
3. The differential equation relating deflection (y), slope (dy/dx), bending moment (M), and flexural rigidity (EI) is: d2y/dx2 = -MMath powerpoint- Polynomial equations and graph of polynomial functions



Math powerpoint- Polynomial equations and graph of polynomial functionsJana Marie Aguilar
?
This document provides information about requirements and concepts for a mathematics course. It defines polynomial expressions and discusses solving polynomial equations by finding their zeros. Properties of polynomial graphs are described, such as being smooth curves without breaks or sharp corners. It also discusses how the multiplicity of a zero affects the graph, whether intercepts cross or touch the x-axis, and if the graph flattens out at higher multiplicities. Examples are given of graphing specific polynomial functions by making tables of values and connecting points with smooth curves.Maxima and minima



Maxima and minimaUmesh Pandey
?
This document discusses maxima and minima in the context of calculus. It provides examples of functions having maximum or minimum values at interior points or endpoints of an interval. It also discusses the first and second derivative tests for identifying maxima and minima. Examples are provided for finding the maximum area of a rectangular field given a perimeter, and finding the maximum volume of a cylinder given a surface area. Finally, some uses of maxima and minima concepts in fields like marketing and manufacturing are outlined.Notes 10-5



Notes 10-5Kate Nowak
?
This document discusses trigonometric equations and functions. It explains that trig equations take the form y = a sin(bx) + c or y = a cos(bx) + c. The parameter c shifts the entire graph up or down, with c > 0 translating up and c < 0 translating down. The line y = c is called the "wrap line". The document also provides an example equation and outlines how to analyze trig formulas by identifying their amplitude, range, frequency, period, and wrap line.Calc 3.9b



Calc 3.9bhartcher
?
This document discusses differentiation rules and differentials. It explains that the differential form of differentiation rules can be used to find differentials of functions. It provides examples of finding differentials of products, composite functions, and using differentials to approximate function values. The key is choosing a value for x that makes calculations easier. Exercises are provided for using differentials to find derivatives of composite functions and to approximate function values.Prim1_secx



Prim1_secxofisico
?
The document derives an integral formula for sec3x in 3 steps. It first shows that the integral of secx dx equals ln|secx + tanx| + C. It then rewrites the integral of sec3x dx in terms of secx and tanx. Finally, it integrates by parts and combines the results with the first step to obtain the formula: ˇŇ sec3x dx = 1/2 ln|secx tanx| + tanx secx + C.Tonethompson



Tonethompsonguest12a053
?
This document provides directions on factoring trinomials by two binomials. It shows the step-by-step process of factoring the trinomial x^2+7x-18 into (x+9)(x-2) through identifying the greatest common factor of the coefficients and then distributing terms to isolate the binomial factors.Algebra 2 Lesson 5-3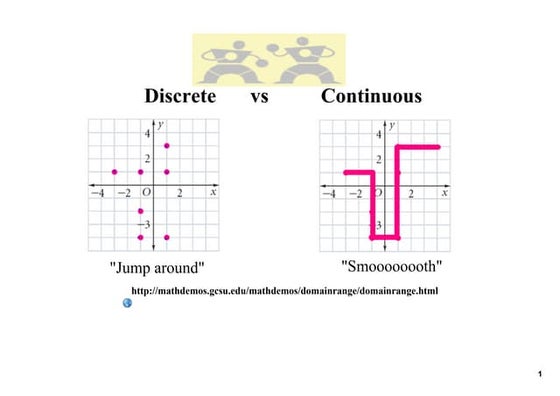



Algebra 2 Lesson 5-3Kate Nowak
?
This document discusses the differences between discrete and continuous domains and ranges for functions. It provides examples of restricted domains and shows how to find the domain and range from graphs. The key points are:
- Continuous functions have a range of values in their domain and range expressed as inequalities.
- To find the domain and range from a graph, identify the lowest and highest x-values for the domain and lowest and highest y-values for the range.
- Examples show restricted domains expressed as sets or inequalities and how to find the corresponding range.Mathcad - modified secant method 2



Mathcad - modified secant method 2?????? ??.
?
This document discusses using the modified secant method to find the root of the function f(x) = ln(2) - 2*ln(x). It provides the initial value of x0 = 3 and time step of ¦Ä = 0.0001. The method is implemented in a ModifiedSecantMethod function, which iteratively calculates new values of x until the difference between iterations is less than 10-10. The result, x_Numerical, converges to approximately 1.4142135624.Ejercicios de la primera clase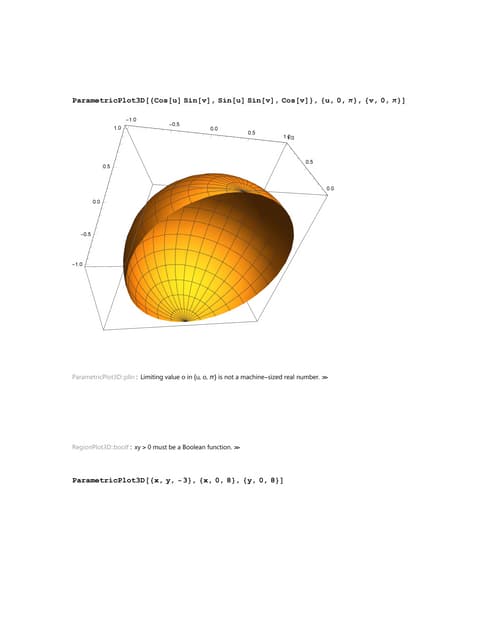



Ejercicios de la primera claseIsrael Garciia
?
The document contains output from several Mathematica functions for 3D plotting and region specification, including ParametricPlot3D, RegionPlot3D, and RegionPlot. Errors are displayed for some functions when limits are invalid or functions are not Boolean. Several examples of valid function calls are also shown generating various 3D surface plots and regions.Lesson 2 math 4 alternative



Lesson 2 math 4 alternativeAlpheZarriz
?
This document discusses place value and the value of whole numbers. It defines digits as single numerical symbols from 0 to 9, and numbers as amounts that can be written with one or more digits. Place value refers to the position of a digit within a number, while value is the amount represented by that digit when multiplied by its place value. Examples are provided to demonstrate how to determine the place and value of digits in various multi-digit numbers written in standard, word, and expanded forms. Key concepts covered include distinguishing digits from numbers, identifying place value and using it to find a digit's value, and representing large numbers readably.Ch14 34



Ch14 34schibu20
?
This document discusses calculating the number of digits needed to write out large numbers. It finds that 11 digits are needed for 43,000,000,000. It also calculates that 95 digits are needed for 999, 369,693,100 digits for 9(9)9, 78 digits for (99)9, and 18 digits for 999. It concludes by showing the relative sizes of these numbers.Maxima and minima



Maxima and minimaGanesh Vadla
?
To find the extreme values (maximum or minimum) of a function f(x,y) of two variables:
1. Take the partial derivatives fx(x,y) and fy(x,y) and set them equal to 0 to find the stationary points.
2. At each stationary point, calculate the second partial derivatives fxx, fyy, and fxy.
3. Use the signs of fxx and the determinant of the Hessian (fxx*fyy - fxy^2) to determine whether the stationary point is a maximum or minimum. If the determinant is positive and fxx is negative, it is a maximum; if the determinant is positive and fxx is positive, itLP Graphical Solution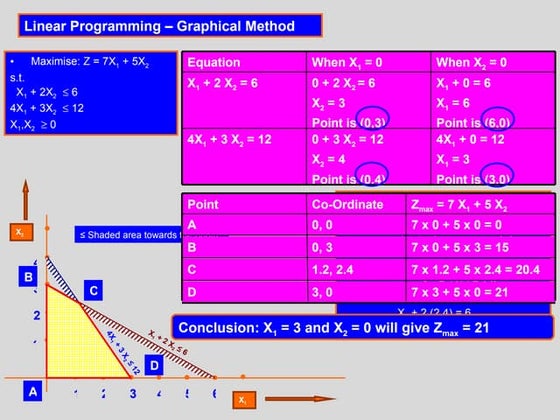



LP Graphical Solutionunemployedmba
?
The document presents a linear programming problem to maximize return from investing Rs. 1,00,000 in two stock portfolios. The maximum investment allowed in each portfolio is Rs. 75,000. Portfolio 1 has a 10% average return and risk rating of 4, while Portfolio 2 has 20% return and risk rating of 9. The objective is to maximize return Z = 0.10X1 + 0.20X2, subject to the constraints that total investment cannot exceed Rs. 1,00,000, individual investments are at most Rs. 75,000 each, risk rating must be below 6, and average return must be at least 12%. The optimal solution is to invest Rs. 60,000 in PortKolmogorov smirnov test



Kolmogorov smirnov testRamesh Giri
?
Kolmogorov-Smirnov test is used to find out the uniformity between the random numbers in a sequece. It can only be used to the pseudo random numbers.Day 2: Basic Properties of Limits



Day 2: Basic Properties of LimitsPablo Antuna
?
In this second day we solve the most basic limits we could find, like the limit of a constant. Then we find the limit of the sum, the product and the quotient of two functions. We solve two simple examples.Lesson 30: Duality In Linear Programming



Lesson 30: Duality In Linear Programmingguest463822
?
Every linear programming problem has a dual problem, which in many cases has an interesting interpretation. The original ("primal") problem and the dual problem have the same extreme value.Antiderivatives



AntiderivativesSilvius
?
The indefinite integral of a function f(x) represents the collection of that function's antiderivatives. The general form of an antiderivative is F(x) + C, where F(x) is any function whose derivative is f(x) and C is an arbitrary constant. Some key properties are that the antiderivative of cf(x) is c times the antiderivative of f(x) and the antiderivative of f(x) ˇŔ g(x) is the antiderivative of f(x) plus/minus the antiderivative of g(x). Tables are also provided listing the antiderivatives of common functions.Math 170 notation



Math 170 notationTyler Murphy
?
some notation commonly seen in calculus 1 courses. Includes the symbol, it's meaning, and sample usage.”µŔí·˝·¨ 2 1-5



”µŔí·˝·¨ 2 1-5Visual Cognition and Modeling Lab
?
This document discusses numerical optimization techniques to find maximum likelihood estimates (MLEs) in 3 steps: 1) Define a log likelihood function, 2) Enter the data, 3) Find the MLE. It also introduces a hierarchy of models, including a general and restricted model. It expresses the likelihoods of each model and maximizes them to select the best model. The likelihood ratio statistic is used to test if the restricted model can be rejected, with the restricted model rejected if the statistic is greater than the chi-squared critical value.02 combinational logic



02 combinational logicZainab Noor
?
This lecture covers digital logic, binary storage, registers, Boolean algebra, and gate-level logic minimization. It introduces binary storage using bits and registers to store multiple bits. Binary logic uses variables that can only have two values (0 or 1) and logic gates that operate on inputs and produce an output. Boolean algebra allows representing logic functions with variables, operations, and standard forms like sum of products. Gate-level logic can be minimized using methods like the map method to reduce the number of gates. Key concepts are binary representation, logic gates, Boolean logic, standard forms, and logic minimization.Entity Framework Interview Questions PDF By ScholarHat



Entity Framework Interview Questions PDF By ScholarHatScholarhat
?
Entity Framework Interview Questions PDF By ScholarHatHelping Autistic Girls Shine Webinar şÝşÝߣs



Helping Autistic Girls Shine Webinar şÝşÝߣsPooky Knightsmith
?
For more information about my speaking and training work, visit: https://www.pookyknightsmith.com/speaking/Meeting the needs of modern students?, Selina McCoy



Meeting the needs of modern students?, Selina McCoyEconomic and Social Research Institute
?
NAPD Annual Symposium
ˇ°Equity in our Schools: Does the system deliver for all young people?ˇ±More Related Content
What's hot (19)
Notes 10-5



Notes 10-5Kate Nowak
?
This document discusses trigonometric equations and functions. It explains that trig equations take the form y = a sin(bx) + c or y = a cos(bx) + c. The parameter c shifts the entire graph up or down, with c > 0 translating up and c < 0 translating down. The line y = c is called the "wrap line". The document also provides an example equation and outlines how to analyze trig formulas by identifying their amplitude, range, frequency, period, and wrap line.Calc 3.9b



Calc 3.9bhartcher
?
This document discusses differentiation rules and differentials. It explains that the differential form of differentiation rules can be used to find differentials of functions. It provides examples of finding differentials of products, composite functions, and using differentials to approximate function values. The key is choosing a value for x that makes calculations easier. Exercises are provided for using differentials to find derivatives of composite functions and to approximate function values.Prim1_secx



Prim1_secxofisico
?
The document derives an integral formula for sec3x in 3 steps. It first shows that the integral of secx dx equals ln|secx + tanx| + C. It then rewrites the integral of sec3x dx in terms of secx and tanx. Finally, it integrates by parts and combines the results with the first step to obtain the formula: ˇŇ sec3x dx = 1/2 ln|secx tanx| + tanx secx + C.Tonethompson



Tonethompsonguest12a053
?
This document provides directions on factoring trinomials by two binomials. It shows the step-by-step process of factoring the trinomial x^2+7x-18 into (x+9)(x-2) through identifying the greatest common factor of the coefficients and then distributing terms to isolate the binomial factors.Algebra 2 Lesson 5-3



Algebra 2 Lesson 5-3Kate Nowak
?
This document discusses the differences between discrete and continuous domains and ranges for functions. It provides examples of restricted domains and shows how to find the domain and range from graphs. The key points are:
- Continuous functions have a range of values in their domain and range expressed as inequalities.
- To find the domain and range from a graph, identify the lowest and highest x-values for the domain and lowest and highest y-values for the range.
- Examples show restricted domains expressed as sets or inequalities and how to find the corresponding range.Mathcad - modified secant method 2



Mathcad - modified secant method 2?????? ??.
?
This document discusses using the modified secant method to find the root of the function f(x) = ln(2) - 2*ln(x). It provides the initial value of x0 = 3 and time step of ¦Ä = 0.0001. The method is implemented in a ModifiedSecantMethod function, which iteratively calculates new values of x until the difference between iterations is less than 10-10. The result, x_Numerical, converges to approximately 1.4142135624.Ejercicios de la primera clase



Ejercicios de la primera claseIsrael Garciia
?
The document contains output from several Mathematica functions for 3D plotting and region specification, including ParametricPlot3D, RegionPlot3D, and RegionPlot. Errors are displayed for some functions when limits are invalid or functions are not Boolean. Several examples of valid function calls are also shown generating various 3D surface plots and regions.Lesson 2 math 4 alternative



Lesson 2 math 4 alternativeAlpheZarriz
?
This document discusses place value and the value of whole numbers. It defines digits as single numerical symbols from 0 to 9, and numbers as amounts that can be written with one or more digits. Place value refers to the position of a digit within a number, while value is the amount represented by that digit when multiplied by its place value. Examples are provided to demonstrate how to determine the place and value of digits in various multi-digit numbers written in standard, word, and expanded forms. Key concepts covered include distinguishing digits from numbers, identifying place value and using it to find a digit's value, and representing large numbers readably.Ch14 34



Ch14 34schibu20
?
This document discusses calculating the number of digits needed to write out large numbers. It finds that 11 digits are needed for 43,000,000,000. It also calculates that 95 digits are needed for 999, 369,693,100 digits for 9(9)9, 78 digits for (99)9, and 18 digits for 999. It concludes by showing the relative sizes of these numbers.Maxima and minima



Maxima and minimaGanesh Vadla
?
To find the extreme values (maximum or minimum) of a function f(x,y) of two variables:
1. Take the partial derivatives fx(x,y) and fy(x,y) and set them equal to 0 to find the stationary points.
2. At each stationary point, calculate the second partial derivatives fxx, fyy, and fxy.
3. Use the signs of fxx and the determinant of the Hessian (fxx*fyy - fxy^2) to determine whether the stationary point is a maximum or minimum. If the determinant is positive and fxx is negative, it is a maximum; if the determinant is positive and fxx is positive, itLP Graphical Solution



LP Graphical Solutionunemployedmba
?
The document presents a linear programming problem to maximize return from investing Rs. 1,00,000 in two stock portfolios. The maximum investment allowed in each portfolio is Rs. 75,000. Portfolio 1 has a 10% average return and risk rating of 4, while Portfolio 2 has 20% return and risk rating of 9. The objective is to maximize return Z = 0.10X1 + 0.20X2, subject to the constraints that total investment cannot exceed Rs. 1,00,000, individual investments are at most Rs. 75,000 each, risk rating must be below 6, and average return must be at least 12%. The optimal solution is to invest Rs. 60,000 in PortKolmogorov smirnov test



Kolmogorov smirnov testRamesh Giri
?
Kolmogorov-Smirnov test is used to find out the uniformity between the random numbers in a sequece. It can only be used to the pseudo random numbers.Day 2: Basic Properties of Limits



Day 2: Basic Properties of LimitsPablo Antuna
?
In this second day we solve the most basic limits we could find, like the limit of a constant. Then we find the limit of the sum, the product and the quotient of two functions. We solve two simple examples.Lesson 30: Duality In Linear Programming



Lesson 30: Duality In Linear Programmingguest463822
?
Every linear programming problem has a dual problem, which in many cases has an interesting interpretation. The original ("primal") problem and the dual problem have the same extreme value.Antiderivatives



AntiderivativesSilvius
?
The indefinite integral of a function f(x) represents the collection of that function's antiderivatives. The general form of an antiderivative is F(x) + C, where F(x) is any function whose derivative is f(x) and C is an arbitrary constant. Some key properties are that the antiderivative of cf(x) is c times the antiderivative of f(x) and the antiderivative of f(x) ˇŔ g(x) is the antiderivative of f(x) plus/minus the antiderivative of g(x). Tables are also provided listing the antiderivatives of common functions.Math 170 notation



Math 170 notationTyler Murphy
?
some notation commonly seen in calculus 1 courses. Includes the symbol, it's meaning, and sample usage.”µŔí·˝·¨ 2 1-5



”µŔí·˝·¨ 2 1-5Visual Cognition and Modeling Lab
?
This document discusses numerical optimization techniques to find maximum likelihood estimates (MLEs) in 3 steps: 1) Define a log likelihood function, 2) Enter the data, 3) Find the MLE. It also introduces a hierarchy of models, including a general and restricted model. It expresses the likelihoods of each model and maximizes them to select the best model. The likelihood ratio statistic is used to test if the restricted model can be rejected, with the restricted model rejected if the statistic is greater than the chi-squared critical value.02 combinational logic



02 combinational logicZainab Noor
?
This lecture covers digital logic, binary storage, registers, Boolean algebra, and gate-level logic minimization. It introduces binary storage using bits and registers to store multiple bits. Binary logic uses variables that can only have two values (0 or 1) and logic gates that operate on inputs and produce an output. Boolean algebra allows representing logic functions with variables, operations, and standard forms like sum of products. Gate-level logic can be minimized using methods like the map method to reduce the number of gates. Key concepts are binary representation, logic gates, Boolean logic, standard forms, and logic minimization.Recently uploaded (20)
Entity Framework Interview Questions PDF By ScholarHat



Entity Framework Interview Questions PDF By ScholarHatScholarhat
?
Entity Framework Interview Questions PDF By ScholarHatHelping Autistic Girls Shine Webinar şÝşÝߣs



Helping Autistic Girls Shine Webinar şÝşÝߣsPooky Knightsmith
?
For more information about my speaking and training work, visit: https://www.pookyknightsmith.com/speaking/Meeting the needs of modern students?, Selina McCoy



Meeting the needs of modern students?, Selina McCoyEconomic and Social Research Institute
?
NAPD Annual Symposium
ˇ°Equity in our Schools: Does the system deliver for all young people?ˇ±Dot NET Core Interview Questions PDF By ScholarHat



Dot NET Core Interview Questions PDF By ScholarHatScholarhat
?
Dot NET Core Interview Questions PDF By ScholarHatHow to Configure Proforma Invoice in Odoo 18 Sales



How to Configure Proforma Invoice in Odoo 18 SalesCeline George
?
In this slide, weˇŻll discuss on how to configure proforma invoice in Odoo 18 Sales module. A proforma invoice is a preliminary invoice that serves as a commercial document issued by a seller to a buyer.B? TEST KI?M TRA GI?A K? 2 - TI?NG ANH 10,11,12 - CHU?N FORM 2025 - GLOBAL SU...



B? TEST KI?M TRA GI?A K? 2 - TI?NG ANH 10,11,12 - CHU?N FORM 2025 - GLOBAL SU...Nguyen Thanh Tu Collection
?
https://app.box.com/s/ij1ty3vm7el9i4qfrr41o756xycbahmgBISNIS BERKAH BERANGKAT KE MEKKAH ISTIKMAL SYARIAH



BISNIS BERKAH BERANGKAT KE MEKKAH ISTIKMAL SYARIAHcoacharyasetiyaki
?
BISNIS BERKAH BERANGKAT KE MEKKAH ISTIKMAL SYARIAHAzure Administrator Interview Questions By ScholarHat



Azure Administrator Interview Questions By ScholarHatScholarhat
?
Azure Administrator Interview Questions By ScholarHatRRB ALP CBT 2 RAC Question Paper MCQ (Railway Assistant Loco Pilot)



RRB ALP CBT 2 RAC Question Paper MCQ (Railway Assistant Loco Pilot)SONU HEETSON
?
RRB ALP CBT 2 RAC Question Paper MCQ PDF Free Download. Railway Assistant Loco Pilot Mechanic Refrigeration and Air Conditioning Important Questions.Intellectual Honesty & Research Integrity.pptx



Intellectual Honesty & Research Integrity.pptxNidhiSharma495177
?
Research Publication & Ethics contains a chapter on Intellectual Honesty and Research Integrity.
Different case studies of intellectual dishonesty and integrity were discussed.Odoo 18 Accounting Access Rights - Odoo 18 şÝşÝߣs



Odoo 18 Accounting Access Rights - Odoo 18 şÝşÝߣsCeline George
?
In this slide, weˇŻll discuss on accounting access rights in odoo 18. To ensure data security and maintain confidentiality, Odoo provides a robust access rights system that allows administrators to control who can access and modify accounting data. ASP.NET Web API Interview Questions By Scholarhat



ASP.NET Web API Interview Questions By ScholarhatScholarhat
?
ASP.NET Web API Interview Questions By ScholarhatRRB ALP CBT 2 Mechanic Motor Vehicle Question Paper (MMV Exam MCQ)



RRB ALP CBT 2 Mechanic Motor Vehicle Question Paper (MMV Exam MCQ)SONU HEETSON
?
RRB ALP CBT 2 Mechanic Motor Vehicle Question Paper. MMV MCQ PDF Free Download for Railway Assistant Loco Pilot Exam.B? TEST KI?M TRA GI?A K? 2 - TI?NG ANH 10,11,12 - CHU?N FORM 2025 - GLOBAL SU...



B? TEST KI?M TRA GI?A K? 2 - TI?NG ANH 10,11,12 - CHU?N FORM 2025 - GLOBAL SU...Nguyen Thanh Tu Collection
?
Differentiation
- 2. QUOTIENT RULE DEFINITION: The quotient rule is defined as the quantity of the denominator times the derivative of the numerator minus the numerator times the derivative of the denominator all over the denominator squared. ? ? ? ? ? ? ? ? ? ? ? ? ? ?? ? .2 xg xfxgxgxf xg xf dx d ??? ?? ? ? ? ? ?
- 3. EXAMPLE SOLUTION Differentiate. Let and . Then, using the quotient rule x xx 34 24 ?? ? ? 34 24 ??? xxxf ? ? xxg ? ? ? ? ? ? ? 2 2424 24 3434 34 x x dx d xxxx dx d x x xx dx d ??????? ?? ? ? ? ? ? ?? ? ? ? ? 2 243 13484 x xxxxx ?????? ? 2 24 343 x xx ?? ? Now simplify.
- 4. Thank you







