Distribusi normal
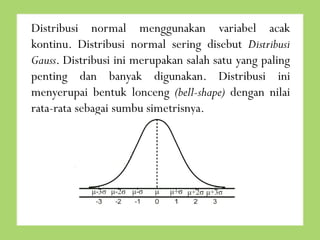
- 2. Distribusi normal menggunakan variabel acak kontinu. Distribusi normal sering disebut Distribusi Gauss. Distribusi ini merupakan salah satu yang paling penting dan banyak digunakan. Distribusi ini menyerupai bentuk lonceng (bell-shape) dengan nilai rata-rata sebagai sumbu simetrisnya.
- 3. Variabel acak kontinu X mempunyai fungsi densitas pada X = x dengan persamaan: 1 x 2 ( ) 1 2 f ( x) e 2 dengan : nilai konstan yang ditulis hingga 4 desimal 3,1416 e = bilangan konstan yang ditulis hingga 4 desimal, e =2,7183 parameter, merupakan rata-rata untuk distribusi parameter, merupakan simpangan baku untuk distribusi Jika nilai x mempunyai batas < x < , maka dikatakan bahwa variabel acak X berdistribusi normal.
- 4. Sifat-sifat penting dari distribusi normal, yaitu: 1. Grafiknya selalu ada di atas sumbu-X (horizontal) 2. Bentuk simetrik terhadap x = 袖 3. Mempunyai modus pada x = 袖 sebesar 0,3989/ 4. Grafik mendekati (berasimtutkan) sumbu-X pada X = 袖-3袖 dan X = 袖+3袖 5. Kurva normal digunakan sebagai acuan pengujian hipotesis jika ukuran sampel n = 30 6. Luas daerah yang dibatasi oleh sumbu-X dan kurva normal sama dengan satu satuan luas.
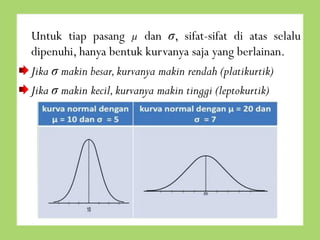
- 5. Untuk tiap pasang 袖 dan , sifat-sifat di atas selalu dipenuhi, hanya bentuk kurvanya saja yang berlainan. Jika makin besar, kurvanya makin rendah (platikurtik) Jika makin kecil, kurvanya makin tinggi (leptokurtik)
- 6. Untuk menentukan peluang harga X antara a dan b, yakni P (a < X < b). b P(a X b) ( 2 ) 1 e 1 x 2 ( ) 2 dx a Untuk penggunaan praktis telah dibuat daftar distribusi normal standar atau normal baku yaitu dengan 袖 = 0 dan = 1 sehingga fungsi densitasnya berbentuk: 1 1 z2 f ( z) e2 2 Untuk z dalam daerah < z < .
- 7. Untuk mengubah distribusi normal umum menjadi distribusi normal baku dapat digunakan menggunakan rumus : Z X Perubahan grafiknya dapat dilihat gambar di bawah ini:
- 8. 1. 2. 3. 4. 5. 6. Setelah distribusi normal baku yang didapat dari distribusi normal umum, maka daftar distribusi normal baku dapat digunakan sehingga bagian-bagian luas distribusi normal baku dapat dicari. Caranya adalah : Hitung z sehingga dua desimal Gambarkan kurvanya seperti gambar normal standar Letakkan harga z pada sumbu datar, lalu tarik garis vertikal hingga memotong kurva. Luas yang tertera dalam daftar adalah luas daerah antara garis ini dengan garis tegak di titik nol. Dalam tabel normal cari tempat harga z pada kolom paling kiri hanya satu desimal dan desimal keduanya dicari pada baris paling atas. Dari z di kolom kiri maju ke kanan dan dari z di baris atas turun ke bawah, maka didapat bilangan yang merupakan luas yang dicari. Bilangan yang didapat harus dituliskan dalam bentuk 0,xxxx (bentuk 4 desimal).
- 9. Contoh penggunaan daftar normal baku yang akan dicari luas daerah, antara lain: 1. Antara z = 0 dan z = 2,15 Gunakan tabel Distribusi Normal. Di bawah z pada kolom kiri cari 2,1 dan di atas sekali cari angka 5. Dari 2,1 maju ke kanan dan 5 menurun, didapat 0,4842. Luas daerah yang dicari, dilihat daerah yang diarsir = 0,4842. 2. Antara z = 0 dan z = -1,86 karena z bertanda negatif, maka pada grafiknya diletakkan di sebelah kiri 0. Untuk daftar digunakan di bawah z kolom kiri didapat 1,8 dan di atas angka 6. Dari 1,8 ke kanan dan dari 6 ke bawah didapat 0,4686 Luas daerah = daerah diarsir = 0,4686.
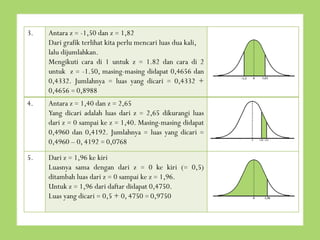
- 10. 3. Antara z = -1,50 dan z = 1,82 Dari grafik terlihat kita perlu mencari luas dua kali, lalu dijumlahkan. Mengikuti cara di 1 untuk z = 1.82 dan cara di 2 untuk z = -1.50, masing-masing didapat 0,4656 dan 0,4332. Jumlahnya = luas yang dicari = 0,4332 + 0,4656 = 0,8988 4. Antara z = 1,40 dan z = 2,65 Yang dicari adalah luas dari z = 2,65 dikurangi luas dari z = 0 sampai ke z = 1,40. Masing-masing didapat 0,4960 dan 0,4192. Jumlahnya = luas yang dicari = 0,4960 0, 4192 = 0,0768 5. Dari z = 1,96 ke kiri Luasnya sama dengan dari z = 0 ke kiri (= 0,5) ditambah luas dari z = 0 sampai ke z = 1,96. Untuk z = 1,96 dari daftar didapat 0,4750. Luas yang dicari = 0,5 + 0, 4750 = 0,9750
- 11. Fenomena distribusi data normal : 1. Kira-kira 68,27% dari kasus ada dalam daerah satu simpangan baku sekitar rata-rata, yaitu antara 袖 dan 袖 + . 2. Ada 95,45% dari kasus terletak dalam daerah dua simpangan baku sekitar rata-rata, yaitu antara 袖 2 dan 袖 + 2 3. Hampir 99,73% dari kasus ada dalam daerah tiga simpangan baku sekitar rata-rata, yaitu antara 袖 3 dan 袖 + 3
- 12. Contoh soal: Berat bayi yang baru lahir rata-rata 3750 gram dengan simpangan baku 325 gram. Jika berat bayi berdistribusi normal, maka tentukan: a. Berapa bayi yang beratnya lebih dari 4500 gram? b. Berapa bayi yang beratnya antara 3500 gram dan 4500 gram, jika semuanya ada 10.000 bayi? c. Berapa bayi yang beratnya lebih kecil atau sama dengan 4000 gram jika semuanya ada 10.000 bayi? d. Berapa bayi yang beratnya 4250 gram jika semuanya ada 5000 bayi?
- 13. Penyelesaian: Dengan X = berat bayi dalam gram, 袖 = 3750 gram, = 325 gram, maka: a. Untuk X = 4500 z X 4500 3750 2,31 325 Berat yang lebih dari 4500 gram, pada grafiknya ada disebelah kanan z = 2,31 Luas daerah ini = 0,5 0,4896 = 0,0104. Jadi, ada 1,04% dari bayi yang beratnya lebih dari 4500 gram
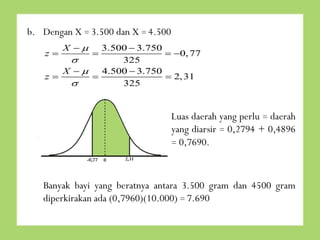
- 14. b. Dengan X = 3500 dan X = 4500 X 3500 3750 0, 77 325 X 4500 3750 z 2, 31 325 z Luas daerah yang perlu = daerah yang diarsir = 0,2794 + 0,4896 = 0,7690. Banyak bayi yang beratnya antara 3500 gram dan 4500 gram diperkirakan ada (0,7960)(10.000) = 7690
- 15. c. Beratnya lebih kecil atau sama dengan 4000 gram, maka beratnya harus lebih kecil dari 4000,5 gram. maka, 4000,5 3750 z 0,77 325 Peluang berat bayi lebih kecil atau sama dengan 4000 gram = 0,5 + 0,2794 = 0,7794. Banyak bayi = (0,7794)(10.000) = 7794 d. Berat 4250 gram berarti antara 4294,5 gram dan 4500,5 gram. Jadi, untuk X = 4294,5 dan X= 4500,5 didapat: 4249, 5 3750 1, 53 325 4250, 5 3750 z 1, 54 325 z Luas daerah yang perlu = 0,4382 0,4370 = 0,0012 Banyak bayi = (0,0012)(5000) = 6
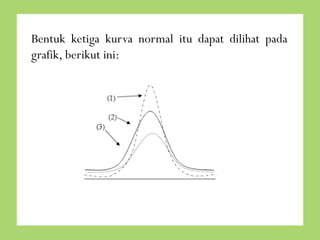
- 16. Jenis bentuk kurva yang diakibatkan oleh perbedaan rentangan nilai dan simpangan baku ada tiga macam: 1. Leptokurtik, merupakan bentuk kurva normal yang meruncing tinggi karena perbedaan frekuensi pada skor-skor yang mendekati rata-rata sangat kecil. 2. Platikurtik, merupakan kurva normal yang mendatar rendah karena perbedaan frekuensi pada skor-skor yang mendekati rata-rata sangat kecil. Skor-skor yang mendekati rata-rata sangat kecil. 3. Normal, merupakan bentuk kurva normal yang biasa, artinya bentuknya merupakan bentuk antara leptokurtik dan platikurtik, karena penyebaran skor biasa dan tidak terjadi kejutan-kejutan yang berarti.
- 17. Bentuk ketiga kurva normal itu dapat dilihat pada grafik, berikut ini: