Distribusi probabilitas
- 2. Variabel Acak Eksperimen probabilitas memiliki keluaran yang dapat berupa nilai numerik, cacahan/hitungan atau hasil pengukuran. Variabel acak, simbol X, deskripsi numerik dari hasil percobaan. X dapat berupa angka apapun tergantung pada keluaran yang mungkin dihasilkan suatu eksperimen. Variabel acak dapat bersifat: 1. Diskrit: Nilai dapat dicacah (countable)/ hasil hitungan 2. Kontinyu: nilai tak terhingga sepanjang interval yang tidak terputus / hasil pengukuran
- 3. Variabel Acak Diskrit Hanya dapat mengambil nilai-nilai tertentu, umumnya dihasilkan dari hasil perhitungan suatu objek Contoh: Jika ada 100 karyawan, maka perhitungan karyawan yang tidak masuk kerja pada hari Senin berada pada nilai-nilai 0,1,2,..100 Percobaan Variabel Acak Kemungkinan Nilai Variabel Acak Penjualan mobil Jenis kelamin pembeli 0 (laki-laki) ; 1 (perempuan) Penelitian 50 produk baru Jumlah produk yang rusak 0,1,2,.., 49, 50 Pencatatan pengunjung toko pada suatu hari Jumlah pengunjung 0,1,2,3,...
- 4. Variabel Acak Kontinyu • Data hasil pengukuran misalnya lebar ruangan, tinggi badan dimana hasil berbeda-beda tergantung pelaku pengukuran dan tingkat ketelitian. • Nilai hasil pengukuran bervariasi dalam suatu selang waktu tertentu Contoh: Jarak antara Jakarta dan Bogor dapat 80km; 80.5 km; Percobaan Variabel Acak Kemungkinan Nilai Variabel Acak Isi botol minuman jadi (maks = 600 ml) Jumlah milimeter 0 ≤ x ≤ 600 Membangun proyek perkantoran baru setelah 6 bulan Persentase proyek diselesaikan 0 ≤ x ≤ 100
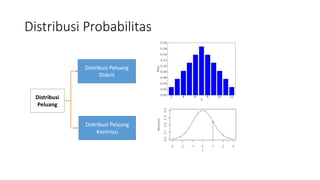
- 5. Distribusi Probabilitas Distribusi Peluang Distribusi Peluang Kontinyu Distribusi Peluang Diskrit
- 6. Distribusi Probabilitas Diskrit Fungsi p(x) yang memberikan nilai peluang untuk setiap variabel X diskrit, dengan syarat: a. 0 ≤ p(x) ≤ 1 b. ∑ p(x) = 1 Distribusi probabilitas dapat disajikan dalam bentuk tabel, grafik, atau rumus.
- 7. Distribusi Probabilitas Diskrit Hasil pengamatan penjualan mobil selama 300 hari pada PT. Caraka. Data yang dicatat adalah jumlah mobil yang terjual dalam sehari Jika X menyatakan jumlah mobil yang terjual dalam sehari, maka: p(0) = probabilitas 0 mobil /hari P(1) = probabilitas 1 mobil /hari Jumlah mobil terjual dalam sehari Jumlah hari 0 54 1 117 2 72 3 42 4 12 5 3
- 8. Dari tabel diperoleh bahwa 54 hari dari 300 hari 0 mobil terjual, dinyatakan 54/300 = 0,18 dan seterusnya ditunjukkan oleh tabel di samping. Dari tabel terlihat peluang 1 mobil terjual dalam sehari adalah 0.39. Jika dihitung probabilitas bahwa 3 mobil atau lebih terjual dalam sehari: P(3) + P(4) + P(5) = 0.14 + 0,04 + 0,01 = 0,19 x p(x) 0 0.18 1 0,39 2 0,24 3 0,14 4 0,04 5 0,01 0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0 1 2 3 4 5 p(x) x Jumlah mobil terjual dalam sehari
- 9. Fungsi Probabilitas Kumulatif Diskrit • Digunakan untuk menyatakan jumlah dari seluruh nilai fungsi probabilitas yang lebih kecil atau sama dengan suatu nilai yang ditetapkan. Contoh: Probabilitas mobil terjual dalam sehari kurang dari atau sama dengan 3 adalah: Jumlahkan probabilitas dari x = 0, x = 1, x = 2, dan x = 3. Jadi P(x ≤ 3) = p(0) + p(1) + p(2) + p(3) = 0.18 + 0.39 + 0.24 + 0.14 = 0.95 x p(x) 0 0.18 1 0,57 (= 0,18 + 0,39) 2 0,81 (= 0,57 + 0,24) 3 0,95 (= 0,81 + 0,14) 4 0,99 (=0,95 + 0,04) 5 1,00 (=0,99 + 0,01)
- 10. Fungsi Probabilitas Kumulatif Diskrit ( ) ( ) ( )F x P X x X p x    ( ) ( )F x P X x  menyatakan fungsi probabilitas kumulatif pada titik X = x yang merupakan jumlah dari seluruh nilai fungsi probabilitas untuk nilai X sama atau kurang dari x
- 11. Distribusi Probabilitas Kontinyu Dinyatakan dengan fungsi f(x) dan sering disebut sebagai fungsi kepadatan probabilitas (density function) Nilai f(x) bisa lebih besar dari 1 Syarat: a. f(x) ≥ 0 b. (integral seluruh fungsi kepadatan probabilitas f(x) = 1 f(x) dx = P {x ≤ X ≤ (x+dx), yaitu probabilitas bahwa nilai X terletak pada interval x dan x+dx ( ) 1f x dx ï‚¥ ï€ï‚¥ 
- 12. Fungsi Probabilitas Kumulatif Kontinyu Nilai-nilai x dalam rumus ini harus kontinyu atau dalam suatu interval ( ) ( ) ( ) x F x P X x f x dx ï€ï‚¥  ï‚£  