1 of 32














Ad
Recommended
1st Mathematics 7 Quiz Bee 2023.pptx
1st Mathematics 7 Quiz Bee 2023.pptxAvilosErgelaKram
?
1. The document outlines the rules and questions for a 1st grade 7 mathematics quiz bee with 4 teams of 14 students each.
2. The contest will include 10 easy questions worth 1 point each, 5 average questions worth 3 points each, and 5 difficult questions worth 5 points each. Questions will be read twice and teams must write their final answer during the allotted time.
3. The questions range from basic arithmetic to simplifying polynomials and cover topics like exponents, coefficients, degrees of polynomials, evaluation, addition/multiplication of polynomials, and word problems. The highest scoring team will be awarded a certificate and extra credit in their final grade.Math10 q2 mod2of8_chords,arcs,central angles and incribe angles of circles_v2...
Math10 q2 mod2of8_chords,arcs,central angles and incribe angles of circles_v2...FahadOdin
?
The document discusses relationships among chords, arcs, central angles, and inscribed angles of circles including defining key terms like radius, diameter, chord, arc and angle types. It explains how to measure arcs in degrees and establishes theorems relating congruent arcs to congruent central angles and chords. The goal is to understand these relationships to solve real-life problems involving circles.LESSON PLAN FOR MATHEMATICS 7.docx
LESSON PLAN FOR MATHEMATICS 7.docxRitchel14
?
This lesson plan outlines teaching measures of central tendency in mathematics. The objectives are to define and identify the mean, median, and mode of statistical data and solve related problems. Students will work in groups on activity sheets involving arranging numbers and identifying the mean, median, or mode. The teacher will distribute worksheets, have students analyze their results, and explain how the tasks relate to the different measures of central tendency. The goal is for students to be able to describe data using mean, median, and mode.Angles of Elevation and Depression -cot.pptx
Angles of Elevation and Depression -cot.pptxRichard Paulino
?
This document outlines a learning module on angles of elevation and depression that was created by Richard B. Paulino. The module includes a PowerPoint presentation, additional activities, outputs from two classes (Goldfish and Grouper), an analysis of results from the Goldfish class, and discussions of challenges encountered and solutions implemented. The module is designed to illustrate angles of elevation and depression and can be integrated into subjects like physics, fish capture, and technical drawing.Inquiry-Based Lesson Plans in Pre-Calculus for Senior High School
Inquiry-Based Lesson Plans in Pre-Calculus for Senior High SchoolGenaro de Mesa, Jr.
?
This document is an inquiry-based lesson plan for pre-calculus covering topics related to angles in a unit circle, including conversions between degree and radian measures, angles in standard position, and coterminal angles. It includes objectives, content areas, learning resources, procedures using problem-based activities, and a philosophical integration about viewing problems from different angles. The plan outlines specific instructional strategies, group activities, and assessment methods for engaging students in understanding circular functions.MATH Lesson Plan sample for demo teaching
MATH Lesson Plan sample for demo teaching preyaleandrina
?
The document outlines a lesson plan focused on teaching students about integers and their operations through various interactive methods including games and group activities. It emphasizes the cognitive, psychomotor, and affective objectives of learning, alongside procedures for classroom management and student engagement. The lesson culminates in an evaluation of student understanding and a reflection on the real-world applications of integers.Mathematics unit plan std. 5
Mathematics unit plan std. 5Edwin López
?
The mathematics unit plan outlines lessons for four weeks. Week one focuses on routines and missing numbers in arithmetic operations. Week two covers fractions, lines/rays, and measurement. Week three addresses fractional parts and linear measurement. Week four involves lines/rays, perimeter, number lines, sequences, scales, and comparing numbers. Lessons incorporate warm-ups, instruction, examples, practice sets, and assessments.introduction to functions grade 11(General Math)
introduction to functions grade 11(General Math)liza magalso
?
This document contains:
1. An outline for a mathematics course covering functions and their graphs, basic business mathematics, and logic.
2. Lessons on identifying functions from relations, evaluating functions, and representing real-life situations using functions including piecewise functions.
3. Examples of evaluating functions, operations on functions, and determining whether a relation is a function based on its graph or ordered pairs.
4. An activity drilling students on identifying functions versus non-functions.General mathematics-function
General mathematics-functionKim Howell Castor
?
This document contains notes from a mathematics lesson on functions. It defines key terms like domain, range, and relation vs. function. It provides examples of different types of functions like piecewise functions and discusses operations that can be performed on functions like addition, subtraction, multiplication, division, and composition. Evaluation of functions at given values and determining if equations represent functions are also covered.Nature of globalisation
Nature of globalisationNagarjun Karnatakam
?
This document discusses the nature, dimensions, reasons, stages and assessment of globalization. It also outlines the merits and demerits of globalization for companies and countries. Specifically, it defines globalization as companies operating across multiple locations linked by common ownership and resources. The dimensions include expanding business globally and developing a global outlook. Reasons for globalization include finding new markets and reducing costs. The stages range from initial exports to fully integrated global operations. The document also discusses the impacts of multinational corporations on host and home countries, as well as some criticisms of multinational corporations.Illustrates permutation -MEGonzalvo.pptx
Illustrates permutation -MEGonzalvo.pptxMaryJaneGonzalvo2
?
Here are the possible arrangements for the situations that illustrate permutations:
1. Arranging 4 different potted plants in a row:
- Plant1, Plant2, Plant3, Plant4
- Plant2, Plant1, Plant3, Plant4
- Plant3, Plant1, Plant2, Plant4
- etc. (4! possible arrangements)
2. Choosing an outfit from 3 blouses and 2 skirts:
- Blouse1, Skirt1
- Blouse1, Skirt2
- Blouse2, Skirt1
- Blouse2, Skirt2
- Blouse3, Skirt1
- Blouse3, Skirt2 (3*Math 7 - Quiz Bee.pptx
Math 7 - Quiz Bee.pptxKristineDeLeon16
?
This document contains 20 multiple choice questions about mathematics concepts such as sets, operations on numbers, fractions, decimals, percentages, measurement, and geometry. The questions cover topics like identifying sets, performing arithmetic operations, converting between fractions and decimals, ordering numbers, calculating percentages, solving word problems involving measurement, and identifying properties of shapes.Shs core general math cg
Shs core general math cgJohndy Ruloma
?
This document outlines the core curriculum for general mathematics for 11th grade students in the Philippines. It covers several key areas of mathematics including functions, rational functions, inverse functions, exponential and logarithmic functions, basic business mathematics concepts like interest and annuities, basic concepts in stocks, bonds and loans, and logic. For each topic, it lists the relevant content and performance standards and provides over 50 specific learning competencies students are expected to master by the end of the course.Evaluating functions basic rules
Evaluating functions basic rulesjulienorman80065
?
This document provides an overview of evaluating functions by giving examples of evaluating functions for given values and providing function rules to evaluate for specific inputs. It emphasizes important rules like exponents, adding and subtracting integers, and order of operations when evaluating functions and provides additional practice problems for readers to evaluate functions based on the given rules.Module 2 polynomial functions
Module 2 polynomial functionsdionesioable
?
This module discusses methods for finding the zeros of polynomial functions of degree greater than 2, including: factor theorem, factoring, synthetic division, and depressed equations. It introduces the number of roots theorem, which states that a polynomial of degree n has n roots. It also discusses determining the rational zeros of a polynomial using the rational roots theorem and factor theorem. Examples are provided to illustrate these concepts and methods.INVERSE FUNCTION
INVERSE FUNCTIONclari1998
?
This lesson plan teaches students about inverse functions. It begins with objectives, materials, and a teaching strategy of lecture. Examples are provided to show how to find the inverse of one-to-one functions by interchanging x and y and solving for the new y. Properties are discussed, such as the inverse of an inverse is the original function. Students are asked to find inverses and solve word problems. The lesson concludes by having students generalize their understanding and complete an evaluation with additional inverse problems.Lesson Plan Sample for Grade 8
Lesson Plan Sample for Grade 8DC Marie Lagura
?
1. The lesson plan discusses relations and functions through classroom activities including a game to demonstrate examples.
2. Key concepts are defined, such as a relation being a set of ordered pairs and a function requiring each domain input to map to only one range output.
3. Examples of both relations that are functions and those that are not are analyzed, with students expected to understand the difference between one-to-one, one-to-many, and many-to-one relations.Rational Functions, Equations, and Inequalities.pptx
Rational Functions, Equations, and Inequalities.pptxJohnlery Guzman
?
This document discusses rational functions, equations, and inequalities. It defines rational expressions as ratios of polynomials and provides examples. Rational equations use equality symbols with rational expressions. Rational inequalities use inequality symbols. Rational functions are functions where both the numerator and denominator are polynomial functions, not including where the denominator is the zero function. The document provides additional examples comparing rational equations, inequalities, and functions.Activity sheets mathematical expressions
Activity sheets mathematical expressionsRuby Rose Ann Panganod
?
The document provides an activity sheet with directions to translate verbal phrases involving an unknown number n into mathematical expressions. It also provides a rubric to evaluate problems formulated and solved involving permutations and combinations that can be observed in real life situations. Students are asked if they have encountered any difficulties formulating real-life problems involving permutations and combinations, and if so, to describe the difficulties.Concept of angle of elevation and depression
Concept of angle of elevation and depressionJunila Tejada
?
This document outlines an activity to help students understand the concepts of angle of elevation and angle of depression. The activity involves students finding classmates at their eye level or taller/shorter, then illustrating tall and short objects outside. They are expected to differentiate elevation and depression angles, link them to real-life contexts, and illustrate the concepts. Key terms like line of sight, elevation angle, and depression angle are defined. Examples are given and students must identify these angles in diagrams. Finally, a math problem applies the elevation angle concept.Exponential Equation & Inequalities.pptx
Exponential Equation & Inequalities.pptxRoqui Gonzaga
?
The document provides instructions for students on exponential equations and inequalities. It defines exponential equations as equations with variable exponents and exponential inequalities as inequalities with exponents that can be solved similarly to equations. Examples of each are provided along with steps to solve them. Students are given problems to solve and informed that an assessment must be completed by midnight.LESSON PLAN IN GRADE 8 MATH FACTORING BY GCMF
LESSON PLAN IN GRADE 8 MATH FACTORING BY GCMFCathyPartidas
?
This document provides a detailed lesson plan for an 8th grade mathematics class on factoring polynomials with common monomial factors. The lesson plan outlines objectives, content, learning resources, procedures, evaluation, and reflection. Key points of the lesson include identifying the greatest common factor of terms, using it to factor polynomials by dividing each term, and applying factoring to solve real-world problems like finding the width of a rectangular garden. Student activities involve practicing identifying common factors, completing factoring problems, and generalizing the factoring process. The teacher evaluates student learning through a multiple choice assessment.Lesson Plan Science 9 August-28-Sept.-1-2023.docx
Lesson Plan Science 9 August-28-Sept.-1-2023.docxarianemiranda17
?
This document contains a daily lesson log for a science teacher teaching lessons about the circulatory and respiratory systems over the course of a week. Each day's objectives are outlined, including content standards, performance standards, and learning competencies. The lessons cover topics like the key parts and functions of the respiratory and circulatory systems, types of circulation, and how the two systems work together to transport gases and molecules through the body. Learning activities are planned each day to reinforce the concepts, and formative assessments are included to evaluate student learning. The teacher reflects on strategies that worked well and difficulties encountered.Logarithmic Functions
Logarithmic Functionsswartzje
?
The document defines logarithmic functions and provides examples of converting between logarithmic and exponential forms. It discusses the properties of logarithmic equality and solving logarithmic equations by rewriting them in exponential form. Key points include: logarithmic and exponential forms are inverses; the exponent becomes the logarithm; logarithmic functions have a domain of positive real numbers; and solving logarithms involves setting arguments equal when bases are the same.Permutation
PermutationAriel Lianko
?
The document discusses permutations and combinations. It defines a permutation as an arrangement of objects where order matters, and a combination as an arrangement where order does not matter. It provides examples of permutations of sets with 3 and 8 elements. The number of permutations of a set of n elements is n factorial. Permutations are arrangements of all elements of a set. The document also provides examples of calculating the number of permutations in different scenarios like seating arrangements and rearrangements of letters in a word.Module functions
Module functionsdionesioable
?
This module introduces functions and how to distinguish them from relations. It discusses:
1) Defining a function and differentiating it from a relation using arrow diagrams and the vertical line test.
2) Identifying the domain and range of a function using sets of ordered pairs.
3) Recognizing functional relationships in real-life situations where one variable depends on another in a one-to-one or many-to-one way.Week5a writing statement of the problem & general purpose 2
Week5a writing statement of the problem & general purpose 2Hafizul Mukhlis
?
This document provides guidance on developing statements of the problem, general purpose, and research questions for a research study. It begins by outlining the learning objectives, which are to discuss and demonstrate understanding of these components, identify language forms used, and formulate sample statements. It emphasizes having an inquisitive mind and questioning attitude. Key questions to consider include the significance of topics, unanswered questions, and feasibility of research. The document provides examples of language for the statement of problem, general purpose, and research questions. It also notes the link between these components and importance of replication studies.Chap 7 Adjusting entries .ppt
Chap 7 Adjusting entries .pptMohamoud9
?
Adjusting entries are journal entries made at the end of an accounting period to ensure revenues and expenses are recorded in the appropriate period. This involves adjusting accounts for accruals, such as unpaid expenses and unrecorded revenue, and deferrals like prepaid expenses and unearned revenue. An adjusted trial balance is prepared after adjusting entries to prove the equality of debit and credit balances before financial statements are made.Uncovering the Mysteries of Black Holes(究極の天体ブラックホールの謎)
Uncovering the Mysteries of Black Holes(究極の天体ブラックホールの謎)Koji Fukuoka
?
Uncovering the Mysteries of the Ultimate Celestial Object, Black HolesMore Related Content
What's hot (20)
General mathematics-function
General mathematics-functionKim Howell Castor
?
This document contains notes from a mathematics lesson on functions. It defines key terms like domain, range, and relation vs. function. It provides examples of different types of functions like piecewise functions and discusses operations that can be performed on functions like addition, subtraction, multiplication, division, and composition. Evaluation of functions at given values and determining if equations represent functions are also covered.Nature of globalisation
Nature of globalisationNagarjun Karnatakam
?
This document discusses the nature, dimensions, reasons, stages and assessment of globalization. It also outlines the merits and demerits of globalization for companies and countries. Specifically, it defines globalization as companies operating across multiple locations linked by common ownership and resources. The dimensions include expanding business globally and developing a global outlook. Reasons for globalization include finding new markets and reducing costs. The stages range from initial exports to fully integrated global operations. The document also discusses the impacts of multinational corporations on host and home countries, as well as some criticisms of multinational corporations.Illustrates permutation -MEGonzalvo.pptx
Illustrates permutation -MEGonzalvo.pptxMaryJaneGonzalvo2
?
Here are the possible arrangements for the situations that illustrate permutations:
1. Arranging 4 different potted plants in a row:
- Plant1, Plant2, Plant3, Plant4
- Plant2, Plant1, Plant3, Plant4
- Plant3, Plant1, Plant2, Plant4
- etc. (4! possible arrangements)
2. Choosing an outfit from 3 blouses and 2 skirts:
- Blouse1, Skirt1
- Blouse1, Skirt2
- Blouse2, Skirt1
- Blouse2, Skirt2
- Blouse3, Skirt1
- Blouse3, Skirt2 (3*Math 7 - Quiz Bee.pptx
Math 7 - Quiz Bee.pptxKristineDeLeon16
?
This document contains 20 multiple choice questions about mathematics concepts such as sets, operations on numbers, fractions, decimals, percentages, measurement, and geometry. The questions cover topics like identifying sets, performing arithmetic operations, converting between fractions and decimals, ordering numbers, calculating percentages, solving word problems involving measurement, and identifying properties of shapes.Shs core general math cg
Shs core general math cgJohndy Ruloma
?
This document outlines the core curriculum for general mathematics for 11th grade students in the Philippines. It covers several key areas of mathematics including functions, rational functions, inverse functions, exponential and logarithmic functions, basic business mathematics concepts like interest and annuities, basic concepts in stocks, bonds and loans, and logic. For each topic, it lists the relevant content and performance standards and provides over 50 specific learning competencies students are expected to master by the end of the course.Evaluating functions basic rules
Evaluating functions basic rulesjulienorman80065
?
This document provides an overview of evaluating functions by giving examples of evaluating functions for given values and providing function rules to evaluate for specific inputs. It emphasizes important rules like exponents, adding and subtracting integers, and order of operations when evaluating functions and provides additional practice problems for readers to evaluate functions based on the given rules.Module 2 polynomial functions
Module 2 polynomial functionsdionesioable
?
This module discusses methods for finding the zeros of polynomial functions of degree greater than 2, including: factor theorem, factoring, synthetic division, and depressed equations. It introduces the number of roots theorem, which states that a polynomial of degree n has n roots. It also discusses determining the rational zeros of a polynomial using the rational roots theorem and factor theorem. Examples are provided to illustrate these concepts and methods.INVERSE FUNCTION
INVERSE FUNCTIONclari1998
?
This lesson plan teaches students about inverse functions. It begins with objectives, materials, and a teaching strategy of lecture. Examples are provided to show how to find the inverse of one-to-one functions by interchanging x and y and solving for the new y. Properties are discussed, such as the inverse of an inverse is the original function. Students are asked to find inverses and solve word problems. The lesson concludes by having students generalize their understanding and complete an evaluation with additional inverse problems.Lesson Plan Sample for Grade 8
Lesson Plan Sample for Grade 8DC Marie Lagura
?
1. The lesson plan discusses relations and functions through classroom activities including a game to demonstrate examples.
2. Key concepts are defined, such as a relation being a set of ordered pairs and a function requiring each domain input to map to only one range output.
3. Examples of both relations that are functions and those that are not are analyzed, with students expected to understand the difference between one-to-one, one-to-many, and many-to-one relations.Rational Functions, Equations, and Inequalities.pptx
Rational Functions, Equations, and Inequalities.pptxJohnlery Guzman
?
This document discusses rational functions, equations, and inequalities. It defines rational expressions as ratios of polynomials and provides examples. Rational equations use equality symbols with rational expressions. Rational inequalities use inequality symbols. Rational functions are functions where both the numerator and denominator are polynomial functions, not including where the denominator is the zero function. The document provides additional examples comparing rational equations, inequalities, and functions.Activity sheets mathematical expressions
Activity sheets mathematical expressionsRuby Rose Ann Panganod
?
The document provides an activity sheet with directions to translate verbal phrases involving an unknown number n into mathematical expressions. It also provides a rubric to evaluate problems formulated and solved involving permutations and combinations that can be observed in real life situations. Students are asked if they have encountered any difficulties formulating real-life problems involving permutations and combinations, and if so, to describe the difficulties.Concept of angle of elevation and depression
Concept of angle of elevation and depressionJunila Tejada
?
This document outlines an activity to help students understand the concepts of angle of elevation and angle of depression. The activity involves students finding classmates at their eye level or taller/shorter, then illustrating tall and short objects outside. They are expected to differentiate elevation and depression angles, link them to real-life contexts, and illustrate the concepts. Key terms like line of sight, elevation angle, and depression angle are defined. Examples are given and students must identify these angles in diagrams. Finally, a math problem applies the elevation angle concept.Exponential Equation & Inequalities.pptx
Exponential Equation & Inequalities.pptxRoqui Gonzaga
?
The document provides instructions for students on exponential equations and inequalities. It defines exponential equations as equations with variable exponents and exponential inequalities as inequalities with exponents that can be solved similarly to equations. Examples of each are provided along with steps to solve them. Students are given problems to solve and informed that an assessment must be completed by midnight.LESSON PLAN IN GRADE 8 MATH FACTORING BY GCMF
LESSON PLAN IN GRADE 8 MATH FACTORING BY GCMFCathyPartidas
?
This document provides a detailed lesson plan for an 8th grade mathematics class on factoring polynomials with common monomial factors. The lesson plan outlines objectives, content, learning resources, procedures, evaluation, and reflection. Key points of the lesson include identifying the greatest common factor of terms, using it to factor polynomials by dividing each term, and applying factoring to solve real-world problems like finding the width of a rectangular garden. Student activities involve practicing identifying common factors, completing factoring problems, and generalizing the factoring process. The teacher evaluates student learning through a multiple choice assessment.Lesson Plan Science 9 August-28-Sept.-1-2023.docx
Lesson Plan Science 9 August-28-Sept.-1-2023.docxarianemiranda17
?
This document contains a daily lesson log for a science teacher teaching lessons about the circulatory and respiratory systems over the course of a week. Each day's objectives are outlined, including content standards, performance standards, and learning competencies. The lessons cover topics like the key parts and functions of the respiratory and circulatory systems, types of circulation, and how the two systems work together to transport gases and molecules through the body. Learning activities are planned each day to reinforce the concepts, and formative assessments are included to evaluate student learning. The teacher reflects on strategies that worked well and difficulties encountered.Logarithmic Functions
Logarithmic Functionsswartzje
?
The document defines logarithmic functions and provides examples of converting between logarithmic and exponential forms. It discusses the properties of logarithmic equality and solving logarithmic equations by rewriting them in exponential form. Key points include: logarithmic and exponential forms are inverses; the exponent becomes the logarithm; logarithmic functions have a domain of positive real numbers; and solving logarithms involves setting arguments equal when bases are the same.Permutation
PermutationAriel Lianko
?
The document discusses permutations and combinations. It defines a permutation as an arrangement of objects where order matters, and a combination as an arrangement where order does not matter. It provides examples of permutations of sets with 3 and 8 elements. The number of permutations of a set of n elements is n factorial. Permutations are arrangements of all elements of a set. The document also provides examples of calculating the number of permutations in different scenarios like seating arrangements and rearrangements of letters in a word.Module functions
Module functionsdionesioable
?
This module introduces functions and how to distinguish them from relations. It discusses:
1) Defining a function and differentiating it from a relation using arrow diagrams and the vertical line test.
2) Identifying the domain and range of a function using sets of ordered pairs.
3) Recognizing functional relationships in real-life situations where one variable depends on another in a one-to-one or many-to-one way.Week5a writing statement of the problem & general purpose 2
Week5a writing statement of the problem & general purpose 2Hafizul Mukhlis
?
This document provides guidance on developing statements of the problem, general purpose, and research questions for a research study. It begins by outlining the learning objectives, which are to discuss and demonstrate understanding of these components, identify language forms used, and formulate sample statements. It emphasizes having an inquisitive mind and questioning attitude. Key questions to consider include the significance of topics, unanswered questions, and feasibility of research. The document provides examples of language for the statement of problem, general purpose, and research questions. It also notes the link between these components and importance of replication studies.Chap 7 Adjusting entries .ppt
Chap 7 Adjusting entries .pptMohamoud9
?
Adjusting entries are journal entries made at the end of an accounting period to ensure revenues and expenses are recorded in the appropriate period. This involves adjusting accounts for accruals, such as unpaid expenses and unrecorded revenue, and deferrals like prepaid expenses and unearned revenue. An adjusted trial balance is prepared after adjusting entries to prove the equality of debit and credit balances before financial statements are made.More from Koji Fukuoka (20)
Uncovering the Mysteries of Black Holes(究極の天体ブラックホールの謎)
Uncovering the Mysteries of Black Holes(究極の天体ブラックホールの謎)Koji Fukuoka
?
Uncovering the Mysteries of the Ultimate Celestial Object, Black Holesトポロジーが語る声明のかたち(The shape of life revealed by topology)
トポロジーが語る声明のかたち(The shape of life revealed by topology)Koji Fukuoka
?
The shape of life revealed by topology生成AIベンダー最新ニュース(Latest news from gen-AI vendors)2025/1
生成AIベンダー最新ニュース(Latest news from gen-AI vendors)2025/1Koji Fukuoka
?
Latest news from generative AI vendors量子計算が紡ぐ新しい宇宙像(A New Cosmic Perspective Woven by Quantum Computing)
量子計算が紡ぐ新しい宇宙像(A New Cosmic Perspective Woven by Quantum Computing)Koji Fukuoka
?
A New Cosmic Perspective Woven by Quantum Computing生成AIでヒトの知能探究を加速化する(Accelerating the exploration of human intelligence with ge...
生成AIでヒトの知能探究を加速化する(Accelerating the exploration of human intelligence with ge...Koji Fukuoka
?
Accelerating the exploration of human intelligence with generative AIAd
ゲノム(顿狈础)解析で浮かびあがる古代からの日本列岛の谜(2024年3月17日)
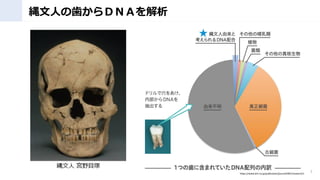
- 4. 全体の流れ 1. 古代ゲノム解析の基礎 2. ゲノム解析で浮かびあがる日本人 1. 日本列島への移住ルート 2. 縄文人とは? 3. 日本人のルーツ 3. まとめ 4
- 6. 最新科学で人類考古学(日本列島)をUpdate 6 https://i-bioarchaeology.org/research/ 統合生物考古学(integrative bioarchaeology)の概念図 領域代表 山田 康弘 東京都立大学 人文科学研究科 教授
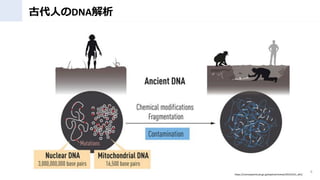
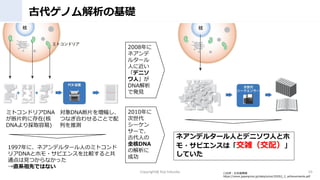
- 10. 古代ゲノム解析の基礎 Copyright@ Koji fukuoka 10 〇出所:日本国際賞 https://www.japanprize.jp/data/prize/2020/j_2_achievements.pdf ミトコンドリアDNA が断片的に存在(核 DNAより採取容易) 対象DNA断片を増幅し、 つなぎ合わせることで配 列を推測 1997年に、ネアンデルタール人のミトコンド リアDNAとホモ?サピエンスを比較すると共 通点は見つからなかった →直系祖先ではない 2010年に 次世代 シーケン サーで、 古代人の 全核DNA の解析に 成功 ネアンデルタール人とデニソワ人とホ モ?サピエンスは「交雑(交配)」 していた 2008年に ネアンデ ルタール 人に近い 「デニソ ワ人」が DNA解析 で発見
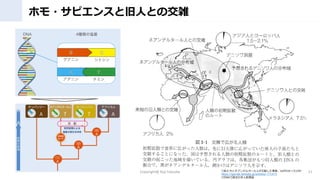
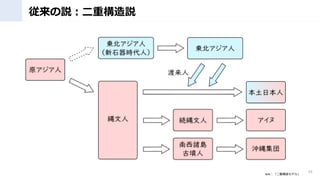
- 11. ホモ?サピエンスと旧人との交雑 Copyright@ Koji fukuoka 11 〇私たちとネアンデルタール人が交配した事実、なぜわかったのか https://gendai.ismedia.jp/articles/-/71473 〇DNAで語る日本人起源論
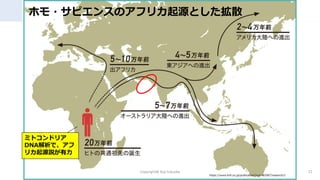
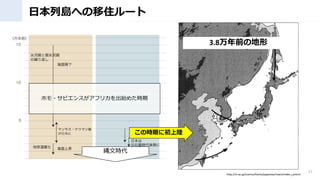
- 12. ホモ?サピエンスのアフリカ起源とした拡散 Copyright@ Koji fukuoka 12 https://www.brh.co.jp/publication/journal/087/research/1 ミトコンドリア DNA解析で、アフ リカ起源説が有力
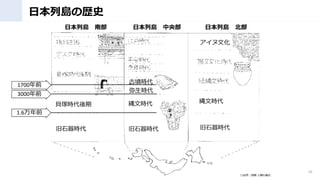
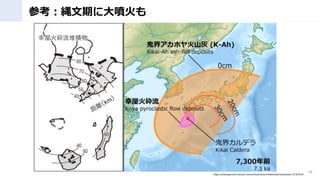
- 16. 日本列島の歴史 16 〇出所:図解 人類の進化 1.6万年前 3000年前 1700年前 貝塚時代後期 縄文時代 弥生時代 縄文時代 旧石器時代 旧石器時代 旧石器時代 古墳時代 アイヌ文化 日本列島 南部 日本列島 中央部 日本列島 北部
- 26. 独自の発展を遂げた縄文時代:縄文土器 26 深鉢形土器(火焔型土器) 縄文中期 新潟県十日町市笹山遺跡出土 十日町 市博物館蔵 国宝 Wiki:「縄文土器」 縄文土器 世界でも最古級(1.6万年前)の土器が青森県 大台山本遺跡で発見 ※世界最古は中国で2022年に発表された2万 年前の土器片 中期になると左図のように独特な修飾を施し たものも。 https://www.nikkei.com/article/DGXNASDG2803Y_Y2A620C1CR8000 https://jomon-japan.jp/kids/learn/map/odai-yamamoto/ 大台山本(おおだ い やまもと)遺跡 の 無文土器片 (むもんどきへん)
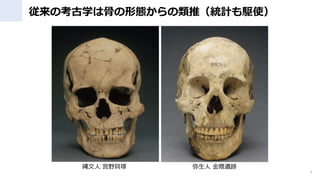
- 27. 縄文?弥生時代人の復元 27 船泊遺跡(北海道礼文島)で出土した 縄文人女性の復元(約3800年前) https://www.nikkei.com/article/DGXMZO65930200W0A101C2MY1000/ https://www.yomiuri.co.jp/pluralphoto/20211031-OYT1I50015/ 青谷 上寺地 ( かみじち ) 遺跡(鳥取 県鳥取市)で出土した弥生人の復元
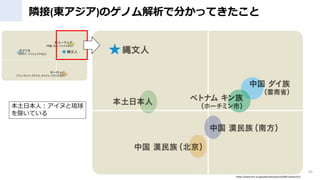
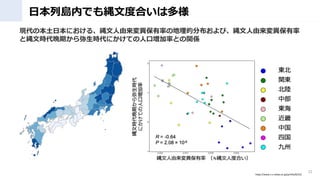
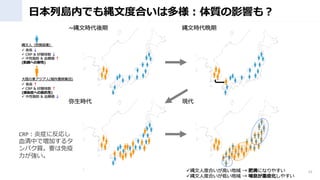
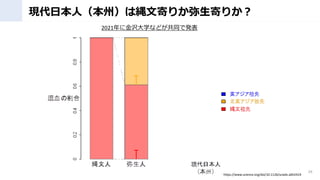
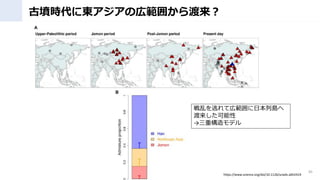
- 32. まとめ ? ゲノム解析含む最新科学が考古学を大幅にUpdate ? 日本列島に4万年前に渡ってきた縄文人は近隣の大陸人と異な る独自DNAを持っていた(ただし列島内で多様) ? 現代日本人のDNAは、縄文?弥生よりも、古墳時代に東アジア から渡来したDNAが濃いことが分かり、注目が集まっている。 32
