DTGP AAIP11
- 1. Veri?ed Stack-based Genetic Programming via Dependent Types by Larry Diehl Tuesday, July 19, 2011
- 2. Motivation ? avoid searching space of stack under/ over?owing programs ? use strongly typed genetic operators ? avoid logic and runtime errors due to increasingly complex genetic operators ? use a total and dependently typed language Tuesday, July 19, 2011
- 3. Dependent Types ? Agda programming language ? purely functional (like Haskell) ? total (coverage/termination/positivity) ? types can encode any intuitionistic logic formula ? e.g. proof theory judgement ˇ°Even 6ˇ± Tuesday, July 19, 2011
- 4. Genetic Programming ? representation ? genetic operators ? evaluation function ? initialization procedure Tuesday, July 19, 2011
- 5. ˇ°Forthˇ± operations word consumes produces true 0 1 not 1 1 and 2 1 Tuesday, July 19, 2011
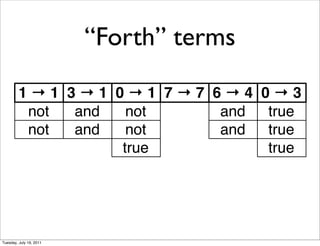
- 6. ˇ°Forthˇ± terms 1ˇú1 3ˇú1 0ˇú1 7ˇú7 6ˇú4 0ˇú3 not and not and true not and not and true true true Tuesday, July 19, 2011
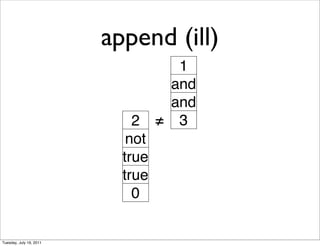
- 7. append (ill) 1 and and 2 ˇŮ 3 not true true 0 Tuesday, July 19, 2011
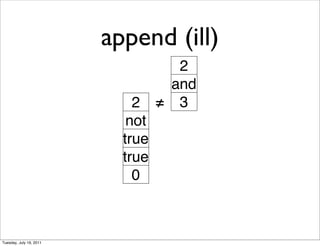
- 8. append (ill) 2 and 2 ˇŮ 3 not true true 0 Tuesday, July 19, 2011
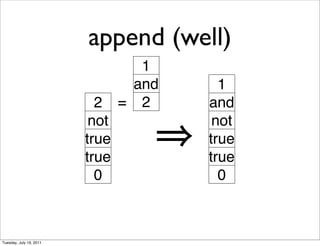
- 9. append (well) 1 and 1 2 = 2 and not not true true true true 0 0 Tuesday, July 19, 2011
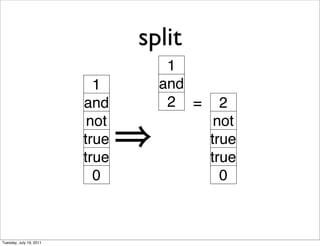
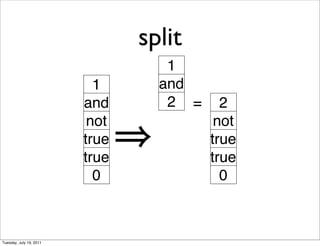
- 10. split 1 1 and and 2 = 2 not not true true true true 0 0 Tuesday, July 19, 2011
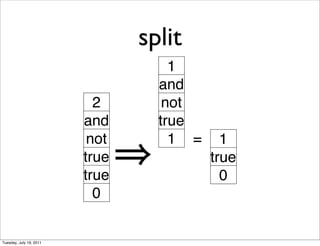
- 11. split 1 and 2 not and true not 1 = 1 true true true 0 0 Tuesday, July 19, 2011
- 12. Agda Crash Course Tuesday, July 19, 2011
- 13. data Bool : Set where true false : Bool data ? : Set where zero : ? suc : ? ! ? one : ? one = suc zero two : ? two = suc one three : ? three = suc two Tuesday, July 19, 2011
- 14. data List (A : Set) : Set where [] : List A _ˇË_ : A ! List A ! List A falseˇË[] : List Bool falseˇË[] = false ˇË [] trueˇËfalseˇË[] : List Bool trueˇËfalseˇË[] = true ˇË falseˇË[] Tuesday, July 19, 2011
- 15. data Vec (A : Set) : ? ! Set where [] : Vec A zero _ˇË_ : {n : ?} ! A ! Vec A n ! Vec A (suc n) falseˇË[]1 : Vec Bool one falseˇË[]1 = false ˇË [] trueˇËfalseˇË[]2 : Vec Bool two trueˇËfalseˇË[]2 = true ˇË falseˇË[]1 Tuesday, July 19, 2011
- 16. _+_ : ? ! ? ! ? zero + n = n suc m + n = suc (m + n) _++_ : {A : Set} {m n : ?} ! Vec A m ! Vec A n ! Vec A (m + n) [] ++ ys = ys (x ˇË xs) ++ ys = x ˇË (xs ++ ys) trueˇËfalseˇËtrueˇË[]3 : Vec Bool three trueˇËfalseˇËtrueˇË[]3 = (true ˇË false ˇË []) ++ (true ˇË []) Tuesday, July 19, 2011
- 17. Representation Tuesday, July 19, 2011
- 18. data Word : Set where true not and : Word data List (A : Set) : Set where [] : List A _ˇË_ : A ! List A ! List A Term = List Word Tuesday, July 19, 2011
- 19. bc : Term -- 2 1 bc = and ˇË [] ab : Term -- 0 2 ab = not ˇË true ˇË true ˇË [] ac : Term -- 0 1 ac = and ˇË not ˇË true ˇË true ˇË [] Tuesday, July 19, 2011
- 20. bc : Term 2 1 bc = and [] ab : Term 0 2 ab = not (true (true [])) ac : Term 0 1 ac = and (not (true (true []))) Tuesday, July 19, 2011
- 21. data Term (inp : ?) : ? ! Set where [] : Term inp inp true : {out : ?} ! Term inp out ! Term inp (1 + out) not : {out : ?} ! Term inp (1 + out) ! Term inp (1 + out) and : {out : ?} ! Term inp (2 + out) ! Term inp (1 + out) Tuesday, July 19, 2011
- 22. module DTGP {Word : Set} (pre post : Word ! ? ! ?) where data Term (inp : ?) : ? ! Set where [] : Term inp inp _ˇË_ : ? {n} (w : Word) ! Term inp (pre w n) ! Term inp (post w n) Tuesday, July 19, 2011
- 23. data Word : Set where true not and : Word pre : Word ! ? ! ? pre true n = n pre not n = 1 + n pre and n = 2 + n post : Word ! ? ! ? post true n = 1 + n post not n = 1 + n post and n = 1 + n open import DTGP pre post Tuesday, July 19, 2011
- 24. bc : Term 2 1 bc = and ˇË [] ab : Term 0 2 ab = not ˇË true ˇË true ˇË [] ac : Term 0 1 ac = and ˇË not ˇË true ˇË true ˇË [] Tuesday, July 19, 2011
- 25. Genetic Operators Tuesday, July 19, 2011
- 26. crossover : {inp out : ?} (female male : Term inp out) (randF randM : ?) ! Term inp out ˇÁ Term inp out Tuesday, July 19, 2011
- 27. bc : Term 2 1 bc = and ˇË [] ab : Term 0 2 ab = not ˇË true ˇË true ˇË [] ac : Term 0 1 ac = bc ++ ab Tuesday, July 19, 2011
- 28. _++_ : ? {inp mid out} ! Term mid out ! Term inp mid ! Term inp out [] ++ ys = ys (x ˇË xs) ++ ys = x ˇË (xs ++ ys) Tuesday, July 19, 2011
- 29. split 1 1 and and 2 = 2 not not true true true true 0 0 Tuesday, July 19, 2011
- 30. ac : Term 0 1 ac = and ˇË not ˇË true ˇË true ˇË [] bc++ab : Split 2 ac bc++ab = bc ++' ab Tuesday, July 19, 2011
- 31. data Split {inp out} mid : Term inp out ! Set where _++'_ : (xs : Term mid out) (ys : Term inp mid) ! Split mid (xs ++ ys) Tuesday, July 19, 2011
- 32. ac : Term 0 1 ac = and ˇË not ˇË true ˇË true ˇË [] bc++ab : Split 2 ac bc++ab = proj? (split 1 ac) Tuesday, July 19, 2011
- 33. ac : Term 0 1 ac = and ˇË not ˇË true ˇË true ˇË [] bc++ab : ¦˛ ? ¦Ë mid ! Split mid ac bc++ab = split 1 ac Tuesday, July 19, 2011
- 34. split : ? {inp out} (n : ?) (xs : Term inp out) ! ¦˛ ? ¦Ë mid ! Split mid xs split zero xs = _ , [] ++' xs split (suc n) [] = _ , [] ++' [] split (suc n) (x ˇË xs) with split n xs split (suc n) (x ˇË .(xs ++ ys)) | _ , xs ++' ys = _ , (x ˇË xs) ++' ys Tuesday, July 19, 2011
- 35. Evaluation Function Tuesday, July 19, 2011
- 36. bc : Term 2 1 bc = and ˇË [] eval-bc : Vec Bool 1 eval-bc = eval bc (true ˇË false ˇË []) ac : Term 0 1 ac = and ˇË not ˇË true ˇË true ˇË [] eval-ac : Vec Bool 1 eval-ac = eval ac [] Tuesday, July 19, 2011
- 37. eval : {inp out : ?} ! Term inp out ! Vec Bool inp ! Vec Bool out eval [] is = is eval (true ˇË xs) is = true ˇË eval xs is eval (not ˇË xs) is with eval xs is ... | o ˇË os = ? o ˇË os eval (and ˇË xs) is with eval xs is ... | o? ˇË o? ˇË os = (o? ˇÄ o?) ˇË os Tuesday, July 19, 2011
- 38. score : Term 0 1 ! ? score xs with eval xs [] ... | true ˇË [] = 0 ... | false ˇË [] = 1 open Evolution score Tuesday, July 19, 2011
- 39. Initialization Procedure Tuesday, July 19, 2011
- 40. choices : List Word choices = true ˇË not ˇË and ˇË [] population : List (Term 0 1) population = init 2 0 1 choices -- (and ˇË true ˇË true ˇË []) ˇË -- (not ˇË not ˇË true ˇË []) ˇË -- (not ˇË true ˇË []) ˇË -- (true ˇË []) ˇË -- [] Tuesday, July 19, 2011
- 41. -- data Term (inp : ?) : ? ! Set where -- _ˇË_ : ? {n} (w : Word) ! -- Term inp (pre w n) ! -- Term inp (post w n) -- pre : Word ! ? ! ? -- pre and n = 2 + n trueˇËtrue : Term 0 2 trueˇËtrue = true ˇË true ˇË [] andˇËandˇËtrue : Term 0 1 andˇËandˇËtrue = _ˇË_ {n = 0} and trueˇËtrue Tuesday, July 19, 2011
- 42. match : (w : Word) (out : ?) ! Dec (¦˛ ? ¦Ë n ! out ˇÔ pre w n) match true n = yes (n , refl) match not zero = no ?p where ?p : ¦˛ ? (¦Ë n ! 0 ˇÔ suc n) ! ˇÍ ?p (_ , ()) match not (suc n) = yes (n , refl) Tuesday, July 19, 2011
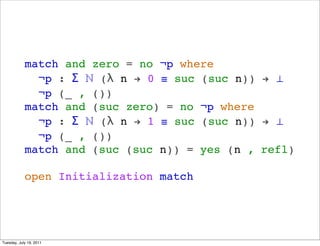
- 43. match and zero = no ?p where ?p : ¦˛ ? (¦Ë n ! 0 ˇÔ suc (suc n)) ! ˇÍ ?p (_ , ()) match and (suc zero) = no ?p where ?p : ¦˛ ? (¦Ë n ! 1 ˇÔ suc (suc n)) ! ˇÍ ?p (_ , ()) match and (suc (suc n)) = yes (n , refl) open Initialization match Tuesday, July 19, 2011
- 44. Generalization Tuesday, July 19, 2011
- 45. module DTGP {Domain Word : Set} (pre post : Word ! Domain ! Domain) (_?_ : (x y : Domain) ! Dec (x ˇÔ y)) where data Term (inp : Domain) : Domain ! Set where [] : Term inp inp _ˇË_ : ? {d} (w : Word) ! Term inp (pre w d) ! Term inp (post w d) Tuesday, July 19, 2011
- 46. data Word : Set where not gt : Word num : ? ! Word record Domain : Set where constructor _,_ field bools : ? nats : ? postulate _?_ : (x y : Domain) ! Dec (x ˇÔ y) Tuesday, July 19, 2011
- 47. pre : Word ! Domain ! Domain pre not (m , n) = 1 + m , n pre (num _) (m , n) = m , n pre gt (m , n) = m , 2 + n post : Word ! Domain ! Domain post not (m , n) = 1 + m , n post (num _) (m , n) = m , 1 + n post gt (m , n) = 1 + m , n open DTGP pre post _?_ Tuesday, July 19, 2011
- 48. bc : Term (0 , 2) (1 , 0) bc = not ˇË gt ˇË [] ab : Term (0 , 0) (0 , 2) ab = num 3 ˇË num 5 ˇË [] ac : Term (0 , 0) (1 , 0) ac = bc ++ ab Tuesday, July 19, 2011
- 49. FIN github.com/larrytheliquid/dtgp/tree/aaip11 questions? Tuesday, July 19, 2011








![data List (A : Set) : Set where
[] : List A
_ˇË_ : A ! List A ! List A
falseˇË[] : List Bool
falseˇË[] = false ˇË []
trueˇËfalseˇË[] : List Bool
trueˇËfalseˇË[] = true ˇË falseˇË[]
Tuesday, July 19, 2011](https://image.slidesharecdn.com/diehl-aaip-pres-111122231423-phpapp02/85/DTGP-AAIP11-14-320.jpg)
![data Vec (A : Set) : ? ! Set where
[] : Vec A zero
_ˇË_ : {n : ?} !
A ! Vec A n ! Vec A (suc n)
falseˇË[]1 : Vec Bool one
falseˇË[]1 = false ˇË []
trueˇËfalseˇË[]2 : Vec Bool two
trueˇËfalseˇË[]2 = true ˇË falseˇË[]1
Tuesday, July 19, 2011](https://image.slidesharecdn.com/diehl-aaip-pres-111122231423-phpapp02/85/DTGP-AAIP11-15-320.jpg)
![_+_ : ? ! ? ! ?
zero + n = n
suc m + n = suc (m + n)
_++_ : {A : Set} {m n : ?} !
Vec A m ! Vec A n ! Vec A (m + n)
[] ++ ys = ys
(x ˇË xs) ++ ys = x ˇË (xs ++ ys)
trueˇËfalseˇËtrueˇË[]3 : Vec Bool three
trueˇËfalseˇËtrueˇË[]3 =
(true ˇË false ˇË []) ++ (true ˇË [])
Tuesday, July 19, 2011](https://image.slidesharecdn.com/diehl-aaip-pres-111122231423-phpapp02/85/DTGP-AAIP11-16-320.jpg)

![data Word : Set where
true not and : Word
data List (A : Set) : Set where
[] : List A
_ˇË_ : A ! List A ! List A
Term = List Word
Tuesday, July 19, 2011](https://image.slidesharecdn.com/diehl-aaip-pres-111122231423-phpapp02/85/DTGP-AAIP11-18-320.jpg)
![bc : Term -- 2 1
bc = and ˇË []
ab : Term -- 0 2
ab = not ˇË true ˇË true ˇË []
ac : Term -- 0 1
ac = and ˇË not ˇË true ˇË true ˇË []
Tuesday, July 19, 2011](https://image.slidesharecdn.com/diehl-aaip-pres-111122231423-phpapp02/85/DTGP-AAIP11-19-320.jpg)
![bc : Term 2 1
bc = and []
ab : Term 0 2
ab = not (true (true []))
ac : Term 0 1
ac = and (not (true (true [])))
Tuesday, July 19, 2011](https://image.slidesharecdn.com/diehl-aaip-pres-111122231423-phpapp02/85/DTGP-AAIP11-20-320.jpg)
![data Term (inp : ?) : ? ! Set where
[] : Term inp inp
true : {out : ?} !
Term inp out !
Term inp (1 + out)
not : {out : ?} !
Term inp (1 + out) !
Term inp (1 + out)
and : {out : ?} !
Term inp (2 + out) !
Term inp (1 + out)
Tuesday, July 19, 2011](https://image.slidesharecdn.com/diehl-aaip-pres-111122231423-phpapp02/85/DTGP-AAIP11-21-320.jpg)
![module DTGP
{Word : Set}
(pre post : Word ! ? ! ?)
where
data Term (inp : ?) : ? ! Set where
[] : Term inp inp
_ˇË_ : ? {n} (w : Word) !
Term inp (pre w n) !
Term inp (post w n)
Tuesday, July 19, 2011](https://image.slidesharecdn.com/diehl-aaip-pres-111122231423-phpapp02/85/DTGP-AAIP11-22-320.jpg)

![bc : Term 2 1
bc = and ˇË []
ab : Term 0 2
ab = not ˇË true ˇË true ˇË []
ac : Term 0 1
ac = and ˇË not ˇË true ˇË true ˇË []
Tuesday, July 19, 2011](https://image.slidesharecdn.com/diehl-aaip-pres-111122231423-phpapp02/85/DTGP-AAIP11-24-320.jpg)


![bc : Term 2 1
bc = and ˇË []
ab : Term 0 2
ab = not ˇË true ˇË true ˇË []
ac : Term 0 1
ac = bc ++ ab
Tuesday, July 19, 2011](https://image.slidesharecdn.com/diehl-aaip-pres-111122231423-phpapp02/85/DTGP-AAIP11-27-320.jpg)
![_++_ : ? {inp mid out} !
Term mid out !
Term inp mid !
Term inp out
[] ++ ys = ys
(x ˇË xs) ++ ys = x ˇË (xs ++ ys)
Tuesday, July 19, 2011](https://image.slidesharecdn.com/diehl-aaip-pres-111122231423-phpapp02/85/DTGP-AAIP11-28-320.jpg)
![ac : Term 0 1
ac = and ˇË not ˇË true ˇË true ˇË []
bc++ab : Split 2 ac
bc++ab = bc ++' ab
Tuesday, July 19, 2011](https://image.slidesharecdn.com/diehl-aaip-pres-111122231423-phpapp02/85/DTGP-AAIP11-30-320.jpg)

![ac : Term 0 1
ac = and ˇË not ˇË true ˇË true ˇË []
bc++ab : Split 2 ac
bc++ab = proj? (split 1 ac)
Tuesday, July 19, 2011](https://image.slidesharecdn.com/diehl-aaip-pres-111122231423-phpapp02/85/DTGP-AAIP11-32-320.jpg)
![ac : Term 0 1
ac = and ˇË not ˇË true ˇË true ˇË []
bc++ab : ¦˛ ? ¦Ë mid ! Split mid ac
bc++ab = split 1 ac
Tuesday, July 19, 2011](https://image.slidesharecdn.com/diehl-aaip-pres-111122231423-phpapp02/85/DTGP-AAIP11-33-320.jpg)
![split : ? {inp out} (n : ?)
(xs : Term inp out) !
¦˛ ? ¦Ë mid ! Split mid xs
split zero xs = _ , [] ++' xs
split (suc n) [] = _ , [] ++' []
split (suc n) (x ˇË xs) with split n xs
split (suc n) (x ˇË .(xs ++ ys))
| _ , xs ++' ys = _ , (x ˇË xs) ++' ys
Tuesday, July 19, 2011](https://image.slidesharecdn.com/diehl-aaip-pres-111122231423-phpapp02/85/DTGP-AAIP11-34-320.jpg)

![bc : Term 2 1
bc = and ˇË []
eval-bc : Vec Bool 1
eval-bc = eval bc (true ˇË false ˇË [])
ac : Term 0 1
ac = and ˇË not ˇË true ˇË true ˇË []
eval-ac : Vec Bool 1
eval-ac = eval ac []
Tuesday, July 19, 2011](https://image.slidesharecdn.com/diehl-aaip-pres-111122231423-phpapp02/85/DTGP-AAIP11-36-320.jpg)
![eval : {inp out : ?} ! Term inp out !
Vec Bool inp ! Vec Bool out
eval [] is = is
eval (true ˇË xs) is = true ˇË eval xs is
eval (not ˇË xs) is with eval xs is
... | o ˇË os = ? o ˇË os
eval (and ˇË xs) is with eval xs is
... | o? ˇË o? ˇË os = (o? ˇÄ o?) ˇË os
Tuesday, July 19, 2011](https://image.slidesharecdn.com/diehl-aaip-pres-111122231423-phpapp02/85/DTGP-AAIP11-37-320.jpg)
![score : Term 0 1 ! ?
score xs with eval xs []
... | true ˇË [] = 0
... | false ˇË [] = 1
open Evolution score
Tuesday, July 19, 2011](https://image.slidesharecdn.com/diehl-aaip-pres-111122231423-phpapp02/85/DTGP-AAIP11-38-320.jpg)

![choices : List Word
choices = true ˇË not ˇË and ˇË []
population : List (Term 0 1)
population = init 2 0 1 choices
-- (and ˇË true ˇË true ˇË []) ˇË
-- (not ˇË not ˇË true ˇË []) ˇË
-- (not ˇË true ˇË []) ˇË
-- (true ˇË []) ˇË
-- []
Tuesday, July 19, 2011](https://image.slidesharecdn.com/diehl-aaip-pres-111122231423-phpapp02/85/DTGP-AAIP11-40-320.jpg)
![-- data Term (inp : ?) : ? ! Set where
-- _ˇË_ : ? {n} (w : Word) !
-- Term inp (pre w n) !
-- Term inp (post w n)
-- pre : Word ! ? ! ?
-- pre and n = 2 + n
trueˇËtrue : Term 0 2
trueˇËtrue = true ˇË true ˇË []
andˇËandˇËtrue : Term 0 1
andˇËandˇËtrue = _ˇË_ {n = 0} and trueˇËtrue
Tuesday, July 19, 2011](https://image.slidesharecdn.com/diehl-aaip-pres-111122231423-phpapp02/85/DTGP-AAIP11-41-320.jpg)


![module DTGP
{Domain Word : Set}
(pre post : Word ! Domain ! Domain)
(_?_ : (x y : Domain) ! Dec (x ˇÔ y))
where
data Term (inp : Domain) : Domain ! Set where
[] : Term inp inp
_ˇË_ : ? {d} (w : Word) !
Term inp (pre w d) !
Term inp (post w d)
Tuesday, July 19, 2011](https://image.slidesharecdn.com/diehl-aaip-pres-111122231423-phpapp02/85/DTGP-AAIP11-45-320.jpg)


![bc : Term (0 , 2) (1 , 0)
bc = not ˇË gt ˇË []
ab : Term (0 , 0) (0 , 2)
ab = num 3 ˇË num 5 ˇË []
ac : Term (0 , 0) (1 , 0)
ac = bc ++ ab
Tuesday, July 19, 2011](https://image.slidesharecdn.com/diehl-aaip-pres-111122231423-phpapp02/85/DTGP-AAIP11-48-320.jpg)
