economic channel section
- 1. MOST ECONOMICAL CHANNEL SECTION: APPLICABILITY TO RECTANGULAR AND TRAPEZOIDAL CHANNELS MADE BY : VAIBHAV PATHAK MECHANICAL B.TECH 3 YEAR
- 2. UNIFORM FLOW IN OPEN CHANNELS Definitions ?a) Open Channel: Duct through which Liquid Flows with a Free Surface - River, Canal ?b) Steady and Non- Steady Flow: In Steady Flows, all the characteristics of flow are constant with time. In unsteady flows, there are variations with time.
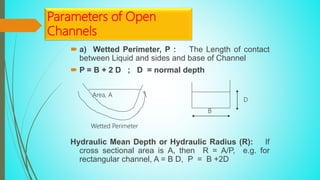
- 3. Parameters of Open Channels ? a) Wetted Perimeter, P : The Length of contact between Liquid and sides and base of Channel ? P = B + 2 D ; D = normal depth Hydraulic Mean Depth or Hydraulic Radius (R): If cross sectional area is A, then R = A/P, e.g. for rectangular channel, A = B D, P = B +2D Area, A Wetted Perimeter D B
- 4. Empirical Flow Equations for Estimating Normal Flow Velocities ? a) Chezy Formula (1775): Can be derived from basic principles. It states that: ; ? Where: V is velocity; R is hydraulic radius and S is slope of the channel. C is Chezy coefficient and is a function of hydraulic radius and channel roughness. SRCV ?
- 5. Definitions ?a) Freeboard: Vertical distance between the highest water level anticipated in the design and the top of the retaining banks. It is a safety factor to prevent the overtopping of structures. ?b) Side Slope (Z): The ratio of the horizontal to vertical distance of the sides of the channel. Z = e/d = e¨/D
- 6. DESIGN OF CHANNELS FOR STEADY UNIFORM FLOW ? Channels are very important in Engineering projects especially in Irrigation and, Drainage. ? Channels used for irrigation are normally called canals ? Channels used for drainage are normally called drains.
- 7. MOST EFFICIENT SECTION During the design stages of an open channel, the channel cross-section, roughness and bottom slope are given. The objective is to determine the flow velocity, depth and flow rate, given any one of them. The design of channels involves selecting the channel shape and bed slope to convey a given flow rate with a given flow depth. For a given discharge, slope and roughness, the designer aims to minimize the cross-sectional area A in order to reduce construction costs
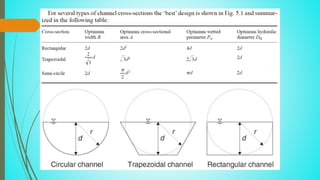
- 8. The most `efficient¨ cross-sectional shape is determined for uniform flow conditions. Considering a given discharge Q, the velocity V is maximum for the minimum cross-section A. According to the Manning equation the hydraulic diameter is then maximum. It can be shown that: 1.the wetted perimeter is also minimum, 2.the semi-circle section (semi-circle having its centre in the surface) is the best hydraulic section Because the hydraulic radius is equal to the water cross section area divided by the wetted parameter, Channel section with the least wetted parameter is the best hydraulic section
- 9. RECTANGULAR SECTION For a rectangular section Q=AV, where Q=discharge through the channel, A=area of flow. V=velocity with which water is flowing in the channel. For Q to be maximum ,V needs to be maximum, Since A = constant. But V=C?mi Where m= hydraulic mean depth. i= bed slope. m=A/P where P=wetted perimeter. For m to be maximum ,P ?minimum
- 10. A=BD ?B=A/D; P=B+2D ,then P=A/D+2D ?? ?? = ?? ?2 + 2 ?? ?? = 0 ?? ?2 + 2 = 0 ?2 = ? 2 = ?? 2 D = ? 2 ? = ?? ? + 2? = 2?2 2? + 2? = ? 2 ? = ? 2
- 11. TRAPEZOIDAL SECTION For a rectangular section Q=AV, where Q=discharge through the channel, A=area of flow. V=velocity with which water is flowing in the channel. For Q to be maximum ,V needs to be maximum, Since A = constant. But V=C?mi Where m= hydraulic mean depth. i= bed slope. m=A/P where P=wetted perimeter. For m to be maximum ,P ?minimum
- 12. ? = ?? + ??2 ? = ? + 2? 1 + ?2 ? = ? ? ? ??2 ? = ? ? ? ?? ? = ? ? ? ?? + 2? 1 + ?2 ?? ?? = ?? ?2 ? ? + 2 1 + ?2 ?? ?? = 0, ? ?? ?2 ? ? + 2 1 + ?2 = 0 2 1 + ?2 = ? + ? ?2 2 1 + ?2 = ? + ?? ?2 + ? ? ? = 2( 1 + ?2 ? ? ? + 2?? 2 = ? 1 + ?2 CONCLUSION: HALF OF THE TOP WIDTH = SIDE WALL LENGTH
- 13. m = D/2 The best side slope for Trapezoidal section ? ? = ? ? ? ?? + 2? 1 + ?2 ?? ?? = 0 ? ? + 2? 2 1 + ?2 ? 2? ? ? ? ? = 0 ? = 1 〔 3 ? = 600
- 15. open channel as shown Q=10m3/s, velocity =1.5m/s, for most economic section. find wetted parameter, and the bed slope n=0.014. Trapezoidal Example 4 ? ? mD DDDA DkDBA m V Q A BD DB D kDB kD 78.1 667.6) 2 3 6055.0( 667.6 5.1 10 6055.0 2 2 32 2 31 2 2 1 2 2 2 ? ???? ?? ??? ? ?? ?? ? ??
- 16. mP kDDP kDBP 49.7 2 3 178.12)78.1(6055.0 126055.0 12 2 2 2 ?? ? ? ? ? ? ????? ??? ??? To calculate bed Slope 6.1941:1 5.189.0 014.0 1 89.0 49.7 667.6 m49.7 m667.6 1 3 2 2 3 2 ? ??? ??? ? ? ? S SV P A R P A SR n V h h