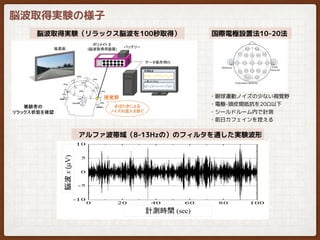
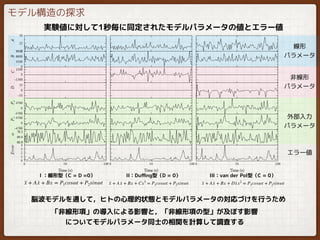
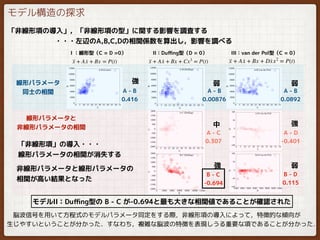
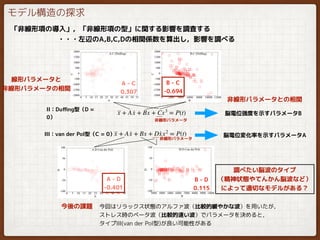
EEG analysis (nonlinear)
- 1. 臨床生体医療工学ラボ中間報告資料 Date : 20181019 EEG Group 上原 賢祐 (D2) ?脳波の利用応用 ?脳波の解析と事情 (どこまで分かっててこれから何をすべきか) ?本研究の具体的な狙いと進捗 ?まとめと今後の展開 コンテンツ ヒトの状態推定をするために 脳波の時系列データを如何にモデリングするか? 脳波解析界隈の周辺研究と比較した 本研究の立ち位置と価値
- 2. 脳波とは神経細胞の活動電位 EEG: ElectroEncephaloGram ECoG: ElectroCoticoGram 頭皮上電位 皮質上電位 二つの違いを比べる EEG ECoG 取得コスト 低 高 侵襲性 無 有 信号明瞭さ 低 高 ±10 ~ 100 μV (noise) -80 ~ +40 mV [1] [1] 脳波の謎:リズムとその存在理由,良峯徳和,多摩大学研究紀要「経営情報研究」,No21 (2017) pp. 93-100. 減衰
- 3. 脳波とは神経細胞の活動電位 EEG: ElectroEncephaloGram ECoG: ElectroCoticoGram 頭皮上電位 皮質上電位 二つの違いを比べる EEG ECoG 取得コスト 低 高 侵襲性 無 有 信号明瞭さ 低 高 ±10 ~ 100 μV (noise) -80 ~ +40 mV [1] [1] 脳波の謎:リズムとその存在理由,良峯徳和,多摩大学研究紀要「経営情報研究」,No21 (2017) pp. 93-100. EEG vs ECoG どの分野でどのように利用したいかによって決まる 脳波 2 脳波 コミュニケーション (カーツワイル) エンタメ 感情推定Necomimi, Neurowear, Japan, O?cial video 電脳世界 診断 BMI スタンフォード大学による麻痺患者の応用例 Christine Lowe Having an Epileptic Seizure (Graphic) 減衰
- 4. 脳波解析を如何にして行うか OUTPUTによって適切な解析方法がある ?(時間)周波数解析 ?加算平均,移動平均法 ?独立成分分析 ◎リアプノフ指数の計算 ◎相関次元解析 ◎位相平面 信号処理による解析 モデル化による解析 (時系列 or 周波数 or more) 線形 非線形 ?線形モデル ◎非線形モデル
- 5. OUTPUT:個人差を考慮しないヒトの状態推定 脳波信号の処理 → 時間周波数解析(最強) 頭部14channelの計測可 (Emotiv EPOC+, EMOTIV, San Francisco, U.S.A ) 周波数解析により状態区別が可能 ただ解析アルゴリズム(BlackBox)非公開なため研究者として気になる 各種状態が数値化されて 表示される Necomimi, Neurowear, Japan, O?cial video [2] Time Frequency analysis of Olfactory induced EEG-power change, V. Alexander, et al., PLOS biomaterial, https://doi.org/10.1371/journal.pone.0185596 (2017) pp.1-11. [3] Toward an?EEG-based recognition of music liking using time-frequency?analysis, SK Hadjidimitriou, IEEE Transaction on Biomedical, Vol. 52, Issue 12 (2012) pp. 3498 - 3510. 現状,特定の強い感覚刺激(匂い&音 and MORE)に対しては 時間周波数解析でも論文がアクセプトされている状況[2, 3]. 周波数解析のみでいくのはレッドオーシャン(病理は除く) コンシューマ用途では ほぼ100%FFTが用いられる 7月に購入しました!
- 6. OUTPUT:ブレインマシンインターフェース(BMI)の実装!? 脳波信号の処理 → 加算平均,独立成分分析 [4] Eog/Erp Hybrid Human-Machine Interface For Robot Control, Jiaxin Ma, Yu Zhang, Yunjun Nam, Andrzej Cichocki And Fumitoshi Matsuno, Proc. Ieee/Rsj International Conference On Intelligent Robots And Systems (Iros2013), Pp.859-864, 2013. Kyoto Univ., Matsuno Lab, Mechatronics Lab. [4] 加算平均,独立成分分析,ERP(Event Relativ Potencial) Sの視覚刺激に対して300 msec後に, 頭頂部でマイナス電位が見られる Tの低頻度刺激では反射が遅れる ?特定の刺激を用意する必要がある ?装置が大掛かり. ?個人差によるためパーソナライズ ?もちろん感情は分からない デメリットとERPの課題
- 7. 脳波解析を如何にして行うか OUTPUTによって適切な解析方法がある ?(時間)周波数解析 ?加算平均,移動平均法 ?独立成分分析 ◎リアプノフ指数の計算 ◎相関次元解析 ◎位相平面 信号処理による解析 モデル化による解析 (時系列 or 周波数 or more) 線形 非線形 ?線形モデル ◎非線形モデル 脳波の振る舞いは非線形である ヒトの感情推定を行う際は こっちが主流 アウトプットによっては 線形処理でも良い
- 8. リアプノフ指数???時系列軌道の安定性をみる h = Δx0 f(x0 + h) ? f(x0) = Δx1 f′(x0) f′(x0) = lim h→0 f(x0 + h) ? f(x0) h x0 x0 + h Δx2 = f′(x1)Δx1 初期値 のズレが に 拡大(縮小)したとすると Δx0 Δx1 OUTPUT:脳波の裏側にある秩序を知りたい(ヒトの状態との紐付け) Δx1 = f′(x0)Δx0 Δx2 = f′(x1)f′(x0)Δx0 Δxn = f′(xn?1)f′(xn?2)?f′(x1)f′(x0)Δx0 初期値 のズレがn番目には 以上のように拡大(or縮小)されてる Δx0 Δxn Δx0 = enλ log Δxn Δx0 = nλ λ = lim x→∞ 1 n n?1 ∑ i=0 log| f′(x)| enλ λ は e のべき乗であったので, 正 → 指数関数的に軌道の拡大率が増加(カオス) 負 → 軌道が単調という指標 時系列波形のカオス性を確認したい場合は, 以上の反復計算を行って,リアプノフ指数を確認 すれば良い
- 9. OUTPUT:脳波の裏側にある秩序を知りたい(ヒトの状態との紐付け) 脳波信号の処理 → 非線形解析(リアプノフ指数,相関次元など) 脳波は非線形性(カオス性)が認められていて,線形解析では厳密に解けない Δxn Δx0 = enλ λリアプノフ指数 ??? 指数が正を返せば“カオス” を含んでいるとされる.しか しランダムノイズでも“正”を 返す場合もある の軌道に対する の離れ度合いx0 xn λ = lim x→∞ 1 n n?1 ∑ i=1 log| f′(x)| リラックス脳波 100 sec ストレス脳波 100sec Sampling 0.002 sec 実験データは最近アクセプト された論文のものを使用 [5] 解析窓 = 1秒間 500 sample (1秒ごとのカオスを計測) [5]上原賢祐,齊藤俊,”カオス性を持つヒト脳波の非線形ダイナミクスに着目した解析手法の提案”, 日本機械学会論文集,Vol.84, No.864 (2018.8), pp.18-00218. 集中時の脳波の方が,リアプノフ指数が全体的に大 きく,カオス的に振る舞うことが確認された 予測: リラックス状態の方が,カオス度合いが大きいと 予測していたが,それとは異なる 単純に軌道安定性の観点から,波形が”カオス”と いうものを示唆するだけで,カオス度合いは明確 には測れないのか? アルファ波 [8 -13 Hz]
- 10. OUTPUT:脳波の裏側にある秩序を知りたい(ヒトの状態との紐付け) カオス解析???リアプノフ指数 文献調査や,脳波信号の対象による調査など細かいことを実施. ?他の研究者が類似の調査をしてないか? ?てんかんの状態ではどうか? ?脳波以外の生体信号ではどうか? → おおよそ10以下の正の値 → 上昇する(5~8) → 指先脈波で正となる? (脳波と同様) Answer てんかん脳波の場合 (ch1, ch2に注目) 指先脳波でも脳波と同様な値を観測[6] [6]前田優輔,鈴木平,”問題解決における思考リズムの変容ーダイナミカルシステム?アプローチの観点からー”,桜美林大学心理学研究, Vol.7 (2016), pp.117-130. 脳波解析の分野ではカオスの確認はこれで良しとされているものの, 未だ確定的に値の議論はされてなく,何かしらの参考材料程度で扱われている指標
- 11. OUTPUT:脳波の裏側にある秩序を知りたい(ヒトの状態との紐付け) 脳波信号の処理 → 非線形解析(リアプノフ指数,相関次元など) 相関次元??時系列データに隠されたアトラクタ構造を取る次元をみる x v x x sin wave 時系列データの変位-速度の プロットをして見ると何かしらの 状態が見てくるのでは はたして,2次元空間でそれが記述できるのか? 3次元,4次元,???more が必要ではないのか? カオスの次元 = 非整数 [7] [7]池口徹,山田泰司,小室元政,”カオス時系列の基礎と応用”,産業図書,(2002). t
- 12. OUTPUT:脳波の裏側にある秩序を知りたい(ヒトの状態との紐付け) 脳波信号の処理 → 非線形解析(リアプノフ指数,相関次元など) 相関次元 D2???時系列データに隠されたアトラクタをみる [8]合原一幸,”ニューラルシステムにおけるカオス”,東京電気大学出版社,(1993). 相関次元のデータセットを作成 [8] Xi Xj = (x1, x2, ?xm) Xj Xj r データセットを m次元空間にプロット 注目するベクトル と他ベクトル の距離XjXi 相関次元は,あるベクトルを中心に,その他周辺ベクトルが存在する確率piを単純に積分で解いたもの ?Xj |Xi| pi = 1 N N ∑ j=1 H(r ? |Xi ? Xj |) H(r ? |Xi ? Xj |) = 0, r < |Xi ? Xj | H(r ? |Xi ? Xj |) = 1, r ≧ |Xi ? Xj | 確率 ヘビサイド関数 D2 = lim r→0 log C(r) log r (C(r) ≡ N ∑ i=1 p2 i ) 相関次元 m:次元 τ:時間遅れ
- 13. OUTPUT:脳波の裏側にある秩序を知りたい(ヒトの状態との紐付け) 脳波信号の処理 → 非線形解析(リアプノフ指数,相関次元など) 相関次元???時系列データに隠されたアトラクタをみる D2 = lim r→0 log C(r) log r 脳波データに対して 相関次元をみる m:3次元 τ:0.02sの時間遅れ 相関次元は 図の傾きを観察 3.5 2. 9 カオスに存在する複雑な秩序を推定する ための有効自由度の探索 リラックス状態の方がよりカオス的で, アトラクタを捉えるために必要な相関次元は3.5 複雑な時系列データの複雑度合いを示すことができる
- 14. 相関次元の更なる探求 3.5次元で脳波のある秩序を記述することが可能か? m次元の相関次元を導出 (左:リラックス 右:ストレス) m: 3次元 τ: 0.02sの時間遅れ 例えば,埋め込み次元を変化させると… ストレス時の方が 傾きが大きくなる 有効自由度が増す m: 5次元 τ: 0.02s 相関次元の解決できていない問題 偽の相関次元値 ?スケーリングの問題,総データ数 ?傾きをどこで取るか定義が はっきりしてない ?算出された有効次元を再度 図示する手法がない ビッグデータを収集して, まとめ上げるのが現在主流だったりする [8]合原一幸,”ニューラルシステムにおけるカオス”,東京電気大学出版社,(1993). これまで明らかにされている相関次元の例[8]
- 15. OUTPUT:脳波の裏側にある秩序を知りたい(ヒトの状態との紐付け) 脳波信号の処理 → 非線形解析(リアプノフ指数,相関次元など) <上記の具体的な諸問題> ?系全体の複雑性は観察できるが,実測波形の細かい変動を追わないので, ヒトの精神的,生理的なもので変動する脳波の根本的な結びつけが困難である 相関次元 アトラクタ(時間発展の郡)の任意の点における半径 r と その径内に含まれる他アトラクタの構成点を数える カオスに存在する複雑な秩序を推定するための有 効自由度の探索 C(r) :相関積分 直線部の傾き値が 相関次元に対応する m:埋め込み次元 (アトラクタ次元) 従来されている非線形(カオス)解析では,カオスの存在は確認する ことは可能であるが,ヒトの状態を推定する目的では!? Δxn Δx0 = enλ リアプノフ指数 指数が正を返せば“カオス”を含んでいるとされる しかしランダムノイズでも“正”を返す場合もある の軌道に対する の離れ度合いxnx0 D2 = lim r→0 ∑ N i=1 C(r) log r [5]上原賢祐,齊藤俊,”カオス性を持つヒト脳波の非線形ダイナミクスに着目した解析手法の提案”,日本機械学会論文集,Vol.84, No.864 (2018.8), pp.18-00218. λ = lim x→∞ 1 n n?1 ∑ i=1 log| f′(x)|
- 16. 脳波解析を如何にして行うか OUTPUTによって適切な解析方法がある ?(時間)周波数解析 ?加算平均,移動平均法 ?独立成分分析 ◎リアプノフ指数の計算 ◎相関次元解析 ◎位相平面 信号処理による解析 モデル化による解析 (時系列 or 周波数 or more) 線形 非線形 ?線形モデル ◎非線形モデル 脳波解析界隈の周辺研究と比べて 本研究の目指すところは? 脳波の振る舞いは非線形である ヒトの感情推定を行う際は こっちが主流 アウトプットによっては 線形処理でも良い 目的を達成するには, 対象を深く観察する ことが大事なのでは
- 17. モデル化による解析 (時系列 or 周波数 or more) 脳波の解析と事情 線形 VS 非線形 ???明らかにしたい内容によって作り上げるべき ヒトの生理的,精神的な状態を推定する xn = M ∑ i=1 aixn?1 + ?n x1, x2, x3?xn時系列データ 例えば ARモデル(Autoregressive model) xn = a1xn?1 + a2xn?2 + a3xn?3 + ? + ?n a1xn?1 a2xn?2 a3xn?3 xn 一つ先を予測するために, どういったパラメータを 決めるのか? 自己の前の値を重み付け(パラメータ)して足し合わせて,それにちょっとしたノイズを入れる a1, a2, a3?, an, ?n :未知なパラメータ x1, x2, x3?xn :既知なパラメータ 現象に合うようなパラメータを推定する必要があるが,これで脳波の挙動が記述できる か?
- 18. モデル化による解析 (時系列 or 周波数 or more) 線形 VS 非線形 ???明らかにしたい内容によって作り上げるべき ヒトの生理的,精神的な状態を推定する 脳波の解析と事情 2005 ARモデルがよく使われてた[9][10][11] 非線形モデルが主流 [10]西田茂人,他4名,”脳波モデルを用いた優位律動の特徴表現と背景脳波の自動判定”,生体医工学会,Vol.43, No.3 (2005), pp.447-455. xn = 4 ∑ i=1 aixn?1 sin(2πminΔt) + bi sin(2πminΔt) + ?n 脳波の振る舞いに特化したARモデル[10] [9]深見忠典,他4名,”局所定常自己回帰モデルを用いた脳波特徴波検出”,電気学会論文誌,Vol.122, No.9 (2002), pp.1553-1559. [11]Gelareh M.,et al,”Person Identi?cation by Using AR model for EEG Signal”,Proceedings of World Academy of Science and Technology,Vol.11, ISSN 1307-6884 (2006), pp.281-285. 2010 線形 VS 非線形 論争[12][13] 非線形モデルの方が, 波形フィット率およびパラメータの意味づけの面で軍配 パラメータ同定の困難さの向上[12][13] [12]Parham G.,et al,”Stochastic Dynamic Modeling of the Human Brain EEG Signal”,ASME 2013 Dynamic Systems and Control Conference,Vol.2, No.DSCC2013-3881 (2013), pp.V002T22A003. [13]上原賢祐,齊藤俊,”脳波信号を対象としたEPIAモデル構造に関する研究”,Dynamics and Design Conference 2018, No.18-7, 283 (2018.8)
- 19. 本研究の狙いと進捗について ヒトの生理的,精神的状態を見るために 脳波の時系列データを如何にモデリングするか? カオス性を有する脳波は不規則的な振る舞いをする → ある臨界時間以下であれば定量的な解析が可能? ··x + A ·x + Bx + Cx3 = P1cosωt + P2sinωt 線形項 非線形振動子:粘性減衰振動系 + Du?ng型の非線形項 非線形項 外部入力項 <モデリングの根拠> ?脳波の変動機序は決定論的カオスに従う ? 確率的要素を内包せずに,初期状態から未来の状態が一意に記述できる [14] [14]Ben. H. Janson, “Quantitative analysis of electroencephalograms: is there chaos in the future?”, International journal of bio-medical computing, No.95-123, (1991). 狙い:初期値(x0, v0)を与えて,ある解析窓ごとにモデルパラメータを 脳波変動に合うように同定すると状態推定が可能になる
- 20. 本研究の狙いと進捗について ヒトの生理的,精神的状態を見るために 脳波の時系列データを如何にモデリングするか? 脳波の変動機序は決定論的カオスに従う[14] ?未来の状態が記述できる ?しかし,初期値によってt→∞の値が大きく異なる ··x + A ·x + Bx + Cx3 = P1cosωt + P2sinωt脳波の非線形振る舞いモデル A = 13.0 B = 3994.0 C = 1297.0 ω = 61.0 初期位置 = 0.0 初期速度(紫) = 1.0 初期速度(緑) = 1.1 P1 = 800.0 P2 = 1500.0 0.1の初速の差で20秒後には 完全に波形が合わなくなる 今回のモデルが脳波に適している と考えられる大きな理由の一つである パラメータをある時間窓ごとに 実験的に同定していくことで 状態推定が可能では(EPIA)
- 21. 本研究の狙いと進捗について(ちょっと詳しく研究の核を紹介) ヒトの生理的,精神的状態を見るために 脳波の時系列データを如何にモデリングするか? -10 -5 0 5 10 ··x + A ·x + Bx + Cx3 = P1cosωt + P2sinωt脳波の非線形振る舞いモデル: なるほど,こういう挙動になるのか 経験値が上がったぞ! よし,そしたらもっと剛性をあげてみよう パラメータ(A,B,C)を 与えた時の xの挙動を見て考察する -10 -5 0 5 10 Experimental Simulation 1 sec. xという目的があり, それに合うように パラメータ(A,B,C)を決める 同定された値は,実際の脳波挙動を 数値的に示したものであるから, ヒトの状態を推定できるであろう!
- 22. モデルパラメータの同定手法に関して 解析窓(1秒)とパラメータ同定を行うためのError関数について 1秒毎にパラメータ同定 ··x + A ·x + Bx + Cx3 = P1cosωt + P2sinωt 解析窓を1秒に設定し,モデルのシミュレーション値と実験値のError関数が 最小になるようにパラメータの同定を行う Error(A, B, C, D, P1, P2 . ω) = 1 N N ∑ i=1 (xexp i ? xsim i )2 以上の最小値問題を解くために,実数型GAを用いているが 乱数により初期パラメータを振りまくった方がエラー値が小さくなるので, 内側のアルゴリズムは割愛
- 23. リラックス VS ストレス脳波の検討 リラックス脳波 100 sec ストレス脳波 100sec Sampling 0.002 sec 解析窓 = 1秒間 500 sample アルファ波 [8 -13 Hz] リラックス ストレス リラックス,ストレス脳波ともに, 実測値の振る舞いに一致している ことが分かる ヒトの状態を推定 ··x + A ·x + Bx + Cx3 = P1cosωt + P2sinωt
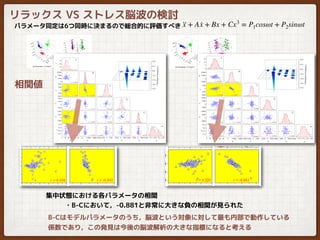
- 24. リラックス VS ストレス脳波の検討 ヒトの状態推定を行うために各パラメータ値の調査 ··x + A ·x + Bx + Cx3 = P1cosωt + P2sinωt リラックス時とストレス時の違いを数値的にみる 平均値 ?非線形パラメータ C が極端に低下 (30.2倍) ?線形パラメータのバネ定数 B は増加(1.37倍) ?線形パラメータのダンピング定数 A は微増(1.1倍) ? ? 集中状態になると 集中状態になると,これまでカオス的に活動していた脳活動が線形的になる [5] しかしながら,この結果の解釈は容易であるが,従来のカオス解析とは異なる [5]上原賢祐,齊藤俊,”カオス性を持つヒト脳波の非線形ダイナミクスに着目した解析手法の提案”,日本機械学会論文集,Vol.84, No.864 (2018.8), pp.18-00218.
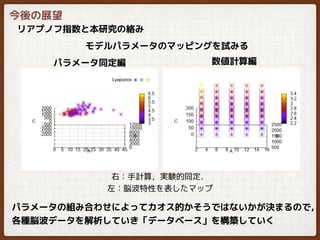
- 25. リラックス VS ストレス脳波の検討 ··x + A ·x + Bx + Cx3 = P1cosωt + P2sinωt 相関値 パラメータ同定は6つ同時に決まるので総合的に評価すべき ?B-Cにおいて,-0.881と非常に大きな負の相関が見られた 集中状態における各パラメータの相関 B-Cはモデルパラメータのうち,脳波という対象に対して最も内部で動作している 係数であり,この発見は今後の脳波解析の大きな指標になると考える
- 26. まとめ ヒトの生理的,精神的状態を見るために 脳波の時系列データを如何にモデリングするか? ··x + A ·x + Bx + Cx3 = P1cosωt + P2sinωt脳波の非線形振る舞いモデル ?非線形パラメータ C が極端に低下 (30.2倍) ?線形パラメータのバネ定数 B は増加(1.37倍) ?線形パラメータのダンピング定数 A は微増(1.1倍) ? ? 集中状態になると,各パラメータの値は? ?B-Cにおいて,-0.881と非常に大きな負の相関を確認. 集中状態になると,各パラメータの相関?
- 27. 今後の展望 ヒトの生理的,精神的状態を見るために 脳波の時系列データを如何にモデリングするか? ··x + A ·x + Bx + Cx3 = P1cosωt + P2sinωt脳波の非線形振る舞いモデル 脳波のモデルとして主張するため以下が必要である ?多種多様な脳波データを調べる ?モデルパタメータに意味づけを行う ?自由度と変数の数の再考察 ?従来のカオス解析とハイブリッドで定量化できないかを考える ?解析窓1秒からの拡大(目標3秒) ?アルファ波以外の検討 ?多点脳波の影響の検討 また,以上を成し遂げるためにも パラメータ同定アルゴリズムの改良は欠かせない GAの組み直し,機械学習の導入 etc.
- 30. Parameter Correlation A - Lyapunov -0.2525 B - Lyapunov 0.08739 C - Lyapunov -0.2499 リアプノフ指数と本研究の絡み モデルパラメータのマッピングを試みる 今後の展望
- 32. パラメータ同定解析窓の延長 (2秒)[15] [15]上原賢祐,齊藤俊,”非線形振動子を用いた脳波モデルの精度検証”,日本機械学会関西支部92期定時総会講演会,M416 ,No.174-1 (2017.3).
- 33. パラメータ同定解析窓の延長 (2秒)[15] [15]上原賢祐,齊藤俊,”非線形振動子を用いた脳波モデルの精度検証”,日本機械学会関西支部92期定時総会講演会,M416 ,No.174-1 (2017.3).
- 34. パラメータ同定解析窓の延長 (2秒)[15] [15]上原賢祐,齊藤俊,”非線形振動子を用いた脳波モデルの精度検証”,日本機械学会関西支部92期定時総会講演会,M416 ,No.174-1 (2017.3).
- 37. モデルパラメータ?変数の考察
- 38. <実験的にモデルパラメータを定めることについての問題> ?複数のモデルパラメータを同時に求めるので,組み合わせによっ ては系の現象を説明できない可能性がある. 系の現象を説明できるパラメータの意味づけのためにも,これまで扱っ ていたDu?ng型のモデルだけではなく,他の振動子モデルを使用した値 との比較は今度の重要な知見になりうる ··x + A ·x + Bx + Cx3 = P1cosωt + P2sinωt <EPIAを確立するための必要な課題> 多種多様な実験値を用いて調査 脳波に適したモデルの自由度 や変数の数などを調査 ··x + A ·x + Bx + Cx3 = P1cosωt + P2sinωt ··x + A ·x + Bx + D··xx2 = P1cosωt + P2sinωt ? ? モデル根本の組み立て 仮説や予測を必要とするもの モデルを決めて 脳波に対するモデルパラメータを同定 相互に調べる 必要がある 今後の展望(モデル再興)
- 39. 脳波信号を対象とした EPIAモデル構造に関する研究 ··x + A ·x + Bx + (C + 1 3 D d dt )x3 = P1cosωt + P2sinωt ベースのモデル 非線形項線形項 外部入力項 モデル 方程式 I :線形型(C = D =0) II:Du?ng型(D = 0) III:van der Pol型(C = 0) ··x + A ·x + Bx = P1cosωt + P2sinωt ··x + A ·x + Bx + Cx3 = P1cosωt + P2sinωt ··x + A ·x + Bx + D·xx2 = P1cosωt + P2sinωt モデルパラメータ {A,B,C,D,P1,P2, }の7つを解析窓ごとに同定する変数として扱う 脳波モデルを通して,ヒトの心理的状態とモデルパラメータの対応づけを行うため 「非線形項」の導入による影響 「非線形項の型」が及ぼす影響 <三種類の方程式を調査する狙い> ω モデル構造の探求
- 40. ?共振で動作する機械システムの圧電エネルギーハーベスタ 振動周波数を共振に持って行くときに,共振ピークの歪みが非線形的なので, DUFFING振動子を用いて予測や解析がなされている. Geal Sebald, et al. ”Experimental Duffing oscillator for broadband piezoelectric energy haryesting”, Smart Materials and Structures, vol. 20, 102001, (2011) pp.1-10 ··x + A ·x + Bx + Cx3 = P1cosωt + P2sinωt ··x + A ·x + Bx + D·xx2 = P1cosωt + P2sinωt Du?ng型 van der Pol型 ?脳血管病変の同定に使用 血流,血管,脳組織,これらを単一とした非線形な回路を提案している. 脳血管循環系の数学モデルを用いて血管病変部位の調査をしている D. V. Parshin, et al. ”Differential properties of Van Der Pol - Duffing mathematical model of cerebrovascu hemodynamics based on clinical measurements”, Nonlinear Waves: Theory and New Application (Wave16) IOP Published Journal of Physics, 722, 012030 (2016) pp.1-6. 脳波信号を対象とした EPIAモデル構造に関する研究 モデル構造の探求 参考リファレンス
- 41. ··x + A ·x + Bx = P1cosωt + P2sinωt I :線形型(C = D =0) ··x + A ·x + Bx + Cx3 = P1cosωt + P2sinωt ··x + A ·x + Bx + D ·xx2 = P1cosωt + P2sinωt II:Du?ng型(D = 0) III:van der Pol型(C = 0) 線形 パラメータ 非線形 パラメータ 外部入力 パラメータ エラー値 実験値に対して1秒毎に同定されたモデルパラメータの値とエラー値 脳波モデルを通して,ヒトの心理的状態とモデルパラメータの対応づけを行うため 「非線形項」の導入による影響と,「非線形項の型」が及ぼす影響 についてモデルパラメータ同士の相関を計算して調査する モデル構造の探求
- 42. モデル構造の探求 「非線形項の導入」,「非線形項の型」に関する影響を調査する ???左辺のA,B,C,Dの相関係数を算出し,影響を調べる ··x + A ·x + Bx = P(t) I :線形型(C = D =0) ··x + A ·x + Bx + Cx3 = P(t) ··x + A ·x + Bx + D ·xx2 = P(t) II:Du?ng型(D = 0) III:van der Pol型(C = 0) 線形パラメータ 同士の相関 線形パラメータと 非線形パラメータの相関 A - B 0.416 A - B 0.00876 A - B 0.0892 A - C 0.307 A - D -0.401 B - D 0.115 B - C -0.694 弱 強 モデルII:Du?ng型の B - C が-0.694と最も大きな相関値であることが確認された 中 弱 弱 強 強 脳波信号を用いて方程式のモデルパラメータ同定をする際,非線形項の導入によって,特徴的な傾向が 生じやすいということが分かった.すなわち,複雑な脳波の特徴を表現しうる重要な項であることが分かった. 非線形パラメータと線形パラメータの 相関が高い結果となった 「非線形項」の導入??? 線形パラメータの相関が消失する
- 43. モデル構造の探求 「非線形項の導入」,「非線形項の型」に関する影響を調査する ???左辺のA,B,C,Dの相関係数を算出し,影響を調べる 線形パラメータと 非線形パラメータの相関 A - C 0.307 A - D -0.401 B - D 0.115 B - C -0.694 ··x + A ·x + Bx + Cx3 = P(t) ··x + A ·x + Bx + D·xx2 = P(t) II:Du?ng型(D = 0) III:van der Pol型(C = 0) 非線形パラメータ 非線形パラメータ 今回はリラックス状態のアルファ波(比較的緩やかな波)を用いたが, ストレス時のベータ波(比較的速い波)でパラメータを決めると, タイプIII(van der Pol型)が良い可能性がある 非線形パラメータとの相関 脳電位強度を示すパラメータB 脳電位変化率を示すパラメータA 今後の課題 調べたい脳波のタイプ (精神状態やてんかん脳波など) によって適切なモデルがある?
- 45. 终わり


![脳波とは神経細胞の活動電位
EEG: ElectroEncephaloGram
ECoG: ElectroCoticoGram
頭皮上電位
皮質上電位
二つの違いを比べる
EEG ECoG
取得コスト 低 高
侵襲性 無 有
信号明瞭さ 低 高
±10 ~ 100 μV
(noise)
-80 ~ +40 mV [1]
[1] 脳波の謎:リズムとその存在理由,良峯徳和,多摩大学研究紀要「経営情報研究」,No21 (2017) pp. 93-100.
減衰](https://image.slidesharecdn.com/labreporteeganalysis-181021053910/85/EEG-analysis-nonlinear-2-320.jpg)
![脳波とは神経細胞の活動電位
EEG: ElectroEncephaloGram
ECoG: ElectroCoticoGram
頭皮上電位
皮質上電位
二つの違いを比べる
EEG ECoG
取得コスト 低 高
侵襲性 無 有
信号明瞭さ 低 高
±10 ~ 100 μV
(noise)
-80 ~ +40 mV [1]
[1] 脳波の謎:リズムとその存在理由,良峯徳和,多摩大学研究紀要「経営情報研究」,No21 (2017) pp. 93-100.
EEG vs ECoG
どの分野でどのように利用したいかによって決まる
脳波 2 脳波
コミュニケーション
(カーツワイル)
エンタメ
感情推定Necomimi, Neurowear,
Japan, O?cial video
電脳世界
診断
BMI
スタンフォード大学による麻痺患者の応用例
Christine Lowe Having an Epileptic Seizure (Graphic)
減衰](https://image.slidesharecdn.com/labreporteeganalysis-181021053910/85/EEG-analysis-nonlinear-3-320.jpg)

![OUTPUT:個人差を考慮しないヒトの状態推定
脳波信号の処理 → 時間周波数解析(最強)
頭部14channelの計測可
(Emotiv EPOC+,
EMOTIV,
San Francisco, U.S.A )
周波数解析により状態区別が可能
ただ解析アルゴリズム(BlackBox)非公開なため研究者として気になる
各種状態が数値化されて
表示される
Necomimi, Neurowear, Japan, O?cial
video
[2] Time Frequency analysis of Olfactory induced EEG-power change, V. Alexander, et al., PLOS biomaterial,
https://doi.org/10.1371/journal.pone.0185596 (2017) pp.1-11.
[3] Toward an?EEG-based recognition of music liking using time-frequency?analysis,
SK Hadjidimitriou, IEEE Transaction on Biomedical, Vol. 52, Issue 12 (2012) pp. 3498 - 3510.
現状,特定の強い感覚刺激(匂い&音 and MORE)に対しては
時間周波数解析でも論文がアクセプトされている状況[2, 3].
周波数解析のみでいくのはレッドオーシャン(病理は除く)
コンシューマ用途では
ほぼ100%FFTが用いられる
7月に購入しました!](https://image.slidesharecdn.com/labreporteeganalysis-181021053910/85/EEG-analysis-nonlinear-5-320.jpg)
![OUTPUT:ブレインマシンインターフェース(BMI)の実装!?
脳波信号の処理 → 加算平均,独立成分分析
[4] Eog/Erp Hybrid Human-Machine Interface For Robot Control, Jiaxin Ma, Yu Zhang, Yunjun Nam, Andrzej Cichocki And
Fumitoshi Matsuno, Proc. Ieee/Rsj International Conference On Intelligent Robots And Systems (Iros2013), Pp.859-864, 2013.
Kyoto Univ., Matsuno Lab, Mechatronics
Lab. [4]
加算平均,独立成分分析,ERP(Event Relativ Potencial)
Sの視覚刺激に対して300 msec後に,
頭頂部でマイナス電位が見られる
Tの低頻度刺激では反射が遅れる
?特定の刺激を用意する必要がある
?装置が大掛かり.
?個人差によるためパーソナライズ
?もちろん感情は分からない
デメリットとERPの課題](https://image.slidesharecdn.com/labreporteeganalysis-181021053910/85/EEG-analysis-nonlinear-6-320.jpg)

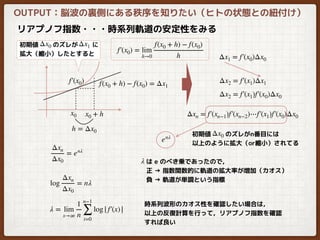
![OUTPUT:脳波の裏側にある秩序を知りたい(ヒトの状態との紐付け)
脳波信号の処理 → 非線形解析(リアプノフ指数,相関次元など)
脳波は非線形性(カオス性)が認められていて,線形解析では厳密に解けない
Δxn
Δx0
= enλ
λリアプノフ指数 ???
指数が正を返せば“カオス”
を含んでいるとされる.しか
しランダムノイズでも“正”を
返す場合もある
の軌道に対する の離れ度合いx0 xn
λ = lim
x→∞
1
n
n?1
∑
i=1
log| f′(x)|
リラックス脳波 100 sec
ストレス脳波 100sec
Sampling 0.002 sec
実験データは最近アクセプト
された論文のものを使用 [5]
解析窓 = 1秒間 500 sample
(1秒ごとのカオスを計測)
[5]上原賢祐,齊藤俊,”カオス性を持つヒト脳波の非線形ダイナミクスに着目した解析手法の提案”,
日本機械学会論文集,Vol.84, No.864 (2018.8), pp.18-00218.
集中時の脳波の方が,リアプノフ指数が全体的に大
きく,カオス的に振る舞うことが確認された
予測:
リラックス状態の方が,カオス度合いが大きいと
予測していたが,それとは異なる
単純に軌道安定性の観点から,波形が”カオス”と
いうものを示唆するだけで,カオス度合いは明確
には測れないのか?
アルファ波 [8 -13 Hz]](https://image.slidesharecdn.com/labreporteeganalysis-181021053910/85/EEG-analysis-nonlinear-9-320.jpg)
![OUTPUT:脳波の裏側にある秩序を知りたい(ヒトの状態との紐付け)
カオス解析???リアプノフ指数
文献調査や,脳波信号の対象による調査など細かいことを実施.
?他の研究者が類似の調査をしてないか?
?てんかんの状態ではどうか?
?脳波以外の生体信号ではどうか?
→ おおよそ10以下の正の値
→ 上昇する(5~8)
→ 指先脈波で正となる?
(脳波と同様)
Answer
てんかん脳波の場合
(ch1, ch2に注目)
指先脳波でも脳波と同様な値を観測[6]
[6]前田優輔,鈴木平,”問題解決における思考リズムの変容ーダイナミカルシステム?アプローチの観点からー”,桜美林大学心理学研究,
Vol.7 (2016), pp.117-130.
脳波解析の分野ではカオスの確認はこれで良しとされているものの,
未だ確定的に値の議論はされてなく,何かしらの参考材料程度で扱われている指標](https://image.slidesharecdn.com/labreporteeganalysis-181021053910/85/EEG-analysis-nonlinear-10-320.jpg)
![OUTPUT:脳波の裏側にある秩序を知りたい(ヒトの状態との紐付け)
脳波信号の処理 → 非線形解析(リアプノフ指数,相関次元など)
相関次元??時系列データに隠されたアトラクタ構造を取る次元をみる
x
v
x x
sin wave
時系列データの変位-速度の
プロットをして見ると何かしらの
状態が見てくるのでは
はたして,2次元空間でそれが記述できるのか?
3次元,4次元,???more
が必要ではないのか?
カオスの次元 = 非整数 [7]
[7]池口徹,山田泰司,小室元政,”カオス時系列の基礎と応用”,産業図書,(2002).
t](https://image.slidesharecdn.com/labreporteeganalysis-181021053910/85/EEG-analysis-nonlinear-11-320.jpg)
![OUTPUT:脳波の裏側にある秩序を知りたい(ヒトの状態との紐付け)
脳波信号の処理 → 非線形解析(リアプノフ指数,相関次元など)
相関次元 D2???時系列データに隠されたアトラクタをみる
[8]合原一幸,”ニューラルシステムにおけるカオス”,東京電気大学出版社,(1993).
相関次元のデータセットを作成 [8]
Xi
Xj = (x1, x2, ?xm)
Xj
Xj
r
データセットを
m次元空間にプロット
注目するベクトル と他ベクトル の距離XjXi
相関次元は,あるベクトルを中心に,その他周辺ベクトルが存在する確率piを単純に積分で解いたもの
?Xj |Xi|
pi =
1
N
N
∑
j=1
H(r ? |Xi ? Xj |) H(r ? |Xi ? Xj |) = 0, r < |Xi ? Xj |
H(r ? |Xi ? Xj |) = 1, r ≧ |Xi ? Xj |
確率
ヘビサイド関数
D2 = lim
r→0
log C(r)
log r
(C(r) ≡
N
∑
i=1
p2
i )
相関次元
m:次元
τ:時間遅れ](https://image.slidesharecdn.com/labreporteeganalysis-181021053910/85/EEG-analysis-nonlinear-12-320.jpg)
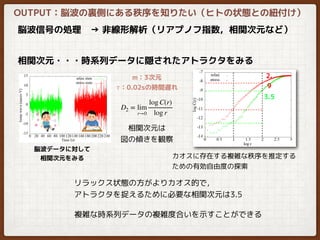
![相関次元の更なる探求
3.5次元で脳波のある秩序を記述することが可能か?
m次元の相関次元を導出
(左:リラックス 右:ストレス)
m: 3次元
τ: 0.02sの時間遅れ
例えば,埋め込み次元を変化させると…
ストレス時の方が
傾きが大きくなる
有効自由度が増す
m: 5次元
τ: 0.02s
相関次元の解決できていない問題
偽の相関次元値
?スケーリングの問題,総データ数
?傾きをどこで取るか定義が
はっきりしてない
?算出された有効次元を再度
図示する手法がない
ビッグデータを収集して,
まとめ上げるのが現在主流だったりする
[8]合原一幸,”ニューラルシステムにおけるカオス”,東京電気大学出版社,(1993).
これまで明らかにされている相関次元の例[8]](https://image.slidesharecdn.com/labreporteeganalysis-181021053910/85/EEG-analysis-nonlinear-14-320.jpg)
![OUTPUT:脳波の裏側にある秩序を知りたい(ヒトの状態との紐付け)
脳波信号の処理 → 非線形解析(リアプノフ指数,相関次元など)
<上記の具体的な諸問題>
?系全体の複雑性は観察できるが,実測波形の細かい変動を追わないので,
ヒトの精神的,生理的なもので変動する脳波の根本的な結びつけが困難である
相関次元
アトラクタ(時間発展の郡)の任意の点における半径 r と
その径内に含まれる他アトラクタの構成点を数える
カオスに存在する複雑な秩序を推定するための有
効自由度の探索
C(r) :相関積分
直線部の傾き値が
相関次元に対応する
m:埋め込み次元
(アトラクタ次元)
従来されている非線形(カオス)解析では,カオスの存在は確認する
ことは可能であるが,ヒトの状態を推定する目的では!?
Δxn
Δx0
= enλ
リアプノフ指数
指数が正を返せば“カオス”を含んでいるとされる
しかしランダムノイズでも“正”を返す場合もある
の軌道に対する の離れ度合いxnx0
D2 = lim
r→0
∑
N
i=1
C(r)
log r
[5]上原賢祐,齊藤俊,”カオス性を持つヒト脳波の非線形ダイナミクスに着目した解析手法の提案”,日本機械学会論文集,Vol.84, No.864 (2018.8), pp.18-00218.
λ = lim
x→∞
1
n
n?1
∑
i=1
log| f′(x)|](https://image.slidesharecdn.com/labreporteeganalysis-181021053910/85/EEG-analysis-nonlinear-15-320.jpg)

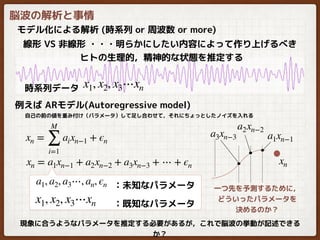
![モデル化による解析 (時系列 or 周波数 or more)
線形 VS 非線形 ???明らかにしたい内容によって作り上げるべき
ヒトの生理的,精神的な状態を推定する
脳波の解析と事情
2005
ARモデルがよく使われてた[9][10][11]
非線形モデルが主流
[10]西田茂人,他4名,”脳波モデルを用いた優位律動の特徴表現と背景脳波の自動判定”,生体医工学会,Vol.43, No.3 (2005), pp.447-455.
xn =
4
∑
i=1
aixn?1 sin(2πminΔt) + bi sin(2πminΔt) + ?n
脳波の振る舞いに特化したARモデル[10]
[9]深見忠典,他4名,”局所定常自己回帰モデルを用いた脳波特徴波検出”,電気学会論文誌,Vol.122, No.9 (2002), pp.1553-1559.
[11]Gelareh M.,et al,”Person Identi?cation by Using AR model for EEG Signal”,Proceedings of World Academy of Science and
Technology,Vol.11, ISSN 1307-6884 (2006), pp.281-285.
2010
線形 VS 非線形 論争[12][13]
非線形モデルの方が,
波形フィット率およびパラメータの意味づけの面で軍配
パラメータ同定の困難さの向上[12][13]
[12]Parham G.,et al,”Stochastic Dynamic Modeling of the Human Brain EEG Signal”,ASME 2013 Dynamic Systems and Control
Conference,Vol.2, No.DSCC2013-3881 (2013), pp.V002T22A003.
[13]上原賢祐,齊藤俊,”脳波信号を対象としたEPIAモデル構造に関する研究”,Dynamics and Design Conference 2018, No.18-7, 283 (2018.8)](https://image.slidesharecdn.com/labreporteeganalysis-181021053910/85/EEG-analysis-nonlinear-18-320.jpg)
![本研究の狙いと進捗について
ヒトの生理的,精神的状態を見るために
脳波の時系列データを如何にモデリングするか?
カオス性を有する脳波は不規則的な振る舞いをする
→ ある臨界時間以下であれば定量的な解析が可能?
··x + A ·x + Bx + Cx3
= P1cosωt + P2sinωt
線形項
非線形振動子:粘性減衰振動系 + Du?ng型の非線形項
非線形項 外部入力項
<モデリングの根拠>
?脳波の変動機序は決定論的カオスに従う
? 確率的要素を内包せずに,初期状態から未来の状態が一意に記述できる [14]
[14]Ben. H. Janson, “Quantitative analysis of electroencephalograms: is there chaos in the future?”, International journal of bio-medical computing,
No.95-123, (1991).
狙い:初期値(x0, v0)を与えて,ある解析窓ごとにモデルパラメータを
脳波変動に合うように同定すると状態推定が可能になる](https://image.slidesharecdn.com/labreporteeganalysis-181021053910/85/EEG-analysis-nonlinear-19-320.jpg)
![本研究の狙いと進捗について
ヒトの生理的,精神的状態を見るために
脳波の時系列データを如何にモデリングするか?
脳波の変動機序は決定論的カオスに従う[14]
?未来の状態が記述できる
?しかし,初期値によってt→∞の値が大きく異なる
··x + A ·x + Bx + Cx3
= P1cosωt + P2sinωt脳波の非線形振る舞いモデル
A = 13.0
B = 3994.0
C = 1297.0 ω = 61.0
初期位置 = 0.0
初期速度(紫) = 1.0
初期速度(緑) = 1.1
P1 = 800.0
P2 = 1500.0
0.1の初速の差で20秒後には
完全に波形が合わなくなる
今回のモデルが脳波に適している
と考えられる大きな理由の一つである
パラメータをある時間窓ごとに
実験的に同定していくことで
状態推定が可能では(EPIA)](https://image.slidesharecdn.com/labreporteeganalysis-181021053910/85/EEG-analysis-nonlinear-20-320.jpg)
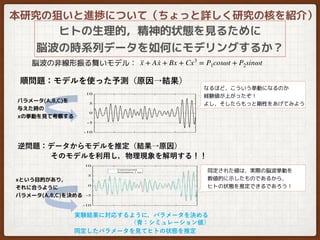
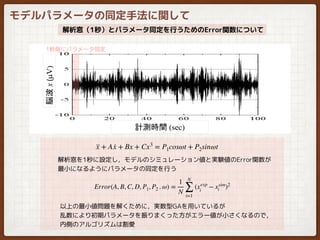
![リラックス VS ストレス脳波の検討
リラックス脳波 100 sec
ストレス脳波 100sec
Sampling 0.002 sec
解析窓 = 1秒間 500 sample
アルファ波 [8 -13 Hz]
リラックス
ストレス
リラックス,ストレス脳波ともに,
実測値の振る舞いに一致している
ことが分かる
ヒトの状態を推定
··x + A ·x + Bx + Cx3
= P1cosωt + P2sinωt](https://image.slidesharecdn.com/labreporteeganalysis-181021053910/85/EEG-analysis-nonlinear-23-320.jpg)
![リラックス VS ストレス脳波の検討
ヒトの状態推定を行うために各パラメータ値の調査
··x + A ·x + Bx + Cx3
= P1cosωt + P2sinωt
リラックス時とストレス時の違いを数値的にみる
平均値
?非線形パラメータ C が極端に低下 (30.2倍)
?線形パラメータのバネ定数 B は増加(1.37倍)
?線形パラメータのダンピング定数 A は微増(1.1倍)
? ?
集中状態になると
集中状態になると,これまでカオス的に活動していた脳活動が線形的になる [5]
しかしながら,この結果の解釈は容易であるが,従来のカオス解析とは異なる
[5]上原賢祐,齊藤俊,”カオス性を持つヒト脳波の非線形ダイナミクスに着目した解析手法の提案”,日本機械学会論文集,Vol.84, No.864 (2018.8), pp.18-00218.](https://image.slidesharecdn.com/labreporteeganalysis-181021053910/85/EEG-analysis-nonlinear-24-320.jpg)



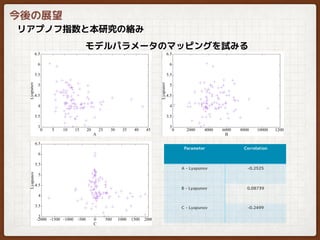
![パラメータ同定解析窓の延長 (2秒)[15]](https://image.slidesharecdn.com/labreporteeganalysis-181021053910/85/EEG-analysis-nonlinear-31-320.jpg)
![パラメータ同定解析窓の延長 (2秒)[15]
[15]上原賢祐,齊藤俊,”非線形振動子を用いた脳波モデルの精度検証”,日本機械学会関西支部92期定時総会講演会,M416 ,No.174-1 (2017.3).](https://image.slidesharecdn.com/labreporteeganalysis-181021053910/85/EEG-analysis-nonlinear-32-320.jpg)
![パラメータ同定解析窓の延長 (2秒)[15]
[15]上原賢祐,齊藤俊,”非線形振動子を用いた脳波モデルの精度検証”,日本機械学会関西支部92期定時総会講演会,M416 ,No.174-1 (2017.3).](https://image.slidesharecdn.com/labreporteeganalysis-181021053910/85/EEG-analysis-nonlinear-33-320.jpg)
![パラメータ同定解析窓の延長 (2秒)[15]
[15]上原賢祐,齊藤俊,”非線形振動子を用いた脳波モデルの精度検証”,日本機械学会関西支部92期定時総会講演会,M416 ,No.174-1 (2017.3).](https://image.slidesharecdn.com/labreporteeganalysis-181021053910/85/EEG-analysis-nonlinear-34-320.jpg)