Elect principles -_ac_waveform_year1
- 1. AC Wavefrom – The AC Waveform The waveform of an alternating current generally follows the sine function and is known as ‘sinusoidal’. It is stated as being alternating because it changes polarity every half-cycle. -1.50 -1.00 -0.50 0.00 0.50 1.00 1.50 0 20 40 60 80 100 120 140 160 180 200 220 240 260 280 300 320 340 360 Peak-to-Peak Peakvalue 1 cycle Ø degrees
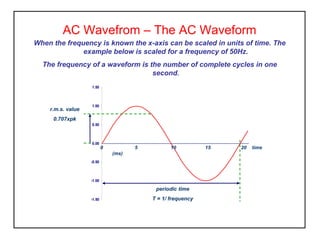
- 2. -1.50 -1.00 -0.50 0.00 0.50 1.00 1.50 r.m.s. value 0.707xpk 0 5 10 15 20 time (ms) periodic time T = 1/ frequency AC Wavefrom – The AC Waveform When the frequency is known the x-axis can be scaled in units of time. The example below is scaled for a frequency of 50Hz. The frequency of a waveform is the number of complete cycles in one second.
- 3. AC Waveform – The AC Waveform A circle is usually expressed in terms of degrees however when working with electrical waveforms it is more common to use the Radian. 0° or 2π radian180° or π radian 2 90° or π radian 2 270° or 3π radian ω rad/s Angular Velocity
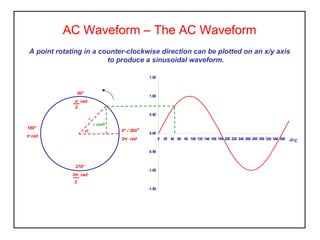
- 4. AC Waveform – The AC Waveform A point rotating in a counter-clockwise direction can be plotted on an x/y axis to produce a sinusoidal waveform. -1.50 -1.00 -0.50 0.00 0.50 1.00 1.50 0 20 40 60 80 100 120 140 160 180 200 220 240 260 280 300 320 340 360 deg 0° / 360° 2π rad 180° π rad 2 90° π rad 2 270° 3π rad Ø r r sinØ