Modular Design Principles for Quantum Devices
Download as PPTX, PDF
0 likes388 views
This document discusses a project to apply modular design principles to quantum computing devices. The goals are to identify how modular design can reduce errors and improve control of quantum operations. Initial results show modularity allows for improved control of qubit operations. The project aims to revolutionize quantum computing by establishing modular design as an approach to develop quantum algorithms and benefit from increased freedom for designers.
Modular Design Principles for Quantum Devices
- 1. Modular Design Principles for Quantum Devices PI Elica Kyoseva International Design Center
- 2. Quantum computers New Scientist, October 2013 Quantum computers process information in quantum bits, or qubits, which can be both 0 and 1 at the same time. This allows quantum chips to vastly outperform regular PCs. The applications are vast! Our mission Apply a very well established principle of design science modular design to revolutionize the current state of quantum computing devices Identify the degree of module freedom available to designers of quantum computation algorithms and the anticipated benefits of applying modular design approach
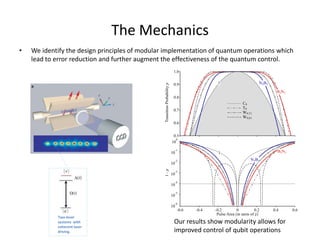
- 3. The Mechanics We identify the design principles of modular implementation of quantum operations which lead to error reduction and further augment the effectiveness of the quantum control. Transition Probability p 1.0 1 0.9 N3B3 B3N3 0.8 C9 T9 W9,T1 W9,S1 0.7 0.6 0.5 0 10 10 10 1-p 10 10 10 10 -1 N3B3 -2 -3 -4 -5 -6 -0.6 Two-level systems with coherent laser driving. B3N3 1 -0.4 -0.2 0 0.2 Pulse Area (in units of p) 0.4 Our results show modularity allows for improved control of qubit operations 0.6