�ݺ�ߣ

SPH4C Unit #3 – Energy Transformations
Law of Conservation of Energy

Learning Goals and Success Criteria
Today I will be able to…
• Define the Law of Conservation of Energy and
how it applies to energy changes,
• Describe how energy transformation occur
between its different forms given a scenario,
• Use the Law of Conservation of Energy to solve
related problems

Mechanical Energy
Objects may possess kinetic energy
only, gravitational potential energy
only or a combination of both
(mechanical energy). For example:
• A hockey puck sliding on the flat
ice has kinetic energy only
• An acorn hanging in a tree has
gravitational potential energy
only
• A parachutist falling has both
kinetic and gravitational
potential energy

Types of Energy
Mechanical Energy
• Sum of an object’s kinetic
and gravitational potential
energy
𝐸𝑚𝑒𝑐ℎ𝑎𝑛𝑖𝑐𝑎𝑙 = 𝐸𝑘 + 𝐸𝑔

Energy Transformations
If you recall, there are many types of energy in the universe and the
conservation of energy from one form to another is called an energy
transformation. For example, in a microwave oven, electrical energy
transforms into radiant energy (microwaves), which is then transformed into
thermal energy in the food being cooked.
Electrical energy  radiant energy  thermal energy
Energy Transformation
The change of energy from one form to another.

Energy Transformations
People often wonder how much energy there is in the universe and whether
we will eventually run out of energy. Scientists have studied energy and
energy transformations and have arrived at some important generalizations.
For example, they noticed that when one form of energy is transformed into
another form (or forms) of energy, the quantity of one form is reduced by the
same amount that the quantity of the other form (or forms) is increased. For
example, a light bulb may transform 100 J of electrical energy into 5 J of
radiant energy and 95 J of thermal energy. However, the total amount of
energy has not changed.
= +
100 J
of electrical energy
95 J
of thermal energy
5 J
of radiant energy

This generalization, known as the law of conservation of energy, is stated as
follows:
The total amount of energy in the universe is conserved. There is a certain
total amount of energy in the universe, and this total never changes. New
energy cannot be created out of nothing, and existing energy cannot
disappear; the energy that exists can only be changed from one form into
another. When an energy transformation occurs, no energy is lost.

Energy is neither created or destroyed, it can only change from one form to
another. When energy changes from one form to another, no energy is lost.
Note:
Evidence of the law of conservation of energy is all around us, but to notice it,
you need to take measurements and perform simple calculations. Consider a
65.0 kg diver who performs a handstand dive from a 10.0 m high diving
platform into the water below…
Etotal @ start = Etotal during = Etotal @ end

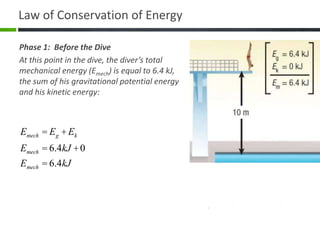
Phase 1: Before the Dive
The diver begins the dive in a handstand
position on the platform of the diving tower.
Since he is motionless, the diver’s kinetic
energy is equal to zero (Ek = 0), and his
gravitational potential energy is calculated as
follows:
Eg = mgh
Eg = (65.0kg)(9.8N / kg)(10.0m)
Eg = 6370 J or 6.4 kJ

Phase 1: Before the Dive
At this point in the dive, the diver’s total
mechanical energy (Emech) is equal to 6.4 kJ,
the sum of his gravitational potential energy
and his kinetic energy:
Emech = Eg + Ek
Emech = 6.4kJ + 0
Emech = 6.4kJ

Phase 2: At the Halfway Point
At the halfway point, the diver is 5.0 m above
the water’s surface (and is still accelerating
at 9.8 m/s2 towards the water). At this point
in the dive, the diver’s gravitational potential
may be calculated as follows:
Eg = mgh
Eg = (65.0kg)(9.8N / kg)(5.0m)
Eg = 3185 J or 3.2 kJ

At the halfway point, the diver’s kinetic
energy may be calculated as well. But first,
his velocity at the halfway point must be
calculated:
vf
2
= vi
2
+ 2aDd where vi = 0
vf = 2(9.8m / s2
)(5.0m)
vf = 9.899 m / s
Ek =
1
2
mv2
Ek =
1
2
(65.0kg)(9.899m / s)2
Ek = 3185 J or 3.2 kJ

At the halfway point, the diver’s total
mechanical energy is still 6.4 kJ, the sum of
his gravitational potential energy and his
kinetic energy:
Emech = Eg + Ek
Emech = 3.2kJ +3.2kJ
Emech = 6.4kJ

Phase 3: At the Water’s Surface
When the diver reaches the surface of the
water, his height above the water is 0 m and
so his gravitational potential energy is equal
to zero (Eg = 0). His kinetic energy is
calculated as follows:
vf
2
= vi
2
+ 2aDd where vi = 0
vf = 2(9.8m / s2
)(10.0m)
vf =14.0 m / s
Ek =
1
2
mv2
Ek =
1
2
(65.0kg)(14.0m / s)2
Ek = 6370 J or 6.4 kJ

Phase 3: At the Water’s Surface
At the water’s surface, the diver’s total
mechanical energy is still 6.4 kJ, the sum of
his gravitational potential energy and his
kinetic energy:
Emech = Eg + Ek
Emech = 0+6.4kJ
Emech = 6.4kJ

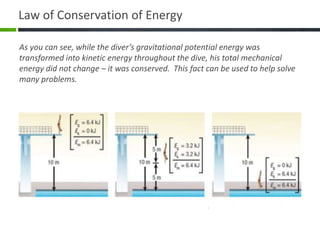
As you can see, while the diver’s gravitational potential energy was
transformed into kinetic energy throughout the dive, his total mechanical
energy did not change – it was conserved. This fact can be used to help solve
many problems.

Practice
1. A ball is dropped vertically from a height of 1.5 m; it bounces back to a
height of 1.3 m. Does this violate the law of conservation of energy?
Explain.
No, it does not violate the law of conservation of energy. This is because
some of the kinetic/elastic energy was transformed into other forms of
energy such as sound/frictional. As a result, less energy was available to be
transformed back into kinetic energy and thus gravitational potential energy.

Practice
2. A 56 kg diver jumps off the end of a 7.5 m platform
with an initial horizontal speed of 3.6 m/s.
a) Determine the diver’s total mechanical energy
at the end of the platform relative to the
surface of the water below.

Practice
b) Apply the law of conservation of energy to
determine the diver’s speed at a height of 2.8 m
above the water.

Practice
c) Repeat (b) to find the maximum speed of the
diver upon reaching the water.

Practice
3. A 0.20 kg ball is thrown straight up from the edge of a 30.0 m tall building
at a velocity of 22.0 m/s. The ball moves up to the maximum height and
then falls to the ground at the base of the building. Use the law of
conservation of energy to answer the following questions, assuming that
the reference level for gravitational potential energy is ground level.
a) What is the total energy of the ball at the start when it had a velocity
of 22.0 m/s?

Practice
b) What is the velocity of the ball at the maximum height?

Practice
c) What is the maximum height of the ball?

Practice
d) What is the velocity of the ball when it hits the ground?

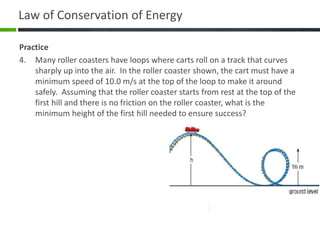
Practice
4. Many roller coasters have loops where carts roll on a track that curves
sharply up into the air. In the roller coaster shown, the cart must have a
minimum speed of 10.0 m/s at the top of the loop to make it around
safely. Assuming that the roller coaster starts from rest at the top of the
first hill and there is no friction on the roller coaster, what is the
minimum height of the first hill needed to ensure success?

Homework
Read: Pg. 152-153
Practice Problems: Pg. 153 #12

�ݺ�ߣ

Energy Conservation / Types of Potential Energy

More Related Content

Energy Conservation / Types of Potential Energy

Editor's Notes