Energy Efficient Compression of Shock Data using Compressed Sensing
- 1. Energy Ef’¼ücient Compression of Shock Data using Compressed Sensing Jerrin Thomas Panachakel, Finitha K.C., September 2, 2016
- 2. Overview Jerrin Thomas Panachakel jp@ee.iisc.ernet.in 2
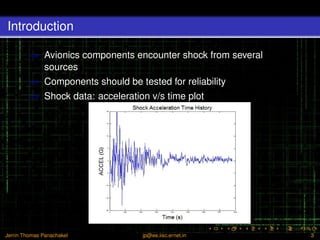
- 3. Introduction ŌćÆ Avionics components encounter shock from several sources ŌćÆ Components should be tested for reliability ŌćÆ Shock data: acceleration v/s time plot Jerrin Thomas Panachakel jp@ee.iisc.ernet.in 3
- 4. Problem ŌĆó Compression of Shock Data ŌĆó Constraints ŌĆó Computational complexity should be low ŌĆó Error should be minimum ŌĆó Why CS? ŌĆó Shock data is sparse in multiple domains ŌĆó Has lower computational complexity ŌĆó Has almost equal compression ef’¼üciency Jerrin Thomas Panachakel jp@ee.iisc.ernet.in 4
- 5. Shock Data (1/2) ŌĆó Plot of magnitude of shock pulses v/s time ŌĆó Causes1: ŌĆó Rocket motor ignition ŌĆó Staging events ŌĆó Deployment events ŌĆó Measured using accelerometers 1Tom Irvine. ŌĆ£An Introduction to the Vibration Response SpectrumŌĆØ. In: Rev C, Vibrationdata (2000). Jerrin Thomas Panachakel jp@ee.iisc.ernet.in 5
- 6. Shock Data (2/2) source: https://www.youtube.com/watch?v=KZVgKu6v808 Jerrin Thomas Panachakel jp@ee.iisc.ernet.in 6
- 7. Shock Respose Spectra ŌĆó Calculated from acceleration time history ŌĆó For estimating damage potential ŌĆó For estimating integrity of shock data Figure: SRS Jerrin Thomas Panachakel jp@ee.iisc.ernet.in 7
- 8. Shock Respose Spectra- Calculation (1/2) Figure: SRS Model Žēni = Ki Mi (1) Jerrin Thomas Panachakel jp@ee.iisc.ernet.in 8
- 9. Shock Respose Spectra- Calculation (2/2) (a) Shock data and response to SDOF systems (b) Shock data and Shock Response Spectra data Figure: Shock data and SRS Jerrin Thomas Panachakel jp@ee.iisc.ernet.in 9
- 10. Integrity from SRS (a) SRS of a saturated shock data (b) SRS of a good shock dataJerrin Thomas Panachakel jp@ee.iisc.ernet.in 10
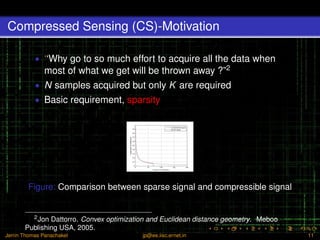
- 11. Compressed Sensing (CS)-Motivation ŌĆó ŌĆśŌĆśWhy go to so much effort to acquire all the data when most of what we get will be thrown away ?ŌĆØ2 ŌĆó N samples acquired but only K are required ŌĆó Basic requirement, sparsity Figure: Comparison between sparse signal and compressible signal 2Jon Dattorro. Convex optimization and Euclidean distance geometry. Meboo Publishing USA, 2005. Jerrin Thomas Panachakel jp@ee.iisc.ernet.in 11
- 12. Mathematics behind CS (1/3) x = N i=1 siŽłi (2) weighing coef’¼ücients, si =< x, ╬© >, x Ōłł RN or equivalently, x = ╬©s (3) y = ╬”x (4) using (3), y = ╬”╬©s = ╬śs (5) Jerrin Thomas Panachakel jp@ee.iisc.ernet.in 12
- 13. Mathematics behind CS (2/3) ŌĆó Recoverable if the four columns are LI ŌĆó For M measurements, all M ├Ś K sub-matrices are ideally close to orthonormal basis ŌĆó RIP: 1 ŌłÆ Ōēż ||╬”v||2 ||v||2 Ōēż 1 + Jerrin Thomas Panachakel jp@ee.iisc.ernet.in 13
- 14. Mathematics behind CS (3/3) ŌĆó Design of RIP matrix is almost impossible ŌĆó RIP matrices are around us!3 ŌĆó iid Gaussian ŌĆó iid Bernoulli ŌĆó M Ōēź cKlog(N K ) Figure: Gerhard Richer- 4096 Farben 3Jerrin Thomas Panachakel jp@ee.iisc.ernet.in 14
- 15. Recovery (1/3) ŌĆó Solution to ╬”s = y lies in the translated null space of ╬ś ŌĆó 2 recovery: ŌĆó ╦åS = argmin||s ||2, such that ╬śS = y Figure: 2 minimization Jerrin Thomas Panachakel jp@ee.iisc.ernet.in 15
- 16. Recovery (2/3) ŌĆó 0 recovery: ŌĆó ╦åS = argmin||s ||0, such that ╬śS = y ŌĆó Computationally complex ŌĆó 1 recovery: ŌĆó ╦åS = argmin||s ||1, such that ╬śS = y Figure: 1 minimization Jerrin Thomas Panachakel jp@ee.iisc.ernet.in 16
- 17. Recovery (3/3) Figure: Sparse signal and its reconstruction Jerrin Thomas Panachakel jp@ee.iisc.ernet.in 17
- 18. Sparsity Analysis (a) Time (b) DCT (c) Haar (d) Daubechies Jerrin Thomas Panachakel jp@ee.iisc.ernet.in 18
- 19. Performance Metrics ŌĆó Percentage Root Mean Square Difference: [1] PRD = N n=1 (x[n] ŌłÆ ╦åx[n])2 N n=1 (x[n] ŌłÆ ┬»x[n])2 ├Ś 100% (6) ŌĆó Compression Ratio: [1] CR = Norg ŌłÆ Ncomp Norg ├Ś 100 (7) ŌĆó Execution time Jerrin Thomas Panachakel jp@ee.iisc.ernet.in 19
- 20. Time Domain (a) (b) (c) Jerrin Thomas Panachakel jp@ee.iisc.ernet.in 20
- 21. Shock Respnse Spectra (a) (b) (c) Jerrin Thomas Panachakel jp@ee.iisc.ernet.in 21
- 22. PRD v/s CR Figure: PRD v/s CR Jerrin Thomas Panachakel jp@ee.iisc.ernet.in 22
- 23. Time v/s CR Figure: Execution Time v/s CR Jerrin Thomas Panachakel jp@ee.iisc.ernet.in 23
- 24. Conclusion ŌĆó Shock data compression performed using CS ŌĆó CS inferior in terms of PRD for higher CR ŌĆó CS is almost 1000 times faster than thresholding based DWT compression ŌĆó Implemented technique satis’¼ües the requirements Jerrin Thomas Panachakel jp@ee.iisc.ernet.in 24
- 25. Jerrin Thomas Panachakel jp@ee.iisc.ernet.in 25

















![Performance Metrics
ŌĆó Percentage Root Mean Square Difference: [1]
PRD =
N
n=1
(x[n] ŌłÆ ╦åx[n])2
N
n=1
(x[n] ŌłÆ ┬»x[n])2
├Ś 100% (6)
ŌĆó Compression Ratio: [1]
CR =
Norg ŌłÆ Ncomp
Norg
├Ś 100 (7)
ŌĆó Execution time
Jerrin Thomas Panachakel jp@ee.iisc.ernet.in 19](https://image.slidesharecdn.com/pres3-170219063710/85/Energy-Efficient-Compression-of-Shock-Data-using-Compressed-Sensing-19-320.jpg)





