Equations in sc motion 2012
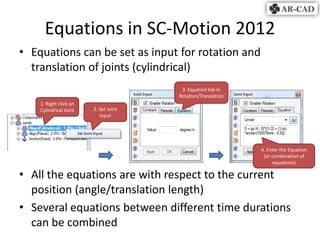
- 1. Equations in SC-Motion 2012 ŌĆó Equations can be set as input for rotation and translation of joints (cylindrical) 3. Equation tab in Rotation/Translation 1. Right click on Cylindrical Joint 2. Set Joint Input 4. Enter the Equation (or combination of equations) ŌĆó All the equations are with respect to the current position (angle/translation length) ŌĆó Several equations between different time durations can be combined
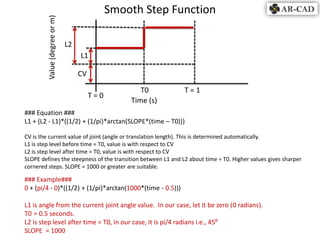
- 2. Smooth Step Function Value (degree or m) L2 L1 CV T0 T=1 T=0 Time (s) ### Equation ### L1 + (L2 - L1)*((1/2) + (1/pi)*arctan(SLOPE*(time ŌĆō T0))) CV is the current value of joint (angle or translation length). This is determined automatically. L1 is step level before time = T0, value is with respect to CV L2 is step level after time = T0, value is with respect to CV SLOPE defines the steepness of the transition between L1 and L2 about time = T0. Higher values gives sharper cornered steps. SLOPE = 1000 or greater are suitable. ### Example### 0 + (pi/4 - 0)*((1/2) + (1/pi)*arctan(1000*(time - 0.5))) L1 is angle from the current joint angle value. In our case, let it be zero (0 radians). T0 = 0.5 seconds. L2 is step level after time = T0, in our case, it is pi/4 radians i.e., 45Ōü░ SLOPE = 1000
- 3. Smooth Square Impulse Value (degree or m) H CV T1 T2 T=1 T=0 Time (s) ### Equation ### (H/pi)*(arctan(SLOPE*(time - T1)) - arctan(SLOPE*(time - T2))) CV is the current value of joint (angle or translation length). This is determined automatically. T1 is the start of the impulse. T2 is the end of the impulse. H is the height of the impulse, value is with respect to CV SLOPE defines the steepness of the transition between 0 and H about time = T1 and T2. Higher values gives sharper cornered impulses. SLOPE = 1000 or greater are suitable. ### Example### ((pi/4)/pi)*(arctan(1000*(time - 0.25)) - arctan(1000*(time - 0.75))) H = pi/4 (values should be in radians) T1 is the start of the impulse = 0.25 seconds T2 is the end of the impulse = 0.75 seconds SLOPE = 1000
- 4. Smooth Ramp Top Impulse Value (degree or m) H2 H1 CV T1 T2 T=1 T=0 Time (s) ### Equation ### ((1/pi)*(arctan(SLOPE*(time - T1)) - arctan(SLOPE*(time - T2))))*(((H2 - H1)/(T2 - T1))*(time - T1) + H1) This is similar to the square impulse but the top has a sloping ramp. It is good for building a smooth piecewise linear function by adding a series of these. CV is the current value of joint (angle or translation length). This is determined automatically. T1 is the start of the impulse. T2 is the end of the impulse. H1 is the height at T1 at the beginning of the ramp, value is with respect to CV. H2 is the height at T2 at the end of the ramp, value is with respect to CV. SLOPE defines the steepness of the transition between 0 and H1 and H2 to 0 about time = T1 and T2 respectively. Higher values gives sharper cornered impulses. SLOPE = 1000 or greater are suitable. ### Example### ((1/pi)*(arctan(1000*(time - 0.25)) - arctan(1000*(time - 0.75))))*((((pi/2)- (pi/4))/(0.75 - 0.25))*(time - 0.25) + (pi/4)) H1 = pi/4 (values should be in radians) ; H2 = pi/2 (values should be in radians) T1 is the start of the impulse = 0.25 seconds T2 is the end of the impulse = 0.75 seconds SLOPE = 1000
- 5. Combination of Equations Value (degree or m) H* CV R1 R2 R3 T1 T2 T=1 T=0 Time (s) This is a combination of R1 = Region 1: Smooth Ramp Top Impulse with H1 = 0; H2 = H*; Duration between T=0 and T1 R2 = Region 2: Smooth Square Impulse with H = H*; Duration between T1 and T2 R3 = Region 3: Smooth Ramp Top Impulse with H1 = H*; H2 = 0; Duration between T2 and T=1 ### Example Equation### ((1/pi)*(arctan(1000*(time - 0)) - arctan(1000*(time - 0.25))))*((((pi/4) - 0)/(0.25 - 0))*(time - 0) + 0) + ((pi/4)/pi)*(arctan(1000*(time - 0.25)) - arctan(1000*(time - 0.75))) + ((1/pi)*(arctan(1000*(time - 0.75)) - arctan(1000*(time - 1))))*(((0 - (pi/4))/(1 - 0.75))*(time - 0.75) + (pi/4)) H* = pi/4 (values should be in radians) ; T1 is the start of the impulse = 0.25 seconds T2 is the end of the impulse = 0.75 seconds Total duration is between 0 and 1 seconds SLOPE = 1000
- 6. Set Different Joint Value at end of Simulation Time Value (degree or m) H** H* CV R1 R2 R3 R4 T1 T2 T=1 T = 1000 T=0 Time (s) This is a combination of R1 = Region 1: Smooth Ramp Top Impulse with H1 = 0; H2 = H*; Duration between T=0 and T1 R2 = Region 2: Smooth Square Impulse with H = H*; Duration between T1 and T2 R3 = Region 3: Smooth Ramp Top Impulse with H1 = H*; H2 = H**; Duration between T2 and T=1 R4 = Region 4: Smooth Square Impulse with H = H**; Duration between T=1 and T=1000 (high value, instead of infinity) ### Example Equation### ((1/pi)*(arctan(1000*(time - 0)) - arctan(1000*(time - 0.25))))*((((pi/4) - 0)/(0.25 - 0))*(time - 0) + 0) + ((pi/4)/pi)*(arctan(1000*(time - 0.25)) - arctan(1000*(time - 0.75))) + ((1/pi)*(arctan(1000*(time - 0.75)) - arctan(1000*(time - 1))))*((((pi/2) - (pi/4))/(1 - 0.75))*(time - 0.75) + (pi/4)) + ((pi/2)/pi)*(arctan(1000*(time - 1)) - arctan(1000*(time - 1000))) H* = pi/4 (values should be in radians) ; H** = pi/2 (values should be in radians) T1 is the start of the impulse = 0.25 seconds; T2 is the end of the impulse = 0.75 seconds Total duration is between 0 and 1 seconds; SLOPE = 1000 We use a very high value of T= 1000 for a time that should not be reached
- 7. Value (degree or m) Joint 1 Sequential Joint Inputs: Joint 1 and Joint 2 H* Joint 1 moves between time CV R2 duration of R1 T=0 seconds and T1 T=1 T = 1000 T=T1. T=0 Time (s) R1 = Smooth Ramp Top Impulse; Between T=0 and T1;R2 = Smooth Square Impulse; Between T1 and T = 1000 (we want the value to be H* (with respect to CV) at T=1 ((1/pi)*(arctan(1000*(time - 0)) - arctan(1000*(time - 0.5))))*((((pi/2) - 0)/(0.5 - 0))*(time - 0) + 0) + ((pi/2)/pi)*(arctan(1000*(time - 0.5)) - arctan(1000*(time - 1000))) Value (degree or m) Joint 2 moves H** between time Joint 2 duration CV R1 R2 T=T1 and T=1 seconds. T1 T=1 T = 1000 T=0 Time (s) R1 = Smooth Ramp Top Impulse; Between T1 and T = 1 ; R2 = Smooth Square Impulse; Between T=1 and T = 1000 ; (we want the value to be H** (with respect to CV) at T=1 ((1/pi)*(arctan(1000*(time - 0.5)) - arctan(1000*(time - 1))))*((((pi/2) - 0)/(1 - 0.5))*(time - 0.5) + 0) + ((pi/2)/pi)*(arctan(1000*(time - 1)) - arctan(1000*(time - 1000)))