Euler graph
Download as PPTX, PDF3 likes5,931 views
The document discusses graphs and Eulerian circuits and paths. It defines what a graph is composed of and defines an Eulerian circuit and path. It states that a graph must be connected and have all vertices visited once for an Eulerian circuit, or have two odd vertices for an Eulerian path. Fleury's algorithm is described for finding an Euler circuit or path by traversing edges without crossing bridges twice. The algorithm works by choosing the next edge such that bridges are only crossed if necessary. Examples are given to demonstrate the algorithm. Applications mentioned include the Chinese postman problem and communicating networks.
1 of 22
Downloaded 82 times







![Fleury’s Algorithm
• Let G be an Eulerian graph.
• STEP 1: Choose any vertex v of G and set current vertex equal to v and
current trail equal to the empty sequence of edges.
• STEP 2: Select any edge e incident with the current vertex but choosing a
bridge only if there is no alternative.
• STEP 3: Add e to the current trail and set the current vertex equal to the
vertex at the ‘other end’ of e. [If e is a loop, the current vertex will not
move.]
• STEP 4: Delete e from the graph. Delete any isolated vertices.
• Repeat steps 2 – 4 until all edges have been deleted from G. The final
current trail is an Eulerian trail in G.](https://image.slidesharecdn.com/eulergraph-171129112603/85/Euler-graph-12-320.jpg)




Recommended
∫›∫›fl£s Chapter10.1 10.2



∫›∫›fl£s Chapter10.1 10.2showslidedump
Ã˝
This section provides an introduction to graphs and graph theory. Key points include:
- Graphs consist of vertices and edges that connect the vertices. They can be directed or undirected.
- Common terminology is introduced, such as adjacent vertices, neighborhoods, degrees of vertices, and handshaking theorem.
- Different types of graphs are discussed, including multigraphs, pseudographs, and directed graphs.
- Examples of graph models are given for computer networks, social networks, information networks, transportation networks, and software design. Graphs can be used to model many real-world systems and applications.Graph Theory



Graph TheoryEhsan Hamzei
Ã˝
This document provides an overview of graph theory, including its history and key concepts. It defines a graph as a set of nodes connected by edges. Important early contributors are noted, such as Euler's work on the Seven Bridges of Königsberg problem. Exact definitions of graph types like simple, directed, and weighted graphs are given. Key graph concepts explained in less than three sentences include connectivity, degree, paths, cycles, and trees. The document also briefly discusses representing graphs through adjacency lists and matrices. It concludes by thanking the reader and listing references.Graph theory Eulerian graph



Graph theory Eulerian graphrajeshree nanaware
Ã˝
This document discusses graph theory and the Eulerian graph and Chinese Postman problems. It begins by describing the Seven Bridges of Konigsberg problem and how it can be represented by a graph. It then defines an Eulerian graph as a connected graph where every vertex has an even degree, allowing an Eulerian circuit that uses each edge once. The Chinese Postman problem is described as finding the shortest route to traverse all edges of a graph that may not be Eulerian by pairing odd degree vertices. An algorithm is provided to solve the Chinese Postman problem through modifying the graph and finding an Euler circuit. An example graph is used to illustrate the process.Graph Theory: Trees



Graph Theory: TreesAshikur Rahman
Ã˝
The document discusses properties and theorems related to trees in graph theory. Some key points include:
- A tree is a connected acyclic graph with n vertices that has n-1 edges.
- There is a one-to-one correspondence between labeled trees with n vertices and sequences of n-2 labels, as proven by Cayley's theorem.
- Every connected graph has at least one spanning tree, which is a subgraph that contains all vertices. Fundamental circuits are formed when a chord is added to a spanning tree.
- Cyclic interchange can be used to generate all possible spanning trees by adding and removing edges.Euler paths and circuits



Euler paths and circuits03446940736
Ã˝
complete guide and training to what is Euler path and circuits with animations and examples
try it to believe it.
made by Shahbaadshah. Dijkstra's algorithm presentation



Dijkstra's algorithm presentationSubid Biswas
Ã˝
The solution to the single-source shortest-path tree problem in graph theory. This slide was prepared for Design and Analysis of Algorithm Lab for B.Tech CSE 2nd Year 4th Semester.
Introduction to Graph Theory



Introduction to Graph TheoryPremsankar Chakkingal
Ã˝
The document provides an introduction to graph theory. It begins with a brief history, noting that graph theory originated from Euler's work on the Konigsberg bridges problem in 1735. It then discusses basic concepts such as graphs being collections of nodes and edges, different types of graphs like directed and undirected graphs. Key graph theory terms are defined such as vertices, edges, degree, walks, paths, cycles and shortest paths. Different graph representations like the adjacency matrix, incidence matrix and adjacency lists are also introduced. The document is intended to provide an overview of fundamental graph theory concepts.introduction to graph theory



introduction to graph theoryChuckie Balbuena
Ã˝
This document provides definitions and theorems related to graph theory. It begins with definitions of simple graphs, vertices, edges, degree, and the handshaking lemma. It then covers definitions and properties of paths, cycles, adjacency matrices, connectedness, Euler paths and circuits. The document also discusses Hamilton paths, planar graphs, trees, and other special types of graphs like complete graphs and bipartite graphs. It provides examples and proofs of many graph theory concepts and results.Graph isomorphism



Graph isomorphismCore Condor
Ã˝
Graph isomorphism is the problem of determining whether two graphs are topologically identical. It is in NP but not known to be NP-complete. The refinement heuristic iteratively partitions vertices into equivalence classes to reduce possible mappings between graphs. For trees, there is a linear-time algorithm that labels vertices based on subtree structure to test rooted and unrooted tree isomorphism.Graph theory 



Graph theory iranian translate
Ã˝
This document provides an overview of graph theory and some of its common algorithms. It discusses the history of graph theory and its applications in various fields like engineering. It defines basic graph terminology like nodes, edges, walks, paths and cycles. It also explains popular graph algorithms like Dijkstra's algorithm for finding shortest paths, Kruskal's and Prim's algorithms for finding minimum spanning trees, and graph partitioning algorithms. It provides pseudocode, examples and analysis of the time complexity for these algorithms.Real life application



Real life applicationumadeviR3
Ã˝
Graph theory is the study of points and lines, and concepts like vertices and edges. It has many applications, including map coloring, Google Maps, and football games. Graph theory can be used to color maps with the minimum number of colors without any adjacent regions sharing the same color. It is also used in Google Maps for functions like estimating travel times and showing traffic conditions. In football, a match can be represented as a network with players as vertices and passes as edges, allowing analysis of things like which team has a more balanced network.Dijkstra's algorithm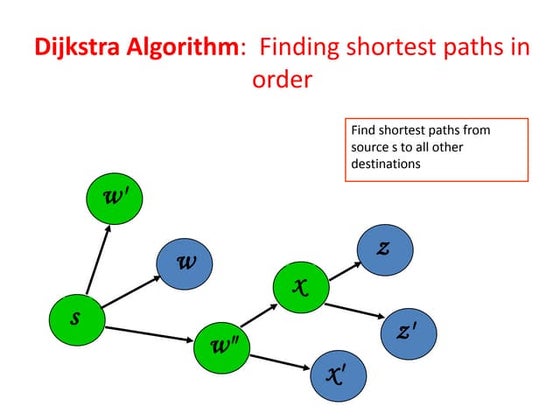



Dijkstra's algorithmgsp1294
Ã˝
Dijkstra's algorithm finds the shortest paths from a source node to all other nodes in a graph. It works by maintaining two sets - one for nodes whose shortest paths are determined, and one for remaining nodes. It iteratively selects the node with the smallest distance from the source, calculates the distances to its neighbors, and moves them to the determined set until all nodes are processed. Some applications include finding fastest routes in transportation networks like road maps or flight schedules.Applications of graphs



Applications of graphsTech_MX
Ã˝
Graph theory has many applications including social networks, data organization, and communication networks. The document discusses Dijkstra's algorithm for finding the shortest path between nodes in a graph and its application to finding shortest routes between cities. It also discusses using graph representations for fingerprint classification, where fingerprints are modeled as graphs with nodes for fingerprint regions and edges between adjacent regions. Fingerprints are classified based on the structure of these graphs and compared to model graphs for matching.Kruskal Algorithm



Kruskal AlgorithmBhavik Vashi
Ã˝
Kruskal's algorithm is a minimum spanning tree algorithm that finds the minimum cost collection of edges that connect all vertices in a connected, undirected graph. It works by sorting the edges by weight and then sequentially adding the shortest edge that does not create a cycle. The algorithm uses a disjoint set data structure to track connected components in the graph. It runs in O(ElogE) time, where E is the number of edges.Introduction to Graph Theory



Introduction to Graph TheoryYosuke Mizutani
Ã˝
This document introduces the topic of graph theory. It defines what graphs are, including vertices, edges, directed and undirected graphs. It provides examples of graphs like social networks, transportation maps, and more. It covers basic graph terminology such as degree, regular graphs, subgraphs, walks, paths and cycles. It also discusses graph classes like trees, complete graphs and bipartite graphs. Finally, it touches on some historical graph problems, complexity analysis, centrality analysis, facility location problems and applications of graph theory.Shortest path algorithm



Shortest path algorithmsana younas
Ã˝
The document discusses several shortest path algorithms for graphs, including Dijkstra's algorithm, Bellman-Ford algorithm, and Floyd-Warshall algorithm. Dijkstra's algorithm finds the shortest path from a single source node to all other nodes in a graph with non-negative edge weights. Bellman-Ford can handle graphs with negative edge weights but is slower. Floyd-Warshall can find shortest paths in a graph between all pairs of nodes.Graph Theory



Graph TheoryRashmi Bhat
Ã˝
Graph theory is the study of graphs, which are mathematical structures used to model pairwise relationships between objects. A graph consists of vertices and edges that connect the vertices. Graph theory is used in computer science to model problems that can be represented as networks, such as determining routes in a city or designing circuits. It allows analyzing properties of graphs like connectivity and determining the minimum number of resources required. A graph can be represented using an adjacency matrix or adjacency list to store information about its vertices and edges.Introduction to Graph Theory



Introduction to Graph TheoryManash Kumar Mondal
Ã˝
Basic Graph Theory for Under Graduate level.Easy explanation of all beginner level topic regarding graph theory. I think it will help Graph Theory



Graph Theorykailash shaw
Ã˝
The document provides information about a faculty development program on discrete mathematics. It includes:
- An outline of the course content which covers topics like graph terminology, representations of graphs, connectivity, Euler and Hamilton paths, shortest path algorithms, planar graphs, and graph coloring.
- Details of learning resources including textbooks and reference books.
- A table listing the topics to be discussed in lectures, related self-learning tasks, reference materials and number of contact hours.
- Information on representation of graphs through adjacency matrix, incidence matrix and adjacency lists.
The program aims to teach key concepts in graph theory and related algorithms over 6 lecture hours through lectures, self-study and reference books.Cs6702 graph theory and applications 2 marks questions and answers



Cs6702 graph theory and applications 2 marks questions and answersappasami
Ã˝
Cs6702 graph theory and applications 2 marks questions and answers anna university CSE 7 seventh semesterFloyd Warshall Algorithm



Floyd Warshall AlgorithmInteX Research Lab
Ã˝
This document presents an overview of the Floyd-Warshall algorithm. It begins with an introduction to the algorithm, explaining that it finds shortest paths in a weighted graph with positive or negative edge weights. It then discusses the history and naming of the algorithm, attributed to researchers in the 1950s and 1960s. The document proceeds to provide an example of how the algorithm works, showing the distance and sequence tables that are updated over multiple iterations to find shortest paths between all pairs of vertices. It concludes with discussing the time and space complexity, applications, and references.Graph theory



Graph theoryThirunavukarasu Mani
Ã˝
This document provides an introduction to fundamental concepts in graph theory. It defines what a graph is composed of and different graph types including simple graphs, directed graphs, bipartite graphs, and complete graphs. It discusses graph terminology such as vertices, edges, paths, cycles, components, and subgraphs. It also covers graph properties like connectivity, degrees, isomorphism, and graph coloring. Examples are provided to illustrate key graph concepts and theorems are stated about properties of graphs like the Petersen graph and graph components.graph.ppt



graph.pptRakeshPandey951330
Ã˝
This document provides an introduction to graph theory. It defines key graph terminology like vertices, edges, directed and undirected graphs, paths, and connectivity. Examples are given to illustrate different graph types like trees, cycles, and complete graphs. Common graph representations like adjacency matrices and lists are also described. The document outlines theorems and properties of graphs, and discusses applications of graph theory concepts in areas like computer networks and chemistry.Graph representation



Graph representationTech_MX
Ã˝
A graph consists of vertices and edges, where vertices represent entities and edges represent relationships between vertices. Graphs can be represented sequentially using matrices like adjacency and incidence matrices, or linked using data structures like adjacency lists. Adjacency matrices allow fast addition/removal of edges but use more memory, while adjacency lists use less memory but are slower to modify. The best representation depends on whether the graph is dense or sparse.Graph coloring



Graph coloringRashika Ahuja
Ã˝
This document discusses graph coloring and its applications. It begins by defining graph coloring as assigning labels or colors to elements of a graph such that no two adjacent elements have the same color. It then provides examples of vertex coloring, edge coloring, and face coloring. The document also discusses the chromatic number and chromatic polynomial. It describes several real-world applications of graph coloring, including frequency assignment in cellular networks.Graphs in data structure



Graphs in data structurehamza javed
Ã˝
Graphs are a data structure composed of nodes connected by edges. There are two main types: directed graphs where edges show a flow between nodes, and undirected graphs where edges simply show a relationship between nodes. Key terminology includes adjacent nodes, paths, cyclic vs acyclic paths, and representations like adjacency matrices and lists. Graphs can model many real-world applications such as social networks, computer networks, road maps, and more.Graph-theory.ppt



Graph-theory.pptAlpaSinghRajput1
Ã˝
This document provides an introduction to graph theory, including basic terminology and concepts. It defines what a graph is mathematically as a collection of vertices and edges. It describes different types of graphs such as simple graphs, multiple graphs, weighted graphs, finite and infinite graphs, labeled graphs, and directed graphs. It also defines graph theory terms like adjacency, incidence, degree of a vertex, isomorphism, subgraphs, and graph operations like union and intersection. The document provides examples to illustrate each term and concept.Graph data structure and algorithms



Graph data structure and algorithmsAnandhasilambarasan D
Ã˝
This document discusses graph data structures and algorithms. A graph consists of nodes and edges, where nodes represent entities and edges represent relationships between nodes. There are different types of graphs including undirected, directed, weighted, and cyclic graphs. Graphs can be represented using an adjacency matrix or adjacency list. Graphs are used to model real-world networks and solve problems in areas like social networks, maps, robot path planning, and neural networks.Fleurys abas abbasli_



Fleurys abas abbasli_abas1333
Ã˝
Fleury's algorithm is a method for finding an Euler circuit or path in a graph. It starts at a vertex and chooses edges to traverse such that it never chooses a bridge edge unless it is the only option, in order to avoid disconnecting the graph. This ensures an Eulerian path or circuit can be found if one exists. The algorithm labels the edges as it traverses them to reconstruct the path or circuit. Applications include finding efficient routes for mail carriers or tourists.Distruct week 15 graphs theory (updated)



Distruct week 15 graphs theory (updated)Robert Almazan
Ã˝
Graph theory is the study of mathematical structures called graphs that are used to model pairwise relations between objects. Key concepts include vertices, edges, degrees, walks, paths, circuits, trees, planar graphs and non-planar graphs. Graph theory originated from Euler's solution to the Königsberg bridge problem in 1736. Important applications of graph theory include modeling networks, optimization problems, and molecular structures.More Related Content
What's hot (20)
Graph isomorphism



Graph isomorphismCore Condor
Ã˝
Graph isomorphism is the problem of determining whether two graphs are topologically identical. It is in NP but not known to be NP-complete. The refinement heuristic iteratively partitions vertices into equivalence classes to reduce possible mappings between graphs. For trees, there is a linear-time algorithm that labels vertices based on subtree structure to test rooted and unrooted tree isomorphism.Graph theory 



Graph theory iranian translate
Ã˝
This document provides an overview of graph theory and some of its common algorithms. It discusses the history of graph theory and its applications in various fields like engineering. It defines basic graph terminology like nodes, edges, walks, paths and cycles. It also explains popular graph algorithms like Dijkstra's algorithm for finding shortest paths, Kruskal's and Prim's algorithms for finding minimum spanning trees, and graph partitioning algorithms. It provides pseudocode, examples and analysis of the time complexity for these algorithms.Real life application



Real life applicationumadeviR3
Ã˝
Graph theory is the study of points and lines, and concepts like vertices and edges. It has many applications, including map coloring, Google Maps, and football games. Graph theory can be used to color maps with the minimum number of colors without any adjacent regions sharing the same color. It is also used in Google Maps for functions like estimating travel times and showing traffic conditions. In football, a match can be represented as a network with players as vertices and passes as edges, allowing analysis of things like which team has a more balanced network.Dijkstra's algorithm



Dijkstra's algorithmgsp1294
Ã˝
Dijkstra's algorithm finds the shortest paths from a source node to all other nodes in a graph. It works by maintaining two sets - one for nodes whose shortest paths are determined, and one for remaining nodes. It iteratively selects the node with the smallest distance from the source, calculates the distances to its neighbors, and moves them to the determined set until all nodes are processed. Some applications include finding fastest routes in transportation networks like road maps or flight schedules.Applications of graphs



Applications of graphsTech_MX
Ã˝
Graph theory has many applications including social networks, data organization, and communication networks. The document discusses Dijkstra's algorithm for finding the shortest path between nodes in a graph and its application to finding shortest routes between cities. It also discusses using graph representations for fingerprint classification, where fingerprints are modeled as graphs with nodes for fingerprint regions and edges between adjacent regions. Fingerprints are classified based on the structure of these graphs and compared to model graphs for matching.Kruskal Algorithm



Kruskal AlgorithmBhavik Vashi
Ã˝
Kruskal's algorithm is a minimum spanning tree algorithm that finds the minimum cost collection of edges that connect all vertices in a connected, undirected graph. It works by sorting the edges by weight and then sequentially adding the shortest edge that does not create a cycle. The algorithm uses a disjoint set data structure to track connected components in the graph. It runs in O(ElogE) time, where E is the number of edges.Introduction to Graph Theory



Introduction to Graph TheoryYosuke Mizutani
Ã˝
This document introduces the topic of graph theory. It defines what graphs are, including vertices, edges, directed and undirected graphs. It provides examples of graphs like social networks, transportation maps, and more. It covers basic graph terminology such as degree, regular graphs, subgraphs, walks, paths and cycles. It also discusses graph classes like trees, complete graphs and bipartite graphs. Finally, it touches on some historical graph problems, complexity analysis, centrality analysis, facility location problems and applications of graph theory.Shortest path algorithm



Shortest path algorithmsana younas
Ã˝
The document discusses several shortest path algorithms for graphs, including Dijkstra's algorithm, Bellman-Ford algorithm, and Floyd-Warshall algorithm. Dijkstra's algorithm finds the shortest path from a single source node to all other nodes in a graph with non-negative edge weights. Bellman-Ford can handle graphs with negative edge weights but is slower. Floyd-Warshall can find shortest paths in a graph between all pairs of nodes.Graph Theory



Graph TheoryRashmi Bhat
Ã˝
Graph theory is the study of graphs, which are mathematical structures used to model pairwise relationships between objects. A graph consists of vertices and edges that connect the vertices. Graph theory is used in computer science to model problems that can be represented as networks, such as determining routes in a city or designing circuits. It allows analyzing properties of graphs like connectivity and determining the minimum number of resources required. A graph can be represented using an adjacency matrix or adjacency list to store information about its vertices and edges.Introduction to Graph Theory



Introduction to Graph TheoryManash Kumar Mondal
Ã˝
Basic Graph Theory for Under Graduate level.Easy explanation of all beginner level topic regarding graph theory. I think it will help Graph Theory



Graph Theorykailash shaw
Ã˝
The document provides information about a faculty development program on discrete mathematics. It includes:
- An outline of the course content which covers topics like graph terminology, representations of graphs, connectivity, Euler and Hamilton paths, shortest path algorithms, planar graphs, and graph coloring.
- Details of learning resources including textbooks and reference books.
- A table listing the topics to be discussed in lectures, related self-learning tasks, reference materials and number of contact hours.
- Information on representation of graphs through adjacency matrix, incidence matrix and adjacency lists.
The program aims to teach key concepts in graph theory and related algorithms over 6 lecture hours through lectures, self-study and reference books.Cs6702 graph theory and applications 2 marks questions and answers



Cs6702 graph theory and applications 2 marks questions and answersappasami
Ã˝
Cs6702 graph theory and applications 2 marks questions and answers anna university CSE 7 seventh semesterFloyd Warshall Algorithm



Floyd Warshall AlgorithmInteX Research Lab
Ã˝
This document presents an overview of the Floyd-Warshall algorithm. It begins with an introduction to the algorithm, explaining that it finds shortest paths in a weighted graph with positive or negative edge weights. It then discusses the history and naming of the algorithm, attributed to researchers in the 1950s and 1960s. The document proceeds to provide an example of how the algorithm works, showing the distance and sequence tables that are updated over multiple iterations to find shortest paths between all pairs of vertices. It concludes with discussing the time and space complexity, applications, and references.Graph theory



Graph theoryThirunavukarasu Mani
Ã˝
This document provides an introduction to fundamental concepts in graph theory. It defines what a graph is composed of and different graph types including simple graphs, directed graphs, bipartite graphs, and complete graphs. It discusses graph terminology such as vertices, edges, paths, cycles, components, and subgraphs. It also covers graph properties like connectivity, degrees, isomorphism, and graph coloring. Examples are provided to illustrate key graph concepts and theorems are stated about properties of graphs like the Petersen graph and graph components.graph.ppt



graph.pptRakeshPandey951330
Ã˝
This document provides an introduction to graph theory. It defines key graph terminology like vertices, edges, directed and undirected graphs, paths, and connectivity. Examples are given to illustrate different graph types like trees, cycles, and complete graphs. Common graph representations like adjacency matrices and lists are also described. The document outlines theorems and properties of graphs, and discusses applications of graph theory concepts in areas like computer networks and chemistry.Graph representation



Graph representationTech_MX
Ã˝
A graph consists of vertices and edges, where vertices represent entities and edges represent relationships between vertices. Graphs can be represented sequentially using matrices like adjacency and incidence matrices, or linked using data structures like adjacency lists. Adjacency matrices allow fast addition/removal of edges but use more memory, while adjacency lists use less memory but are slower to modify. The best representation depends on whether the graph is dense or sparse.Graph coloring



Graph coloringRashika Ahuja
Ã˝
This document discusses graph coloring and its applications. It begins by defining graph coloring as assigning labels or colors to elements of a graph such that no two adjacent elements have the same color. It then provides examples of vertex coloring, edge coloring, and face coloring. The document also discusses the chromatic number and chromatic polynomial. It describes several real-world applications of graph coloring, including frequency assignment in cellular networks.Graphs in data structure



Graphs in data structurehamza javed
Ã˝
Graphs are a data structure composed of nodes connected by edges. There are two main types: directed graphs where edges show a flow between nodes, and undirected graphs where edges simply show a relationship between nodes. Key terminology includes adjacent nodes, paths, cyclic vs acyclic paths, and representations like adjacency matrices and lists. Graphs can model many real-world applications such as social networks, computer networks, road maps, and more.Graph-theory.ppt



Graph-theory.pptAlpaSinghRajput1
Ã˝
This document provides an introduction to graph theory, including basic terminology and concepts. It defines what a graph is mathematically as a collection of vertices and edges. It describes different types of graphs such as simple graphs, multiple graphs, weighted graphs, finite and infinite graphs, labeled graphs, and directed graphs. It also defines graph theory terms like adjacency, incidence, degree of a vertex, isomorphism, subgraphs, and graph operations like union and intersection. The document provides examples to illustrate each term and concept.Graph data structure and algorithms



Graph data structure and algorithmsAnandhasilambarasan D
Ã˝
This document discusses graph data structures and algorithms. A graph consists of nodes and edges, where nodes represent entities and edges represent relationships between nodes. There are different types of graphs including undirected, directed, weighted, and cyclic graphs. Graphs can be represented using an adjacency matrix or adjacency list. Graphs are used to model real-world networks and solve problems in areas like social networks, maps, robot path planning, and neural networks.Similar to Euler graph (20)
Fleurys abas abbasli_



Fleurys abas abbasli_abas1333
Ã˝
Fleury's algorithm is a method for finding an Euler circuit or path in a graph. It starts at a vertex and chooses edges to traverse such that it never chooses a bridge edge unless it is the only option, in order to avoid disconnecting the graph. This ensures an Eulerian path or circuit can be found if one exists. The algorithm labels the edges as it traverses them to reconstruct the path or circuit. Applications include finding efficient routes for mail carriers or tourists.Distruct week 15 graphs theory (updated)



Distruct week 15 graphs theory (updated)Robert Almazan
Ã˝
Graph theory is the study of mathematical structures called graphs that are used to model pairwise relations between objects. Key concepts include vertices, edges, degrees, walks, paths, circuits, trees, planar graphs and non-planar graphs. Graph theory originated from Euler's solution to the Königsberg bridge problem in 1736. Important applications of graph theory include modeling networks, optimization problems, and molecular structures.distructweek15graphstheoryupdated-160227143444.pdf



distructweek15graphstheoryupdated-160227143444.pdfansariparveen06
Ã˝
Graph theory is the study of mathematical structures called graphs that are used to model pairwise relations between objects. Key concepts include vertices, edges, degrees of vertices, walks, paths, circuits, subgraphs, complete graphs, planar graphs, Eulerian graphs, and Hamiltonian graphs. Graph theory has many applications including modeling networks, optimization problems, and molecular structures. The origins of graph theory can be traced back to Euler's solution to the Königsberg bridge problem in 1736.Graph theory



Graph theorymanikanta361
Ã˝
This document provides an introduction to graphs and graph terminology. It defines what a graph is composed of, including vertices and edges. It gives examples of graphs and has the student practice identifying vertices and edges. It also introduces common graph terminology like degree of a vertex, adjacent vertices, paths, circuits, bridges, Euler paths, and Euler circuits. Fleury's algorithm for finding an Euler circuit or path in a graph is described. The document uses examples and exercises to help students learn and practice applying these graph concepts.Koningsberg bridge problem



Koningsberg bridge problemSudiksha Joshi
Ã˝
The document describes the Konigsberg bridge problem and its solution by Euler. It discusses that Konigsberg (now Kaliningrad) had islands connected by seven bridges, and residents wondered if one could walk across each bridge once and return to their starting point. Euler proved this was impossible by modeling the problem as a graph with four vertices (land areas) and seven edges (bridges). He discovered all four vertices were odd degrees, meaning they were not traversable. The document also discusses how adding bridges could make the graph traversable and introduces basic graph theory concepts.Graph ds



Graph dsuniversity of Gujrat, pakistan
Ã˝
This document discusses key concepts in graph theory and algorithms for finding paths in graphs:
- It defines different types of graphs like simple graphs, directed graphs, and bipartite graphs.
- It explains representations of graphs using adjacency matrices and lists.
- It covers graph isomorphism, connected graphs, Euler paths and circuits, and Hamiltonian paths and cycles.
- It introduces the shortest path problem and Dijkstra's algorithm for finding the shortest path between vertices in a weighted graph.
- It provides an example applying Dijkstra's algorithm to find the shortest path between two vertices.Final-term Coverage.pptx. ..............



Final-term Coverage.pptx. ..............eustaquiojm1
Ã˝
The document discusses graphs and circuits on graphs. It defines key graph terminology like vertices, edges, walks, paths, circuits, connectedness, subgraphs, and Euler and Hamiltonian circuits. It presents theorems characterizing when a graph has an Euler circuit or Euler trail. For example, a graph has an Euler circuit if and only if it is connected and every vertex has even degree. It also provides examples and algorithms for determining if graphs have certain circuits.koningsbergproblem-140215072342-phpapp02 (1).pptx



koningsbergproblem-140215072342-phpapp02 (1).pptxAlpa Rajput
Ã˝
Euler proved that it is impossible to traverse all the bridges in Königsberg once each by inventing the mathematical graph. He showed that the Königsberg bridge network has 4 vertices, all with an odd number of edges, meaning it is not possible to start and end at the same location using each bridge only once. Adding an 8th bridge would make it possible by creating only 2 odd vertices. A graph is traversable if it has 0 or 2 vertices with an odd number of edges.Graph-Theory-and-Management-Science-2-Fleurys-Algorithm-and-Eulerizing.pptx



Graph-Theory-and-Management-Science-2-Fleurys-Algorithm-and-Eulerizing.pptxMuhammadMuqrrab1
Ã˝
This document discusses Fleury's algorithm, a method for finding an Euler path or circuit in a graph. It begins by defining key graph theory concepts like bridges, odd and even vertices. It then formally presents Fleury's algorithm, which starts at an odd vertex and traverses edges while avoiding bridges. An example applies the algorithm to find an Euler circuit. The document notes Fleury's algorithm is exhaustive, optimal, and efficient. It provides additional examples applying the algorithm and discusses Eulerizing graphs by adding edges to make all vertices even.Math



Mathblackbox90s
Ã˝
An Euler circuit is a trail that starts and ends at the same vertex and uses every edge in a graph exactly once. An Euler path starts and ends at different vertices and uses every edge once but may not visit every vertex. To determine if a graph contains an Euler circuit or path, one checks if every vertex has an even degree; if so, it contains an Euler circuit. For an Euler path, exactly two vertices may have an odd degree. Algorithms for finding these trails include picking a starting vertex and traversing edges, darkening used edges until all are traversed. A Hamilton circuit is similar but visits every vertex exactly once, returning to the starting point. A Hamilton path visits each vertex once without returning to the starting pointch10.5.pptx



ch10.5.pptxGauravGautam216125
Ã˝
This document section summarizes information about Euler paths and circuits as well as Hamilton paths and circuits. It discusses:
- Euler's solving of the Königsberg bridge problem and defining Euler paths/circuits
- Necessary and sufficient conditions for a graph to have an Euler path/circuit
- Algorithms for constructing Euler circuits
- Applications of Euler paths/circuits
- Defining Hamilton paths/circuits and discussing properties like Dirac's and Ore's theorems for Hamilton circuits
- Differences between Euler and Hamilton circuitsBridge problem : Discrete Structure 



Bridge problem : Discrete Structure Mitul Desai
Ã˝
This presentation briefs you with the bridge problem of Discrete Structure and solution to solve it using euler's theoremnossi ch 6



nossi ch 6lesaturner
Ã˝
The document discusses graphs and networks, including routing problems, routes and paths, connected graphs, weighted graphs, spanning trees, and minimal spanning trees. It provides examples and definitions of key concepts like vertices, edges, paths, circuits, connected graphs, weighted graphs, spanning trees, and minimal spanning trees. Kruskal's algorithm for finding a minimal spanning tree is also explained.Ds lec 5_chap4



Ds lec 5_chap4Self-Employed
Ã˝
This document discusses several graph theory concepts including:
- A connected undirected graph contains a simple path between any two vertices.
- Cut vertices and edges divide a graph into more components upon removal.
- Euler circuits and paths visit every edge exactly once in a connected multigraph.
- Planar graphs can be drawn in a plane without edge crossings.
- Graph coloring assigns colors to vertices such that no adjacent vertices share a color.Presentation on graphs



Presentation on graphsForwardBlog Enewzletter
Ã˝
The document defines key concepts in graph theory including:
- Types of graphs such as simple graphs, connected graphs, and regular graphs.
- Graph terminology like vertices, edges, walks, paths, and subgraphs.
- Special graphs like Hamiltonian and Euler graphs.
- Graph coloring problems including vertex coloring and edge coloring.
- Examples are given to illustrate graph concepts and properties.Depth first traversal(data structure algorithms)



Depth first traversal(data structure algorithms)bhuvaneshwariA5
Ã˝
The document discusses depth-first search (DFS) algorithms for graphs. It explains that DFS traverses a graph in a depthward motion using a stack. It explores all adjacent unvisited nodes, marks them as visited, and pushes them onto the stack before backtracking. The document provides pseudocode for DFS and an example of applying it to a graph. It also discusses uses of DFS in finding connected components, biconnectivity, and strongly connected components in graphs.Unit 2: All



Unit 2: AllHector Zenil
Ã˝
Graph theory is the study of graphs, which are mathematical structures used to model pairwise relations between objects. A graph consists of vertices and edges connecting pairs of vertices. There are many types of graphs including trees, which are connected acyclic graphs. Spanning trees are subgraphs of a graph that connect all vertices using the minimum number of edges. Key concepts in graph theory include paths, connectedness, cycles, and isomorphism between graphs.Graph algorithm



Graph algorithmUniversity of Potsdam
Ã˝
Algorithms for Sparse Graphs. An undirected graph G is a pair (V,E), where V is a finite set of points called vertices and E is a finite set of edges.Recently uploaded (20)
How Engineering Model Making Brings Designs to Life.pdf



How Engineering Model Making Brings Designs to Life.pdfMaadhu Creatives-Model Making Company
Ã˝
This PDF highlights how engineering model making helps turn designs into functional prototypes, aiding in visualization, testing, and refinement. It covers different types of models used in industries like architecture, automotive, and aerospace, emphasizing cost and time efficiency.Best KNow Hydrogen Fuel Production in the World The cost in USD kwh for H2



Best KNow Hydrogen Fuel Production in the World The cost in USD kwh for H2Daniel Donatelli
Ã˝
The cost in USD/kwh for H2
Daniel Donatelli
Secure Supplies Group
Index
• Introduction - Page 3
• The Need for Hydrogen Fueling - Page 5
• Pure H2 Fueling Technology - Page 7
• Blend Gas Fueling: A Transition Strategy - Page 10
• Performance Metrics: H2 vs. Fossil Fuels - Page 12
• Cost Analysis and Economic Viability - Page 15
• Innovations Driving Leadership - Page 18
• Laminar Flame Speed Adjustment
• Heat Management Systems
• The Donatelli Cycle
• Non-Carnot Cycle Applications
• Case Studies and Real-World Applications - Page 22
• Conclusion: Secure Supplies’ Leadership in Hydrogen Fueling - Page 27
Lessons learned when managing MySQL in the Cloud



Lessons learned when managing MySQL in the CloudIgor Donchovski
Ã˝
Managing MySQL in the cloud introduces a new set of challenges compared to traditional on-premises setups, from ensuring optimal performance to handling unexpected outages. In this article, we delve into covering topics such as performance tuning, cost-effective scalability, and maintaining high availability. We also explore the importance of monitoring, automation, and best practices for disaster recovery to minimize downtime.Multi objective genetic approach with Ranking



Multi objective genetic approach with Rankingnamisha18
Ã˝
Multi objective genetic approach with Ranking decarbonization steel industry rev1.pptx



decarbonization steel industry rev1.pptxgonzalezolabarriaped
Ã˝
Webinar Decarbonization steel industryUS Patented ReGenX Generator, ReGen-X Quatum Motor EV Regenerative Accelerati...



US Patented ReGenX Generator, ReGen-X Quatum Motor EV Regenerative Accelerati...Thane Heins NOBEL PRIZE WINNING ENERGY RESEARCHER
Ã˝
Preface: The ReGenX Generator innovation operates with a US Patented Frequency Dependent Load
Current Delay which delays the creation and storage of created Electromagnetic Field Energy around
the exterior of the generator coil. The result is the created and Time Delayed Electromagnetic Field
Energy performs any magnitude of Positive Electro-Mechanical Work at infinite efficiency on the
generator's Rotating Magnetic Field, increasing its Kinetic Energy and increasing the Kinetic Energy of
an EV or ICE Vehicle to any magnitude without requiring any Externally Supplied Input Energy. In
Electricity Generation applications the ReGenX Generator innovation now allows all electricity to be
generated at infinite efficiency requiring zero Input Energy, zero Input Energy Cost, while producing
zero Greenhouse Gas Emissions, zero Air Pollution and zero Nuclear Waste during the Electricity
Generation Phase. In Electric Motor operation the ReGen-X Quantum Motor now allows any
magnitude of Work to be performed with zero Electric Input Energy.
Demonstration Protocol: The demonstration protocol involves three prototypes;
1. Protytpe #1, demonstrates the ReGenX Generator's Load Current Time Delay when compared
to the instantaneous Load Current Sine Wave for a Conventional Generator Coil.
2. In the Conventional Faraday Generator operation the created Electromagnetic Field Energy
performs Negative Work at infinite efficiency and it reduces the Kinetic Energy of the system.
3. The Magnitude of the Negative Work / System Kinetic Energy Reduction (in Joules) is equal to
the Magnitude of the created Electromagnetic Field Energy (also in Joules).
4. When the Conventional Faraday Generator is placed On-Load, Negative Work is performed and
the speed of the system decreases according to Lenz's Law of Induction.
5. In order to maintain the System Speed and the Electric Power magnitude to the Loads,
additional Input Power must be supplied to the Prime Mover and additional Mechanical Input
Power must be supplied to the Generator's Drive Shaft.
6. For example, if 100 Watts of Electric Power is delivered to the Load by the Faraday Generator,
an additional >100 Watts of Mechanical Input Power must be supplied to the Generator's Drive
Shaft by the Prime Mover.
7. If 1 MW of Electric Power is delivered to the Load by the Faraday Generator, an additional >1
MW Watts of Mechanical Input Power must be supplied to the Generator's Drive Shaft by the
Prime Mover.
8. Generally speaking the ratio is 2 Watts of Mechanical Input Power to every 1 Watt of Electric
Output Power generated.
9. The increase in Drive Shaft Mechanical Input Power is provided by the Prime Mover and the
Input Energy Source which powers the Prime Mover.
10. In the Heins ReGenX Generator operation the created and Time Delayed Electromagnetic Field
Energy performs Positive Work at infinite efficiency and it increases the Kinetic Energy of the
system.
Structural QA/QC Inspection in KRP 401600 | Copper Processing Plant-3 (MOF-3)...



Structural QA/QC Inspection in KRP 401600 | Copper Processing Plant-3 (MOF-3)...slayshadow705
Ã˝
This presentation provides an in-depth analysis of structural quality control in the KRP 401600 section of the Copper Processing Plant-3 (MOF-3) in Uzbekistan. As a Structural QA/QC Inspector, I have identified critical welding defects, alignment issues, bolting problems, and joint fit-up concerns.
Key topics covered:
✔ Common Structural Defects – Welding porosity, misalignment, bolting errors, and more.
✔ Root Cause Analysis – Understanding why these defects occur.
✔ Corrective & Preventive Actions – Effective solutions to improve quality.
✔ Team Responsibilities – Roles of supervisors, welders, fitters, and QC inspectors.
✔ Inspection & Quality Control Enhancements – Advanced techniques for defect detection.
üìå Applicable Standards: GOST, KMK, SNK ‚Äì Ensuring compliance with international quality benchmarks.
üöÄ This presentation is a must-watch for:
‚úÖ QA/QC Inspectors, Structural Engineers, Welding Inspectors, and Project Managers in the construction & oil & gas industries.
‚úÖ Professionals looking to improve quality control processes in large-scale industrial projects.
üì¢ Download & share your thoughts! Let's discuss best practices for enhancing structural integrity in industrial projects.
Categories:
Engineering
Construction
Quality Control
Welding Inspection
Project Management
Tags:
#QAQC #StructuralInspection #WeldingDefects #BoltingIssues #ConstructionQuality #Engineering #GOSTStandards #WeldingInspection #QualityControl #ProjectManagement #MOF3 #CopperProcessing #StructuralEngineering #NDT #OilAndGasIntegration of Additive Manufacturing (AM) with IoT : A Smart Manufacturing A...



Integration of Additive Manufacturing (AM) with IoT : A Smart Manufacturing A...ASHISHDESAI85
Ã˝
Combining 3D printing with Internet of Things (IoT) enables the creation of smart, connected, and customizable objects that can monitor, control, and optimize their performance, potentially revolutionizing various industries. oT-enabled 3D printers can use sensors to monitor the quality of prints during the printing process. If any defects or deviations from the desired specifications are detected, the printer can adjust its parameters in real time to ensure that the final product meets the required standards.Air pollution is contamination of the indoor or outdoor environment by any ch...



Air pollution is contamination of the indoor or outdoor environment by any ch...dhanashree78
Ã˝
Air pollution is contamination of the indoor or outdoor environment by any chemical, physical or biological agent that modifies the natural characteristics of the atmosphere.
Household combustion devices, motor vehicles, industrial facilities and forest fires are common sources of air pollution. Pollutants of major public health concern include particulate matter, carbon monoxide, ozone, nitrogen dioxide and sulfur dioxide. Outdoor and indoor air pollution cause respiratory and other diseases and are important sources of morbidity and mortality.
WHO data show that almost all of the global population (99%) breathe air that exceeds WHO guideline limits and contains high levels of pollutants, with low- and middle-income countries suffering from the highest exposures.
Air quality is closely linked to the earth’s climate and ecosystems globally. Many of the drivers of air pollution (i.e. combustion of fossil fuels) are also sources of greenhouse gas emissions. Policies to reduce air pollution, therefore, offer a win-win strategy for both climate and health, lowering the burden of disease attributable to air pollution, as well as contributing to the near- and long-term mitigation of climate change.
UNIT 1FUNDAMENTALS OF OPERATING SYSTEMS.pptx



UNIT 1FUNDAMENTALS OF OPERATING SYSTEMS.pptxKesavanT10
Ã˝
UNIT 1FUNDAMENTALS OF OPERATING SYSTEMS.pptxUnit II: Design of Static Equipment Foundations



Unit II: Design of Static Equipment FoundationsSanjivani College of Engineering, Kopargaon
Ã˝
Design of Static Equipment, that is vertical vessels foundation.Gauges are a Pump's Best Friend - Troubleshooting and Operations - v.07



Gauges are a Pump's Best Friend - Troubleshooting and Operations - v.07Brian Gongol
Ã˝
No reputable doctor would try to conduct a basic physical exam without the help of a stethoscope. That's because the stethoscope is the best tool for gaining a basic "look" inside the key systems of the human body. Gauges perform a similar function for pumping systems, allowing technicians to "see" inside the pump without having to break anything open. Knowing what to do with the information gained takes practice and systemic thinking. This is a primer in how to do that.US Patented ReGenX Generator, ReGen-X Quatum Motor EV Regenerative Accelerati...



US Patented ReGenX Generator, ReGen-X Quatum Motor EV Regenerative Accelerati...Thane Heins NOBEL PRIZE WINNING ENERGY RESEARCHER
Ã˝
Euler graph
- 1. EULER GRAPH PRESENTED : AAQIB ASHRAF PARREY
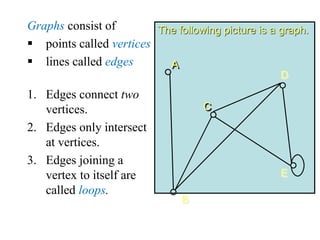
- 2. Graphs consist of ÔÇß points called vertices ÔÇß lines called edges 1. Edges connect two vertices. 2. Edges only intersect at vertices. 3. Edges joining a vertex to itself are called loops. The following picture is a graph. A B C D E
- 3. EULER GRAPH • A graph is called Eulerian if it has an Eulerian Cycle and called Semi-Eulerian if it has an Eulerian Path. An Eulerian cycle (path) is a sub_graph Ge = (V;Ee) of G = (V;E) which passes exactly once through each edge of G. G must thus be connected and all vertices V are visited (perhaps more than once). We then says that G is Eulerian
- 4. Euler Circuit and Euler path • When a graph has no vertices of odd degree, then it has at least one Euler circuit. • When a graph has exactly two vertices of odd degree, then it has at least one Euler path. • When a graph has more than two vertices of odd degree, then – There is no Euler circuit or Euler path – There is no possible way that we can travel along all the edges of the graph without having to cross some of them more than once.
- 5. Euler circuit & Euler path • How we will find a route that covers all the edges of the graph while revisiting the least possible number of edges (deadhead travel)? • In real-world problems, The cost is proportional to the amount of travel. • Total cost of a route = cost of traveling original edges in the graph + cost of deadhead travel
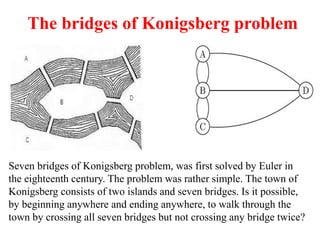
- 6. The bridges of Konigsberg problem Seven bridges of Konigsberg problem, was first solved by Euler in the eighteenth century. The problem was rather simple. The town of Konigsberg consists of two islands and seven bridges. Is it possible, by beginning anywhere and ending anywhere, to walk through the town by crossing all seven bridges but not crossing any bridge twice?
- 7. Eulerizing a graph • Modifying a graph by adding extra edges in such a way that the odd vertices become even vertices. • The process of changing a graph by adding additional edges so that odd vertices are eliminated is called Eulerizing the graph. • Note: The edges that we add must be duplicates of edges that already exist. The idea is to cover the edges of the original graph in the best possible way without creating any new.
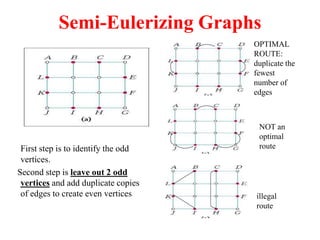
- 8. Eulerizing Graphs First step is to identify the odd vertices. Second step is to add duplicate copies of edges to create all even vertices OPTIMAL ROUTE: duplicate the fewest number of edges NOT an optimal route illegal route
- 9. Semi- eularization of the graph • We are not required to start and end at the same vertex. • We duplicate as many edges as needed to eliminate all odd vertices except for two, which we allow to remain odd. • We then use one of the odd vertices as the starting point and we will end up to the other odd vertex.
- 10. Semi-Eulerizing Graphs First step is to identify the odd vertices. Second step is leave out 2 odd vertices and add duplicate copies of edges to create even vertices OPTIMAL ROUTE: duplicate the fewest number of edges NOT an optimal route illegal route
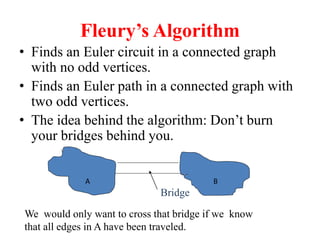
- 11. Fleury’s Algorithm • Finds an Euler circuit in a connected graph with no odd vertices. • Finds an Euler path in a connected graph with two odd vertices. • The idea behind the algorithm: Don’t burn your bridges behind you. A B Bridge We would only want to cross that bridge if we know that all edges in A have been traveled.
- 12. Fleury’s Algorithm • Let G be an Eulerian graph. • STEP 1: Choose any vertex v of G and set current vertex equal to v and current trail equal to the empty sequence of edges. • STEP 2: Select any edge e incident with the current vertex but choosing a bridge only if there is no alternative. • STEP 3: Add e to the current trail and set the current vertex equal to the vertex at the ‘other end’ of e. [If e is a loop, the current vertex will not move.] • STEP 4: Delete e from the graph. Delete any isolated vertices. • Repeat steps 2 – 4 until all edges have been deleted from G. The final current trail is an Eulerian trail in G.
- 13. Fleury’s Theorem • Every time we traverse another edge, we erase it from copy 1 but mark (red) and level it with the appropriate number on copy 2. • Copy 1 gets smaller and cop2 gets redder. • Copy 1 helps us decide where to go next; copy 2 helps us reconstruct our trip. Copy 1 A B C D E F B C D E F Copy 2 Start at F (arbitrarily)
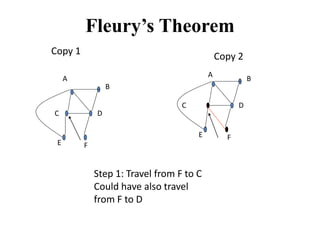
- 14. Fleury’s Theorem Copy 1 B C D E F A B C D E F Copy 2 Step 1: Travel from F to C Could have also travel from F to D A
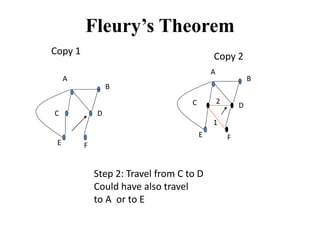
- 15. Fleury’s Theorem Copy 1 B C D E F A B C D E F Copy 2 Step 2: Travel from C to D Could have also travel to A or to E 1 2 A
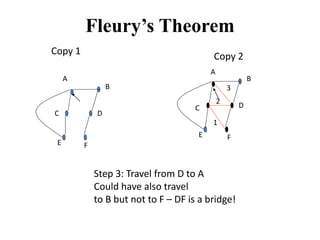
- 16. Fleury’s Theorem Copy 1 B C D E F A B C D E F Copy 2 Step 3: Travel from D to A Could have also travel to B but not to F – DF is a bridge! 1 2 A 3
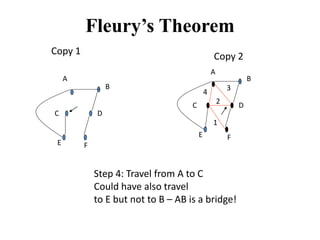
- 17. Fleury’s Theorem Copy 1 B C D E F A B C D E F Copy 2 Step 4: Travel from A to C Could have also travel to E but not to B – AB is a bridge! 1 2 A 3 4
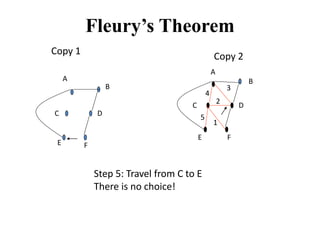
- 18. Fleury’s Theorem Copy 1 B C D E F A B C D E F Copy 2 Step 5: Travel from C to E There is no choice! 1 2 A 3 4 5
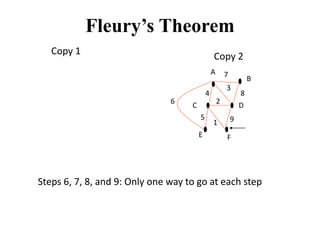
- 19. Fleury’s Theorem Copy 1 B C D E F Copy 2 Steps 6, 7, 8, and 9: Only one way to go at each step 1 2 A 3 4 5 6 7 8 9
- 20. Fleury’s Algorithm for finding Euler circuit • First make sure that the graph is connected and all the vertices have even degree. • Pick any vertex as the stating point • When you have a choice, always choose to travel along an edge that is not a bridge of the yet-to-be- traveled part of the graph • Label the edges in the order in which we travel them • When we cannot travel any more, stop. we are done.
- 21. APPLICATIONS • Chinese postman problem • Communicating networks • Tourist guide
- 22. Thank you









