EVHEN. –ź—Ā–ł–ľ–ľ–Ķ—ā—Ä–ł—á–Ĺ—č–Ļ SPN-—ą–ł—Ą—Ä –Ĺ–į –Ī–į–∑–Ķ white-box-–ļ—Ä–ł–Ņ—ā–ĺ–≥—Ä–į—Ą–ł–ł –ł —Ö–į–ĺ—ā–ł—á–Ķ—Ā–ļ–ł—Ö –ĺ—ā–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ļ
- 1. –ź–°–ė–ú–ú–ē–Ę–†–ė–ß–Ě–ę–ô SPN-–®–ė–§–† –Ě–ź –Ď–ź–ó–ē WHITE-BOX-–ö–†–ė–ü–Ę–ě–ď–†–ź–§–ė–ė –ė –•–ź–ě–Ę–ė–ß–ē–°–ö–ė–• –ě–Ę–ě–Ď–†–ź–Ė–ē–Ě–ė–ô –ļ.—ā.–Ĺ, –©–Ķ–Ľ–ļ—É–Ĺ–ĺ–≤ –Ē.–ź. –ö–§ –ú–ď–Ę–£ –ł–ľ–Ķ–Ĺ–ł –Ě.–≠. –Ď–į—É–ľ–į–Ĺ–į
- 2. White-box-–ļ—Ä–ł–Ņ—ā–ĺ–≥—Ä–į—Ą–ł—Ź ‚úď–Ě–į–Ī–ĺ—Ä —ā–Ķ—Ö–Ĺ–ł–ļ, –Ņ–ĺ–∑–≤–ĺ–Ľ—Ź—é—Č–ł—Ö –Ņ—Ä–Ķ–ĺ–Ī—Ä–į–∑–ĺ–≤–į—ā—Ć —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł—á–Ĺ—č–Ļ –Ī–Ľ–ĺ—á–Ĺ—č–Ļ —ą–ł—Ą—Ä –≤ –į—Ā–ł–ľ–ľ–Ķ—ā—Ä–ł—á–Ĺ—č–Ļ –Ņ–ĺ—Ā—Ä–Ķ–ī—Ā—ā–≤–ĺ–ľ —Ā–ĺ–ļ—Ä—č—ā–ł—Ź –ļ–Ľ—é—á–į –≤ —Ä–Ķ–į–Ľ–ł–∑–į—Ü–ł–ł –į–Ľ–≥–ĺ—Ä–ł—ā–ľ–į —ą–ł—Ą—Ä–ĺ–≤–į–Ĺ–ł—Ź ‚úď–ü—Ä–Ķ–ī–Ĺ–į–∑–Ĺ–į—á–Ķ–Ĺ–į –ī–Ľ—Ź —Ā–ĺ–∑–ī–į–Ĺ–ł—Ź –Ī—č—Ā—ā—Ä—č—Ö –į—Ā–ł–ľ–ľ–Ķ—ā—Ä–ł—á–Ĺ—č—Ö —ą–ł—Ą—Ä–ĺ–≤, –Ņ–ĺ–∑–≤–ĺ–Ľ—Ź—é—Č–ł—Ö –ł —ą–ł—Ą—Ä–ĺ–≤–į—ā—Ć, –ł –Ņ–ĺ–ī–Ņ–ł—Ā—č–≤–į—ā—Ć —Ā–ĺ–ĺ–Ī—Č–Ķ–Ĺ–ł—Ź ‚úď–í —Ā–Ľ—É—á–į–Ķ —Ā—ā–ĺ–Ļ–ļ–ĺ–Ļ –ł –Ī—č—Ā—ā—Ä–ĺ–Ļ —Ä–Ķ–į–Ľ–ł–∑–į—Ü–ł–ł –Ņ–ĺ–∑–≤–ĺ–Ľ–ł—ā —Ā—É—Č–Ķ—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ —É–Ņ—Ä–ĺ—Ā—ā–ł—ā—Ć –ł —Ā–ī–Ķ–Ľ–į—ā—Ć –Ī–ĺ–Ľ–Ķ–Ķ –Ī–Ķ–∑–ĺ–Ņ–į—Ā–Ĺ—č–ľ–ł –Ņ—Ä–ĺ—ā–ĺ–ļ–ĺ–Ľ—č –ĺ–Ī–ľ–Ķ–Ĺ–į –∑–į—ą–ł—Ą—Ä–ĺ–≤–į–Ĺ–Ĺ–ĺ–Ļ –ł–Ĺ—Ą–ĺ—Ä–ľ–į—Ü–ł–Ķ–Ļ (–≤ —á–į—Ā—ā–Ĺ–ĺ—Ā—ā–ł, –ĺ—ā–Ņ–į–ī—Ď—ā –Ĺ–Ķ–ĺ–Ī—Ö–ĺ–ī–ł–ľ–ĺ—Ā—ā—Ć –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į—ā—Ć –į–Ľ–≥–ĺ—Ä–ł—ā–ľ –Ē–ł—Ą—Ą–ł-–•–Ķ–Ľ–Ľ–ľ–į–Ĺ–į) ‚úď–Ď—č—Ā—ā—Ä—č–Ļ –Ī–Ķ–∑–ĺ–Ņ–į—Ā–Ĺ—č–Ļ –ĺ–Ī–ľ–Ķ–Ĺ –ľ–Ķ–∂–ī—É 3-–ľ—Ź –ł –Ī–ĺ–Ľ–Ķ–Ķ –į–Ī–ĺ–Ĺ–Ķ–Ĺ—ā–į–ľ–ł —Ā –Ņ–ĺ–ī—ā–≤–Ķ—Ä–∂–ī–Ķ–Ĺ–ł–Ķ–ľ –į–≤—ā–ĺ—Ä—Ā—ā–≤–į —Ā–ĺ–ĺ–Ī—Č–Ķ–Ĺ–ł–Ļ
- 3. –ü—Ä–Ķ–ī—č–ī—É—Č–ł–Ķ –ł—Ā—Ā–Ľ–Ķ–ī–ĺ–≤–į–Ĺ–ł—Ź ‚úďChow S., Eisen P., Johnson H., Van Oorschot P.C. (2003), White-Box Cryptography and an AES Implementation. In: Nyberg K., Heys H. (eds) Selected Areas in Cryptography. SAC 2002. Lecture Notes in Computer Science, vol 2595. Springer, Berlin, Heidelberg ‚úďOlivier Billet and Henri Gilbert. A Traceable Block Cipher. In Advances in Cryptology - ASIACRYPT 2003, volume 2894 of Lecture Notes in Computer Science, pages 331-346. Springer-Verlag, 2003 ‚úďOlivier Billet, Henri Gilbert, and Charaf Ech-Chatbi. Cryptanalysis of a White-Box AES Implementation. In Proceedings of the 11th International Workshop on Selected Areas in Cryptography (SAC 2004), volume 3357 of Lecture Notes in Computer Science, pages 227‚Äď240. Springer-Verlag, 2004. ‚úďBrecht Wyseur, White-box cryptography, PhD thesis, March 2009 ‚úďDmitry Schelkunov, White-Box Cryptography and SPN ciphers. LRC method, Cryptology ePrint Archive: Report 2010/419 ‚úďBrecht Wyseur, White-box cryptography: hiding keys in software, MISC magazine, April 2012 ‚úďJoppe W. Bos and Charles Hubain and Wil Michiels and Philippe Teuwen, Differential Computation Analysis: Hiding your White-Box Designs is Not Enough, Cryptology ePrint Archive: Report 2015/753
- 4. –ź—ā–į–ļ–ł –Ĺ–į white-box-—Ä–Ķ–į–Ľ–ł–∑–į—Ü–ł–ł –ü—Ä–į–ļ—ā–ł—á–Ķ—Ā–ļ–ł –≤–ĺ –≤—Ā–Ķ—Ö white-box-—Ä–Ķ–į–Ľ–ł–∑–į—Ü–ł—Ź—Ö –ł–∑–≤–Ķ—Ā—ā–Ĺ—č –Ľ–ł–Ĺ–Ķ–Ļ–Ĺ–į—Ź –ł –Ĺ–Ķ–Ľ–ł–Ĺ–Ķ–Ļ–Ĺ–į—Ź —á–į—Ā—ā–ł –ł—Ā—Ö–ĺ–ī–Ĺ–ĺ–≥–ĺ –į–Ľ–≥–ĺ—Ä–ł—ā–ľ–į –ī–Ľ—Ź –ļ–į–∂–ī–ĺ–≥–ĺ –ł–∑ —Ä–į—É–Ĺ–ī–ĺ–≤. –Ě–Ķ–ĺ–Ī—Ö–ĺ–ī–ł–ľ–ĺ ¬ę–ĺ—ā–ī–Ķ–Ľ–ł—ā—ƬĽ white-box-–Ņ—Ä–Ķ–ĺ–Ī—Ä–į–∑–ĺ–≤–į–Ĺ–ł—Ź ‚úď–Ē–ł—Ą—Ą–Ķ—Ä–Ķ–Ĺ—Ü–ł–į–Ľ—Ć–Ĺ—č–Ļ –ļ—Ä–ł–Ņ—ā–ĺ–į–Ĺ–į–Ľ–ł–∑ (–≤ —ā–ĺ–ľ —á–ł—Ā–Ľ–Ķ fault injection) ‚úď–ź–Ľ–≥–Ķ–Ī—Ä–į–ł—á–Ķ—Ā–ļ–ł–Ļ –ļ—Ä–ł–Ņ—ā–ĺ–į–Ĺ–į–Ľ–ł–∑ ‚úď–ė–∑–≤–Ľ–Ķ—á–Ķ–Ĺ–ł–Ķ –Ĺ–Ķ–Ľ–ł–Ĺ–Ķ–Ļ–Ĺ–ĺ–Ļ —á–į—Ā—ā–ł (Olivier Billet, Henri Gilbert, and Charaf Ech-Chatbi. Cryptanalysis of a White-Box AES Implementation)
- 5. –ú–Ķ—ā–ĺ–ī —Ā–ĺ–ļ—Ä—č—ā–ł—Ź –Ľ–ł–Ĺ–Ķ–Ļ–Ĺ–ĺ–Ļ –∑–į–≤–ł—Ā–ł–ľ–ĺ—Ā—ā–ł (1) )))(mod)(mod(( ))(mod))(mod(( 122 211 ÔÉģ ÔÉ≠ Ôɨ ÔÉóÔÉóÔÄĹ ÔÉóÔÉóÔÄĹ ppcbax pcpbax 21, pp ‚Äď –Ĺ–Ķ–Ņ—Ä–ł–≤–ĺ–ī–ł–ľ—č–Ķ –Ņ–ĺ–Ľ–ł–Ĺ–ĺ–ľ—č n-–Ļ —Ā—ā–Ķ–Ņ–Ķ–Ĺ–ł, –į 21,,,, xxcba - –Ņ–ĺ–Ľ–ł–Ĺ–ĺ–ľ—č —Ā—ā–Ķ–Ņ–Ķ–Ĺ–Ķ–Ļ, –ľ–Ķ–Ĺ—Ć—ą–ł—Ö n. 21 xx ÔāĻ
- 8. –ú–Ķ—ā–ĺ–ī —Ā–ĺ–ļ—Ä—č—ā–ł—Ź –Ľ–ł–Ĺ–Ķ–Ļ–Ĺ–ĺ–Ļ –∑–į–≤–ł—Ā–ł–ľ–ĺ—Ā—ā–ł c–ła–Ĺ–į–Ļ—ā–ł–Ĺ–Ķ–ĺ–Ī—Ö–ĺ–ī–ł–ľ–ĺxy–łxy–ī–į–Ĺ–Ĺ—č–ľ–Ņ–ĺ–ó–į–ī–į—á–į p dqpdcxs q p bqpbaxs q p cxs q p axs q qpdqpdcxsxy qpbqpbaxsxy pdqpcxsxy pbqpaxsxy )()(: ')( ; )( ; )( '; )( )4( ')()( )()( )3( )(mod)')(()( )(mod))(()( 21 3 11 3 2 11 2 1 1 1 1 33112 22111 3112 2111 ÔÉļ ÔÉĽ ÔÉļ ÔÉ™ ÔÉę ÔÉ™ ÔÉóÔÉóÔÄ≠ÔÉóÔÉó ÔÄĹÔÉļ ÔÉĽ ÔÉļ ÔÉ™ ÔÉę ÔÉ™ ÔÉóÔÉóÔÄ≠ÔÉóÔÉó ÔÄĹÔÉļ ÔÉĽ ÔÉļ ÔÉ™ ÔÉę ÔÉ™ ÔÉó ÔÄĹÔÉļ ÔÉĽ ÔÉļ ÔÉ™ ÔÉę ÔÉ™ ÔÉó ÔÄĹ ÔÉģ ÔÉ≠ Ôɨ ÔÉóÔÄ≠ÔÉóÔÉóÔÄ≠ÔÉóÔÉóÔÄĹ ÔÉóÔÄ≠ÔÉóÔÉóÔÄ≠ÔÉóÔÉóÔÄĹ ÔÉģ ÔÉ≠ Ôɨ ÔÉóÔÉóÔÄ≠ÔÉóÔÄĹ ÔÉóÔÉóÔÄ≠ÔÉóÔÄĹ RLWE?
- 9. –ú–Ķ—ā–ĺ–ī —Ā–ĺ–ļ—Ä—č—ā–ł—Ź –Ľ–ł–Ĺ–Ķ–Ļ–Ĺ–ĺ–Ļ –∑–į–≤–ł—Ā–ł–ľ–ĺ—Ā—ā–ł –£—Ā–Ľ–ĺ–∂–Ĺ–ł–ľ —Ą–ĺ—Ä–ľ—É–Ľ—É (2) (5) )(mod)...)(mod))(mod)((...()( )(mod)...)(mod))(mod)((...()( )()()0( 3 )0( 12 )()()0( 2 )0( 11 ÔÉģ ÔÉ≠ Ôɨ ÔÉóÔÉóÔÉóÔÄĹ ÔÉóÔÉóÔÉóÔÄĹ k v k k u k pdpdpcxsxy pbpbpaxsxy )()( ÔĀ°ÔĀ° jppi ÔāĻ ÔÄ® ÔÄ© )!2,2min(:–°–Ľ–ĺ–∂–Ĺ–ĺ—Ā—ā—Ć 2)1(2 nkn ÔÄę
- 10. –Ę–Ķ–ĺ—Ä–ł—Ź —Ö–į–ĺ—Ā–į –≤ –ļ—Ä–ł–Ņ—ā–ĺ–≥—Ä–į—Ą–ł–ł ‚úďGoce Jakimoski and Ljupňáco Kocarev, Chaos and Cryptography: Block Encryption Ciphers Based on Chaotic Maps. IEEE TRANSACTIONS ON CIRCUITS AND SYSTEMS‚ÄĒI: FUNDAMENTAL THEORY AND APPLICATIONS, VOL. 48, NO. 2, FEBRUARY 2001 ‚úďAsim, M., Jeoti, V.: Efficient and simple method for designing chaotic S-boxes. ETRI Journal 30(1), 170‚Äď172 (2008) ‚úďMona Dara and Kooroush Manochehri, A Novel Method for Designing S-Boxes Based on Chaotic Logistic Maps Using Cipher Key. World Applied Sciences Journal 28 (12): 2003-2009, 2013 ‚úďChristopher A. Wood, Chaos-Based Symmetric Key Cryptosystems ‚úďDragan Lambińá and Miodrag ŇĹivkovińá, COMPARISON OF RANDOM S-BOX GENERATION METHODS. PUBLICATIONS DE L‚ÄôINSTITUT MATH√ČMATIQUE Nouvelle s√©rie, tome 93 (107) (2013)
- 11. –°–ĺ–∑–ī–į–Ĺ–ł–Ķ S-box-–ĺ–≤ —Ā –Ņ–ĺ–ľ–ĺ—Č—Ć—é —Ö–į–ĺ—ā–ł—á–Ķ—Ā–ļ–ł—Ö –ĺ—ā–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ļ ‚úď–•–ĺ—Ä–ĺ—ą–ł–Ķ –ļ—Ä–ł–Ņ—ā–ĺ–≥—Ä–į—Ą–ł—á–Ķ—Ā–ļ–ł–Ķ —Ā–≤–ĺ–Ļ—Ā—ā–≤–į –Ņ–ĺ —Ä–Ķ–∑—É–Ľ—Ć—ā–į—ā–į–ľ —Ü–Ķ–Ľ–ĺ–≥–ĺ —Ä—Ź–ī–į –ł—Ā—Ā–Ľ–Ķ–ī–ĺ–≤–į–Ĺ–ł–Ļ ‚úď–ü—Ä–ĺ—Ā—ā—č–Ķ –į–Ľ–≥–ĺ—Ä–ł—ā–ľ—č ‚úď–°–Ľ—É—á–į–Ļ–Ĺ–ĺ—Ā—ā—Ć –ĺ—ā–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ļ –≤ —Ā–ĺ—á–Ķ—ā–į–Ĺ–ł–ł —Ā —Ö–ĺ—Ä–ĺ—ą–ł–ľ–ł –ļ—Ä–ł–Ņ—ā–ĺ–≥—Ä–į—Ą–ł—á–Ķ—Ā–ļ–ł–ľ–ł —Ā–≤–ĺ–Ļ—Ā—ā–≤–į–ľ–ł –Ņ–ĺ–≤—č—ą–į–Ķ—ā —É—Ä–ĺ–≤–Ķ–Ĺ—Ć –Ī–Ķ–∑–ĺ–Ņ–į—Ā–Ĺ–ĺ—Ā—ā–ł
- 12. –ö–ĺ–ī—č —Ā –ľ–į–ļ—Ā–ł–ľ–į–Ľ—Ć–Ĺ–ĺ–Ļ –ī–ł—Ā—ā–į–Ĺ—Ü–ł–Ķ–Ļ. MDS-–ľ–į—ā—Ä–ł—Ü–į MDS-–ľ–į—ā—Ä–ł—Ü–į (Maximal Distance Separable matrix) ‚Äď –Ņ—Ä–ĺ–≤–Ķ—Ä–ĺ—á–Ĺ–į—Ź –ľ–į—ā—Ä–ł—Ü–į –Ľ–ł–Ĺ–Ķ–Ļ–Ĺ–ĺ–≥–ĺ –Ī–Ľ–ĺ–ļ–ĺ–≤–ĺ–≥–ĺ –ļ–ĺ–ī–į —Ā –ľ–į–ļ—Ā–ł–ľ–į–Ľ—Ć–Ĺ–ĺ–Ļ –ī–ł—Ā—ā–į–Ĺ—Ü–ł–Ķ–Ļ ‚ó¶ –ě–Ī–Ķ—Ā–Ņ–Ķ—á–ł–≤–į–Ķ—ā –ľ–į–ļ—Ā–ł–ľ–į–Ľ—Ć–Ĺ–ĺ–Ķ —Ä–į—Ā—Ā–Ķ–ł–≤–į–Ĺ–ł–Ķ –∑–į —Ā—á—Ď—ā —Ā–≤–ĺ–Ķ–Ļ —Ā—ā—Ä—É–ļ—ā—É—Ä—č ‚ó¶ –ė—Ā–Ņ–ĺ–Ľ—Ć–∑—É–Ķ—ā—Ā—Ź –Ņ—Ä–ł —Ā–ĺ–∑–ī–į–Ĺ–ł–ł SPN-—ą–ł—Ą—Ä–ĺ–≤ –≤ –ļ–į—á–Ķ—Ā—ā–≤–Ķ –Ľ–ł–Ĺ–Ķ–Ļ–Ĺ—č—Ö —Ä–į—Ā—Ā–Ķ–ł–≤–į—é—Č–ł—Ö –Ņ—Ä–Ķ–ĺ–Ī—Ä–į–∑–ĺ–≤–į–Ĺ–ł–Ļ ‚ó¶ –ė–Ĺ—ā–Ķ—Ä–Ķ—Ā–Ĺ—č–Ķ —ā–ł–Ņ—č –ľ–į—ā—Ä–ł—Ü: ‚ó¶ –ú–į—ā—Ä–ł—Ü–į –í–į–Ĺ–ī–Ķ—Ä–ľ–ĺ–Ĺ–ī–į ‚ó¶ –ė–Ĺ–≤–ĺ–Ľ—é—ā–ł–≤–Ĺ–į—Ź –ľ–į—ā—Ä–ł—Ü–į (–ĺ–ī–Ĺ–į –ł —ā–į –∂–Ķ MDS-–ľ–į—ā—Ä–ł—Ü–į –ī–Ľ—Ź —ą–ł—Ą—Ä–ĺ–≤–į–Ĺ–ł—Ź –ł —Ä–į—Ā—ą–ł—Ą—Ä–ĺ–≤–į–Ĺ–ł—Ź) ‚ó¶ –ú–į—ā—Ä–ł—Ü–į –ö–ĺ—ą–ł ‚ó¶ –¶–ł—Ä–ļ—É–Ľ—Ź—Ä–Ĺ–į—Ź –ľ–į—ā—Ä–ł—Ü–į (–ļ–į–ļ –≤ Rijndael)
- 13. –ú–į—ā—Ä–ł—Ü–į –ö–ĺ—ą–ł ‚úď–Į–≤–Ľ—Ź–Ķ—ā—Ā—Ź MDS-–ľ–į—ā—Ä–ł—Ü–Ķ–Ļ ‚úď–õ—Ď–≥–ļ–ł–Ļ –į–Ľ–≥–ĺ—Ä–ł—ā–ľ —Ā–ĺ–∑–ī–į–Ĺ–ł—Ź –Ĺ–Ķ–∑–į–≤–ł—Ā–ł–ľ–ĺ –ĺ—ā —Ä–į–∑–ľ–Ķ—Ä–Ĺ–ĺ—Ā—ā–ł ‚úď–°–≤–ĺ–Ļ—Ā—ā–≤–ĺ —Ü–ł—Ä–ļ—É–Ľ—Ź—Ä–Ĺ–ĺ—Ā—ā–ł –Ĺ–Ķ –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ–ł–į–Ľ—Ć–Ĺ–ĺ –ī–Ľ—Ź white-box-—Ä–Ķ–į–Ľ–ł–∑–į—Ü–ł–ł ‚úď–°–≤–ĺ–Ļ—Ā—ā–≤–ĺ –ł–Ĺ–≤–ĺ–Ľ—é—ā–ł–≤–Ĺ–ĺ—Ā—ā–ł –≤—Ä–Ķ–ī–Ĺ–ĺ –ī–Ľ—Ź white-box-—Ä–Ķ–į–Ľ–ł–∑–į—Ü–ł–ł ‚úď–°–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ, –≤—č–Ī–ł—Ä–į–Ķ–ľ –ľ–į—ā—Ä–ł—Ü—É –ö–ĺ—ą–ł ÔÄ® ÔÄ© ÔÄ® ÔÄ©k ijjijijiij GFayxnjmiyxyxa 2,,;0;0;0; 1 ÔÉéÔÄľÔā£ÔÄľÔā£ÔāĻÔÄęÔÄęÔÄĹ ÔÄ≠
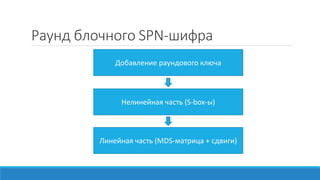
- 14. –†–į—É–Ĺ–ī –Ī–Ľ–ĺ—á–Ĺ–ĺ–≥–ĺ SPN-—ą–ł—Ą—Ä–į –Ě–Ķ–Ľ–ł–Ĺ–Ķ–Ļ–Ĺ–į—Ź —á–į—Ā—ā—Ć (S-box-—č) –Ē–ĺ–Ī–į–≤–Ľ–Ķ–Ĺ–ł–Ķ —Ä–į—É–Ĺ–ī–ĺ–≤–ĺ–≥–ĺ –ļ–Ľ—é—á–į –õ–ł–Ĺ–Ķ–Ļ–Ĺ–į—Ź —á–į—Ā—ā—Ć (MDS-–ľ–į—ā—Ä–ł—Ü–į + —Ā–ī–≤–ł–≥–ł)
- 15. –†–į—É–Ĺ–ī SPN-—ą–ł—Ą—Ä–į –ł T-box-—č (–Ĺ–į –Ņ—Ä–ł–ľ–Ķ—Ä–Ķ AES-128)
- 16. –•–į–ĺ—ā–ł—á–Ĺ—č–Ļ –į—Ā–ł–ľ–ľ–Ķ—ā—Ä–ł—á–Ĺ—č–Ļ white-box-—ą–ł—Ą—Ä ‚úď–Ę–į–Ī–Ľ–ł—Ü—č –Ņ–ĺ–ī—Ā—ā–į–Ĺ–ĺ–≤–ĺ–ļ (8x8 –Ī–ł—ā) —Ā–ĺ–∑–ī–į—é—ā—Ā—Ź —Ö–į–ĺ—ā–ł—á–Ķ—Ā–ļ–ł –ī–Ľ—Ź –ļ–į–∂–ī–ĺ–≥–ĺ –ł–∑ –≤—Ö–ĺ–ī–Ĺ—č—Ö –Ī–į–Ļ—ā–ĺ–≤ –ļ–į–∂–ī–ĺ–≥–ĺ —Ä–į—É–Ĺ–ī–į ‚úďMDS-–ľ–į—ā—Ä–ł—Ü–į (16x16 –Ī–į–Ļ—ā) —Ā–ĺ–∑–ī–į—Ď—ā—Ā—Ź —Ö–į–ĺ—ā–ł—á–Ķ—Ā–ļ–ł (–ľ–į—ā—Ä–ł—Ü–į –ö–ĺ—ą–ł) ‚úď–Ē–Ľ—Ź white-box-—Ä–Ķ–į–Ľ–ł–∑–į—Ü–ł–ł –ł—Ā–Ņ–ĺ–Ľ—Ć–∑—É–Ķ—ā—Ā—Ź —Ä–Ķ–į–Ľ–ł–∑–į—Ü–ł—Ź SPN-—ą–ł—Ą—Ä–į —Ā –Ņ–ĺ–ľ–ĺ—Č—Ć—é T-box-–ĺ–≤ ‚úď–õ–ł–Ĺ–Ķ–Ļ–Ĺ–į—Ź –∑–į–≤–ł—Ā–ł–ľ–ĺ—Ā—ā—Ć –ľ–Ķ–∂–ī—É —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā–į–ľ–ł T-box-–ĺ–≤ —Ā–ļ—Ä—č–≤–į–Ķ—ā—Ā—Ź —Ā –Ņ–ĺ–ľ–ĺ—Č—Ć—é –≤—č—ą–Ķ–ĺ–Ņ–ł—Ā–į–Ĺ–Ĺ–ĺ–≥–ĺ –ľ–Ķ—ā–ĺ–ī–į —Ā–ĺ–ļ—Ä—č—ā–ł—Ź –Ľ–ł–Ĺ–Ķ–Ļ–Ĺ–ĺ–Ļ –∑–į–≤–ł—Ā–ł–ľ–ĺ—Ā—ā–ł ‚úď–Ě–į–Ī–ĺ—Ä –ľ–ĺ–ī–ł—Ą–ł—Ü–ł—Ä–ĺ–≤–į–Ĺ–Ĺ—č—Ö —ā–į–Ī–Ľ–ł—Ü (T-box-–ĺ–≤) ‚Äď –ĺ—ā–ļ—Ä—č—ā—č–Ļ –ļ–Ľ—é—á —ą–ł—Ą—Ä–ĺ–≤–į–Ĺ–ł—Ź. –ü–ĺ –Ĺ–ł–ľ —Ā–Ľ–ĺ–∂–Ĺ–ĺ –≤–ĺ—Ā—Ā—ā–į–Ĺ–ĺ–≤–ł—ā—Ć –∑–į–ļ—Ä—č—ā—č–Ļ –ļ–Ľ—é—á ‚Äď –Ĺ–į–Ī–ĺ—Ä —ā–į–Ī–Ľ–ł—Ü –ī–Ľ—Ź —Ä–į—Ā—ą–ł—Ą—Ä–ĺ–≤–į–Ĺ–ł—Ź
- 17. –†–į—É–Ĺ–ī —ą–ł—Ą—Ä–į )6( ))((( ... ))((( ))((( ... ))((( ... ))((( ))((( ))((( ... ))((( ))((( ... )15( 1 )15()15,315()15( )15( 1 )15()15,1()1( )15( 1 )15()15,0()0( )1( 1 )1()1,15()15( )1( 1 )1()1,1()1( )1( 1 )1()1,0()0( )0( 1 )0()0,15()15( )0( 1 )0()0,1()1( )0( 1 )0()0,0()0( )15( )1( )0( ÔÉļ ÔÉļ ÔÉļ ÔÉļ ÔÉļ ÔÉĽ ÔÉĻ ÔÉ™ ÔÉ™ ÔÉ™ ÔÉ™ ÔÉ™ ÔÉę ÔÉ© ÔÉÖÔÉÖ ÔÉļ ÔÉļ ÔÉļ ÔÉļ ÔÉļ ÔÉĽ ÔÉĻ ÔÉ™ ÔÉ™ ÔÉ™ ÔÉ™ ÔÉ™ ÔÉę ÔÉ© ÔÉÖ ÔÉļ ÔÉļ ÔÉļ ÔÉļ ÔÉļ ÔÉĽ ÔÉĻ ÔÉ™ ÔÉ™ ÔÉ™ ÔÉ™ ÔÉ™ ÔÉę ÔÉ© ÔÄĹ ÔÉļ ÔÉļ ÔÉļ ÔÉļ ÔÉļ ÔÉĽ ÔÉĻ ÔÉ™ ÔÉ™ ÔÉ™ ÔÉ™ ÔÉ™ ÔÉę ÔÉ© ÔÄĹ ÔÄ≠ ÔÄ≠ ÔÄ≠ ÔÄ≠ ÔÄ≠ ÔÄ≠ ÔÄ≠ ÔÄ≠ ÔÄ≠ jjjj jjjj jjjj jjjj jjjj jjjj jjjj jjjj jjjj j j j j ystmix ystmix ystmix ystmix ystmix ystmix ystmix ystmix ystmix y y y Y (i) j-y 1 -–Ī–į–Ļ—ā –≤—č—Ö–ĺ–ī–Ĺ—č—Ö –ī–į–Ĺ–Ĺ—č—Ö –ł–∑ –Ņ—Ä–Ķ–ī—č–ī—É—Č–Ķ–≥–ĺ —Ä–į—É–Ĺ–ī–į. –ē—Ā–Ľ–ł 0ÔÄĹj , —ā–ĺ (i) j-y 1 - –Ī–į–Ļ—ā –ł—Ā—Ö–ĺ–ī–Ĺ–ĺ–≥–ĺ —Ā–ĺ–ĺ–Ī—Č–Ķ–Ĺ–ł—Ź. )(k js - —ć—ā–ĺ —ā–į–Ī–Ľ–ł—Ü–į –Ņ–ĺ–ī—Ā—ā–į–Ĺ–ĺ–≤–ĺ–ļ, —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤—É—é—Č–į—Ź –ļ–į–∂–ī–ĺ–ľ—É –≤—Ö–ĺ–ī–Ĺ–ĺ–ľ—É –Ī–į–Ļ—ā—É. )(l,k jt - —É–ľ–Ĺ–ĺ–∂–Ķ–Ĺ–ł–Ķ –Ĺ–į —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā —Ā—ā—Ä–ĺ–ļ–ł —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤—É—é—Č–Ķ–Ļ MDS-–ľ–į—ā—Ä–ł—Ü—č –≤ )GF( 8 2 . )k( jmix - –∑–į–Ņ—É—ā—č–≤–į—é—Č–ł–Ķ –Ņ—Ä–Ķ–ĺ–Ī—Ä–į–∑–ĺ–≤–į–Ĺ–ł—Ź –Ĺ–į –Ī–į–∑–Ķ –ľ–Ķ—ā–ĺ–ī–į —Ā–ĺ–ļ—Ä—č—ā–ł—Ź –Ľ–ł–Ĺ–Ķ–Ļ–Ĺ–ĺ–Ļ –∑–į–≤–ł—Ā–ł–ľ–ĺ—Ā—ā–ł
- 18. –ú–į—Ā–ļ–ł—Ä–ĺ–≤–ļ–į –Ľ–ł–Ĺ–Ķ–Ļ–Ĺ–ĺ–Ļ –∑–į–≤–ł—Ā–ł–ľ–ĺ—Ā—ā–ł –ľ–Ķ–∂–ī—É —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā–į–ľ–ł T-box-–į )7( )(mod)...)(mod))(mod)(((...( .......................................................................... )(mod)...)(mod))(mod)(((...( )(mod)...)(mod))(mod)(((...( )(mod)...)(mod))(mod)(((...( )(mod)...)(mod))(mod)(((...( ][' ),(),()1,()1,()0,()0,()( 3 ),3(),3()1,3()1,3()0,3()0,3()3( 2 ),2(),2()1,2()1,2()0,2()0,2()2( 1 ),1(),1()1,1()1,1()0,1()0,1()1( 0 ),0(),0()1,0()1,0()0,0()0,0()0( 33 22 11 00 ÔÉļ ÔÉļ ÔÉļ ÔÉļ ÔÉļ ÔÉļ ÔÉļ ÔÉļ ÔÉĽ ÔÉĻ ÔÉ™ ÔÉ™ ÔÉ™ ÔÉ™ ÔÉ™ ÔÉ™ ÔÉ™ ÔÉ™ ÔÉę ÔÉ© ÔÉÖÔÉóÔÉóÔÉó ÔÉÖÔÉóÔÉóÔÉó ÔÉÖÔÉóÔÉóÔÉó ÔÉÖÔÉóÔÉóÔÉó ÔÉÖÔÉóÔÉóÔÉó ÔÄĹ n kn i kn i n i n i n i n i n i k i k iiiiii k i k iiiiii k i k iiiiii k i k iiiiii i valpbpbpbat valpbpbpbat valpbpbpbat valpbpbpbat valpbpbpbat aT nn )( j it - —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā T-box-–į –ī–ĺ –Ņ—Ä–ł–ľ–Ķ–Ĺ–Ķ–Ĺ–ł—Ź –∑–į–Ņ—É—ā—č–≤–į—é—Č–ł—Ö –Ņ—Ä–Ķ–ĺ–Ī—Ä–į–∑–ĺ–≤–į–Ĺ–ł–Ļ (mix), ),( uj ib ‚Äď —Ā–Ľ—É—á–į–Ļ–Ĺ–ĺ –≤—č–Ī—Ä–į–Ĺ–Ĺ—č–Ļ –Ņ–ĺ–Ľ–ł–Ĺ–ĺ–ľ –≤ )2( h GF , ),( uj ip ‚Äď —Ā–Ľ—É—á–į–Ļ–Ĺ–ĺ –≤—č–Ī—Ä–į–Ĺ–Ĺ—č–Ļ –Ĺ–Ķ–Ņ—Ä–ł–≤–ĺ–ī–ł–ľ—č–Ļ –Ņ–ĺ–Ľ–ł–Ĺ–ĺ–ľ h-–Ļ —Ā—ā–Ķ–Ņ–Ķ–Ĺ–ł –Ĺ–į–ī )2(GF ),(),1(),0( ... vn i v i v i ppp ÔāĻÔāĻÔāĻ
- 19. EVHEN. –•–į–ĺ—ā–ł—á–Ĺ—č–Ļ –į—Ā–ł–ľ–ľ–Ķ—ā—Ä–ł—á–Ĺ—č–Ļ white-box-—ą–ł—Ą—Ä ‚úď–Ě–į–∑–≤–į–Ĺ –≤ —á–Ķ—Ā—ā—Ć –ī–≤—É—Ö –≤–Ķ–Ľ–ł—á–į–Ļ—ą–ł—Ö –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–ĺ–≤: –≠–≤–į—Ä–ł—Ā—ā–į –ď–į–Ľ—É–į –ł –ź–Ĺ—Ä–ł –ü—É–į–Ĺ–ļ–į—Ä–Ķ ‚úď–ě–Ī–Ľ–į–ī–į–Ķ—ā —Ā–ļ–ĺ—Ä–ĺ—Ā—ā—Ć—é —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł—á–Ĺ–ĺ–≥–ĺ —ą–ł—Ą—Ä–į ‚úď–ü–ĺ–∑–≤–ĺ–Ľ—Ź–Ķ—ā –ł —ą–ł—Ą—Ä–ĺ–≤–į—ā—Ć, –ł –Ņ–ĺ–ī–Ņ–ł—Ā—č–≤–į—ā—Ć ‚úď–†–į–∑–ľ–Ķ—Ä –ĺ—ā–ļ—Ä—č—ā–ĺ–≥–ĺ –ļ–Ľ—é—á–į: 640 –ö–Ī ‚úď–Ě–ł–∑–ļ–ł–Ķ —ā—Ä–Ķ–Ī–ĺ–≤–į–Ĺ–ł—Ź –ļ –≤—č—á–ł—Ā–Ľ–ł—ā–Ķ–Ľ—Ć–Ĺ—č–ľ —Ä–Ķ—Ā—É—Ä—Ā–į–ľ: –ĺ–ī–ł–Ĺ —Ä–į—É–Ĺ–ī ‚Äď 16 –ĺ–Ņ–Ķ—Ä–į—Ü–ł–Ļ —Ā–Ľ–ĺ–∂–Ķ–Ĺ–ł—Ź –Ņ–ĺ –ľ–ĺ–ī—É–Ľ—é 2 16-–ł –Ī–į–Ļ—ā–ĺ–≤—č—Ö —á–ł—Ā–Ķ–Ľ. –Ě—É–∂–Ĺ–ĺ –≤—Ā–Ķ–≥–ĺ 3 –ĺ–Ņ–Ķ—Ä–į—Ü–ł–ł: –≤—č–Ī–ĺ—Ä–ļ–į –ł–∑ –Ņ–į–ľ—Ź—ā–ł, —Ā–Ľ–ĺ–∂–Ķ–Ĺ–ł–Ķ –Ņ–ĺ –ľ–ĺ–ī—É–Ľ—é 2 –ł –∑–į–Ņ–ł—Ā—Ć –≤ –Ņ–į–ľ—Ź—ā—Ć
- 20. –ü—Ä–ł–ľ–Ķ–Ĺ–Ķ–Ĺ–ł–Ķ ‚úďIoT ‚úďDRM ‚úď–í–Ķ–∑–ī–Ķ, –≥–ī–Ķ –Ĺ—É–∂–Ĺ–į –Ī—č—Ā—ā—Ä–į—Ź –ł –Ĺ–Ķ —ā—Ä–Ķ–Ī–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ–į—Ź –ļ –≤—č—á–ł—Ā–Ľ–ł—ā–Ķ–Ľ—Ć–Ĺ—č–ľ —Ä–Ķ—Ā—É—Ä—Ā–į–ľ –į—Ā–ł–ľ–ľ–Ķ—ā—Ä–ł—á–Ĺ–į—Ź –ļ—Ä–ł–Ņ—ā–ĺ–≥—Ä–į—Ą–ł—Ź
- 21. –°–Ņ–į—Ā–ł–Ī–ĺ –∑–į –≤–Ĺ–ł–ľ–į–Ĺ–ł–Ķ –ė—Ā—Ö–ĺ–ī–Ĺ—č–Ļ –ļ–ĺ–ī —Ä–Ķ–į–Ľ–ł–∑–į—Ü–ł–ł EVHEN: https://github.com/dmschelkunov/EVHEN –Ď–Ľ–ĺ–≥ –į–≤—ā–ĺ—Ä–į: http://dschelkunov.blogspot.com E-mail –į–≤—ā–ĺ—Ä–į: d.schelkunov@gmail.com

















![–ú–į—Ā–ļ–ł—Ä–ĺ–≤–ļ–į –Ľ–ł–Ĺ–Ķ–Ļ–Ĺ–ĺ–Ļ –∑–į–≤–ł—Ā–ł–ľ–ĺ—Ā—ā–ł
–ľ–Ķ–∂–ī—É —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā–į–ľ–ł T-box-–į
)7(
)(mod)...)(mod))(mod)(((...(
..........................................................................
)(mod)...)(mod))(mod)(((...(
)(mod)...)(mod))(mod)(((...(
)(mod)...)(mod))(mod)(((...(
)(mod)...)(mod))(mod)(((...(
]['
),(),()1,()1,()0,()0,()(
3
),3(),3()1,3()1,3()0,3()0,3()3(
2
),2(),2()1,2()1,2()0,2()0,2()2(
1
),1(),1()1,1()1,1()0,1()0,1()1(
0
),0(),0()1,0()1,0()0,0()0,0()0(
33
22
11
00
ÔÉļ
ÔÉļ
ÔÉļ
ÔÉļ
ÔÉļ
ÔÉļ
ÔÉļ
ÔÉļ
ÔÉĽ
ÔÉĻ
ÔÉ™
ÔÉ™
ÔÉ™
ÔÉ™
ÔÉ™
ÔÉ™
ÔÉ™
ÔÉ™
ÔÉę
ÔÉ©
ÔÉÖÔÉóÔÉóÔÉó
ÔÉÖÔÉóÔÉóÔÉó
ÔÉÖÔÉóÔÉóÔÉó
ÔÉÖÔÉóÔÉóÔÉó
ÔÉÖÔÉóÔÉóÔÉó
ÔÄĹ
n
kn
i
kn
i
n
i
n
i
n
i
n
i
n
i
k
i
k
iiiiii
k
i
k
iiiiii
k
i
k
iiiiii
k
i
k
iiiiii
i
valpbpbpbat
valpbpbpbat
valpbpbpbat
valpbpbpbat
valpbpbpbat
aT
nn
)( j
it - —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā T-box-–į –ī–ĺ –Ņ—Ä–ł–ľ–Ķ–Ĺ–Ķ–Ĺ–ł—Ź –∑–į–Ņ—É—ā—č–≤–į—é—Č–ł—Ö –Ņ—Ä–Ķ–ĺ–Ī—Ä–į–∑–ĺ–≤–į–Ĺ–ł–Ļ (mix), ),( uj
ib ‚Äď
—Ā–Ľ—É—á–į–Ļ–Ĺ–ĺ –≤—č–Ī—Ä–į–Ĺ–Ĺ—č–Ļ –Ņ–ĺ–Ľ–ł–Ĺ–ĺ–ľ –≤ )2( h
GF , ),( uj
ip ‚Äď —Ā–Ľ—É—á–į–Ļ–Ĺ–ĺ –≤—č–Ī—Ä–į–Ĺ–Ĺ—č–Ļ –Ĺ–Ķ–Ņ—Ä–ł–≤–ĺ–ī–ł–ľ—č–Ļ
–Ņ–ĺ–Ľ–ł–Ĺ–ĺ–ľ h-–Ļ —Ā—ā–Ķ–Ņ–Ķ–Ĺ–ł –Ĺ–į–ī )2(GF
),(),1(),0(
... vn
i
v
i
v
i ppp ÔāĻÔāĻÔāĻ](https://image.slidesharecdn.com/2017-170403185309/85/EVHEN-SPN-white-box-18-320.jpg)


