Evolute and involute
Download as PPTX, PDF
5 likes6,614 views
The document defines an evolute and involute as two space curves where the tangent at each point on one curve is perpendicular to the corresponding point on the other. Specifically, if a curve C is the evolute of C1, then C1 will lie on the tangent surface of C and their tangent vectors will be perpendicular. The evolute and involute have a reciprocal relationship where knowing one determines the other.
Evolute and involute
- 1. Evolute and Involute Let and 1 are two one-one correspondence space curves such that tangent at any point on is a normal to the corresponding point on 1 then C is called evolute of 1 and 1 is called involute of . i.e. if C is evolute of 1 then a. 1 lies in the tangent surface of C b. tangent vectors to and 1 are perpendicular
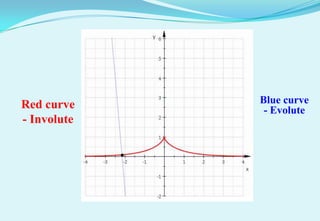
- 2. Red curve Blue curve - Evolute - Involute
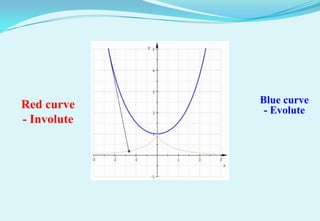
- 3. Red curve Blue curve - Evolute - Involute
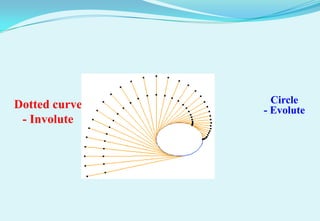
- 4. Dotted curve Circle - Evolute - Involute