Exact Algorithms for Minimum Edge Dominating Set and Lowest Edge Dominating Set
- 1. Exact Algorithms for Minimum Edge Dominating Set and Lowest Edge Dominating Set Discrete Mathematics Lab. Ken Iwaide February 18, 2016 2016 2 18
- 2. 平成28年度 数理工学専攻説明会 第1回: 平成28年5月7日(土) 第2回: 平成28年5月30日(月) 場所,プログラムの詳細は以下の専攻HPを見てください. http://www.amp.i.kyoto-u.ac.jp 研究室見学できます.在学生から,入試勉強のしかた, 過去問の勉強方法などを聞くチャンスです. 京都大学大学院 情報学研究科 数理工学専攻 修士課程,博士課程の学生募集
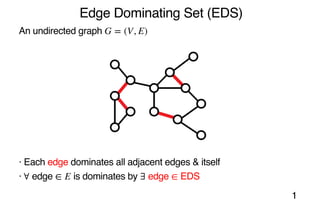
- 3. Edge Dominating Set (EDS) An undirected graph · Each edge dominates all adjacent edges & itself · edge is dominates by edge EDS 1
- 4. Outline 1. An algorithm solving Minimum EDS in time & Parameterized EDS in time 2. An algorithm solving Lowest EDS in time 2
- 5. NP-Hard Problems for EDS Previous Time BoundsMinimum EDS Input: An -vertex graph Output: A minimum EDS of [Xiao & Nagamochi 2012] Parameterized EDS Input: An -vertex graph & an integer Output: Does have an EDS of size ? · Fast for small [Iwaide & Nagamochi 2015] 3
- 6. Previous Algorithms Minimum EDS Authors Time Bound Year Raman et al. 2007 Fomin et al. (exp. space) 2009 Van Rooij & Bodlaender 2008 Xiao & Nagamochi 2012 Parameterized EDS Fernau 2006 Fomin et al. (exp. space) 2009 Binkele-Raible & Fernau 2012 Xiao et al. 2013 Iwaide & Nagamochi 2015 4
- 7. Branching Algorithm Select a vertex to decide Branch on used as an endpoint of EDS 1. 2. not used All neighbors of are used as endpoints· All vertices are decided (leaf node) “minimum” EDS can be found in polynomial time [van Rooij & Bodlaender 2008] 5
- 8. Branching Algorithm Select a vertex to decide Branch on used as an endpoint of EDS 1. 2. not used All neighbors of are used as endpoints· All vertices are decided (leaf node) “minimum” EDS can be found in polynomial time [van Rooij & Bodlaender 2008] : measure Time bound 6
- 9. NP-Hard Problems for EDS Previous Time BoundsMinimum EDS Input: An -vertex graph Output: A minimum EDS of [Xiao & Nagamochi 2012] Parameterized EDS Input: An -vertex graph & an integer Output: Does have an EDS of size ? · Fast for small [Iwaide & Nagamochi 2015] How fast can solve? 7
- 10. NP-Hard Problems for EDS Previous Time BoundsMinimum EDS Input: An -vertex graph Output: A minimum EDS of [Xiao & Nagamochi 2012] Parameterized EDS Input: An -vertex graph & an integer Output: Does have an EDS of size ? · Fast for small [Iwaide & Nagamochi 2015] How fast can solve? Our Purpose · Design an algorithm solving both problems with currently best time ? time & time 8
- 11. Additional Selection Criteria : measure for ??? Parameterized EDS Note: # · Criteria to select a vertex · Flexibility · Keep decrement of measure time · Introduce further criteria for time : measure for ???? Minimum EDS Note: # Better decrement of ? 9
- 12. Outline 1. An algorithm solving Minimum EDS in time & Parameterized EDS in time 2. An algorithm solving Lowest EDS in time 10
- 13. Lowest Solution Vertex Cover (VC) and Maximum Matching (MM) Note: MM can be found in polynomial time VC MM · To find a minimum VC NP-hard · VC with VC MM ? in polynomial time [Gavril 1977] Lowest case is easy for some NP-hard problem 11
- 14. Lower Bound on EDS · is a lower bound on EDSMM EDS Endpoints of EDS become VC EDS VC MMLowest EDS Input: An -vertex graph Output: Does have an EDS of size ?MM Note: special case of Parameterized EDS with MM · Solvable in polynomial time? Prove the NP-completeness · Solvable faster than time of PEDS? ? Design an -time algorithm 12
- 15. Properties of Lowest EDS We revealed the following properties · Case MM is “odd”: reducible into “even” cases “odd”? ?“even”? ?“even” #edges · Case MM is “even”: edge LEDS dominates exactly two edges MM edge MM is dominated by exactly one egde LEDS New Reduction rules Better time bound 13
- 16. Conclusions & Future Work · Designed a polynomial-space algorithm solving Minimum EDS in time & Parameterized EDS in time · Proved the NP-completeness of Lowest EDS · Designed a polynomial-space algorithm solving Lowest EDS in time · For , efficiently solvable whether ? EDS of size MM ? 14
- 17. 15
- 18. Minimum EDS by PEDS Algorithm · Minimum Independent EDS Minimum EDS [Yannakakis & Gavril 1980] : minimum size of EDS of found by a PEDS algorithm in poly. time Case 1. minimum EDS that contains Case 2. minimum EDS that contains 16
- 19. NP-Completeness of Lowest EDS 1-In-3 3SAT NP-hard [Garey & Johnson 1979] Input: A set of variables & a set of clauses on s.t. each clause has exactly three literals Output: assignment on s.t. each clause has exactly one true literal? · Polynomial-time reduction to Lowest EDS 17
- 20. Application · Evaluating the worst-case performance of trunking Switch Shared lines Nodes Occupied / Vacant lines Bipartite graph · Line is busy Occupied lines become a maximal matching of · Minimum maximal matching Minimum EDS [Yannakakis & Gavril 1980] 18




![NP-Hard Problems for EDS
Previous Time BoundsMinimum EDS
Input: An -vertex graph
Output: A minimum EDS of [Xiao & Nagamochi 2012]
Parameterized EDS
Input: An -vertex graph & an integer
Output: Does have an EDS of size ?
· Fast for small
[Iwaide & Nagamochi 2015]
3](https://image.slidesharecdn.com/2016a-160308033053/85/Exact-Algorithms-for-Minimum-Edge-Dominating-Set-and-Lowest-Edge-Dominating-Set-5-320.jpg)

![Branching Algorithm
Select a vertex
to decide
Branch on
used as
an endpoint of EDS
1.
2. not used
All neighbors of are
used as endpoints· All vertices are decided (leaf node)
“minimum” EDS can be found in polynomial time
[van Rooij & Bodlaender 2008]
5](https://image.slidesharecdn.com/2016a-160308033053/85/Exact-Algorithms-for-Minimum-Edge-Dominating-Set-and-Lowest-Edge-Dominating-Set-7-320.jpg)
![Branching Algorithm
Select a vertex
to decide
Branch on
used as
an endpoint of EDS
1.
2. not used
All neighbors of are
used as endpoints· All vertices are decided (leaf node)
“minimum” EDS can be found in polynomial time
[van Rooij & Bodlaender 2008]
: measure
Time bound
6](https://image.slidesharecdn.com/2016a-160308033053/85/Exact-Algorithms-for-Minimum-Edge-Dominating-Set-and-Lowest-Edge-Dominating-Set-8-320.jpg)
![NP-Hard Problems for EDS
Previous Time BoundsMinimum EDS
Input: An -vertex graph
Output: A minimum EDS of [Xiao & Nagamochi 2012]
Parameterized EDS
Input: An -vertex graph & an integer
Output: Does have an EDS of size ?
· Fast for small
[Iwaide & Nagamochi 2015]
How fast can solve?
7](https://image.slidesharecdn.com/2016a-160308033053/85/Exact-Algorithms-for-Minimum-Edge-Dominating-Set-and-Lowest-Edge-Dominating-Set-9-320.jpg)
![NP-Hard Problems for EDS
Previous Time BoundsMinimum EDS
Input: An -vertex graph
Output: A minimum EDS of [Xiao & Nagamochi 2012]
Parameterized EDS
Input: An -vertex graph & an integer
Output: Does have an EDS of size ?
· Fast for small
[Iwaide & Nagamochi 2015]
How fast can solve?
Our Purpose
· Design an algorithm solving both problems with currently best time
? time & time 8](https://image.slidesharecdn.com/2016a-160308033053/85/Exact-Algorithms-for-Minimum-Edge-Dominating-Set-and-Lowest-Edge-Dominating-Set-10-320.jpg)


![Lowest Solution
Vertex Cover (VC) and Maximum Matching (MM)
Note: MM can be found
in polynomial time
VC MM
· To find a minimum VC NP-hard
· VC with VC MM ? in polynomial time [Gavril 1977]
Lowest case is easy for some NP-hard problem
11](https://image.slidesharecdn.com/2016a-160308033053/85/Exact-Algorithms-for-Minimum-Edge-Dominating-Set-and-Lowest-Edge-Dominating-Set-13-320.jpg)




![Minimum EDS by PEDS Algorithm
· Minimum Independent EDS Minimum EDS
[Yannakakis & Gavril 1980]
: minimum size of EDS of
found by a PEDS algorithm in poly. time
Case 1.
minimum EDS that contains
Case 2.
minimum EDS that contains
16](https://image.slidesharecdn.com/2016a-160308033053/85/Exact-Algorithms-for-Minimum-Edge-Dominating-Set-and-Lowest-Edge-Dominating-Set-18-320.jpg)
![NP-Completeness of Lowest EDS
1-In-3 3SAT NP-hard [Garey & Johnson 1979]
Input: A set of variables & a set of clauses on s.t. each
clause has exactly three literals
Output: assignment on s.t. each clause has exactly one
true literal?
· Polynomial-time reduction to Lowest EDS
17](https://image.slidesharecdn.com/2016a-160308033053/85/Exact-Algorithms-for-Minimum-Edge-Dominating-Set-and-Lowest-Edge-Dominating-Set-19-320.jpg)
![Application
· Evaluating the worst-case performance of trunking
Switch
Shared lines
Nodes
Occupied / Vacant lines
Bipartite graph
· Line is busy Occupied lines become a maximal matching of
· Minimum maximal matching Minimum EDS
[Yannakakis & Gavril 1980]
18](https://image.slidesharecdn.com/2016a-160308033053/85/Exact-Algorithms-for-Minimum-Edge-Dominating-Set-and-Lowest-Edge-Dominating-Set-20-320.jpg)