Feature and Variable Selection in Classification
- 1. Feature and Variable Selection in Classification Aaron Karper University of Bern Aaron Karper (UniBe) Feature selection 1 / 12
- 2. Why? Why not use all the features? training error test error Interpretability error Overfitting Computational Complexity Model complexity Aaron Karper (UniBe) Feature selection 2 / 12
- 3. What are the options? Ranking Measure relevance for each feature separately. The good: The bad: Xor problem. Fast Aaron Karper (UniBe) Feature selection 3 / 12
- 4. What are the options? Ranking Measure relevance for each feature separately. The good: The bad: Xor problem. Fast Aaron Karper (UniBe) Feature selection 3 / 12
- 5. What are the options? Xor problem Aaron Karper (UniBe) Feature selection 4 / 12
- 6. What are the options? Filters Walk in feature subset space evaluate proxy measure train classifier The bad: The good: Suboptimal performance Flexibility Aaron Karper (UniBe) Feature selection 5 / 12
- 7. What are the options? Wrappers Walk in feature subset space The good: train classifier The bad: Slow training Accuracy Aaron Karper (UniBe) Feature selection 6 / 12
- 8. What are the options? Embedded methods Integrate feature selection into classifier. The good: The bad: Accuracy, training time Aaron Karper (UniBe) Feature selection Lacks flexibility 7 / 12
- 9. What should I use? What is the best one? Accuracy-wise: embedded or wrapper. Complexity-wise: ranking, filters. Why not both? Aaron Karper (UniBe) Feature selection 8 / 12
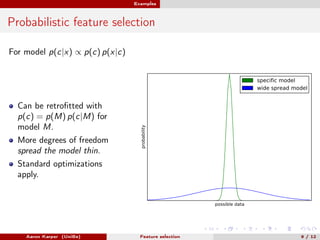
- 10. Examples Probabilistic feature selection For model p(c|x) ∝ p(c) p(x|c) Can be retrofitted with p(c) = p(M) p(c|M) for model M. More degrees of freedom spread the model thin. probability specific model wide spread model Standard optimizations apply. possible data Aaron Karper (UniBe) Feature selection 9 / 12
- 11. Examples Probabilistic feature selection For model p(c|x) ∝ p(c) p(x|c) Can be retrofitted with p(c) = p(M) p(c|M) for model M. More degrees of freedom spread the model thin. probability specific model wide spread model Standard optimizations apply. possible data Aaron Karper (UniBe) Feature selection 9 / 12
- 12. Examples Probabilistic feature selection Akaike information criterion every additional variable needs to explain e times as much data. Bayesian information criterion Unused parameters are marginalized. Minimum descriptor length Aaron Karper (UniBe) Feature selection 10 / 12
- 13. Examples Autoencoder Reconstruction 2000 1000 500 Deep neural network. Create fixed size information bottleneck. Bottleneck Train to being able to reconstruct original data. 30 500 1000 2000 Input Aaron Karper (UniBe) Feature selection 11 / 12
- 14. Prediction Predictions Embedded methods will improve more than other approaches. Others as first step for complexity reasons. Aaron Karper (UniBe) Feature selection 12 / 12