![環境の状態 s の?損された観測 o (死?，記憶?如，マルチエージェント
性等が原因)＝ 不完全知覚問題 (Partially Observabl MDP, POMDP)
例 : Montezuma?s Revenge
不完全知覚
Copyright (C) DeNA Co.,Ltd. All Rights Reserved.
3
鍵を獲得した等 “他の部屋で何をやったか” を覚えていないと不完全知覚
→ 現実環境ではエージェントが得られる情報などたかが知れている
※ [Bellmare et al., 2012]](https://image.slidesharecdn.com/abstfuncopy-170724030609/85/FeUdal-Networks-for-Hierarchical-Reinforcement-Learning-3-320.jpg)
![不完全知覚への対処
Copyright (C) DeNA Co.,Ltd. All Rights Reserved.
6
階層型強化学習
機能 :
? 意思決定を上位層と下位層に分割する (後述)
? 観測に対する MDP で事?りる部分 (サブタスク) を下位層が担当
? サブタスクの選択，遷移順を決める上位層が担当
? ?順，記憶を上位層が?的意識 (の遷移) として扱い状態を分離
? 下位層の?動 (サブタスク適応) が使い回せるので汎化性能が?い
問題点 :
? ?律的なサブタスク分割が?常に困難
→ FeUdal Networks [Vezhnevets et al., 2017]というサブタスク分解を
End-to-End で?うアーキテクチャを DeepMind が考案](https://image.slidesharecdn.com/abstfuncopy-170724030609/85/FeUdal-Networks-for-Hierarchical-Reinforcement-Learning-6-320.jpg)
![不完全知覚への対処 (再掲)
Copyright (C) DeNA Co.,Ltd. All Rights Reserved.
10
階層型強化学習
機能 :
? 意思決定を上位層と下位層に分割する (後述)
? 観測に対する MDP で事?りる部分 (サブタスク) を下位層が担当
? サブタスクの選択，遷移順を決める上位層が担当
? ?順，記憶を上位層が?的意識 (の遷移) として扱い状態を分離
? 下位層の?動 (サブタスク適応) が使い回せるので汎化性能が?い
問題点 :
? ?律的なサブタスク分割が?常に困難
→ FeUdal Networks [Vezhnevets et al., 2017] というサブタスク分解を
End-to-End で?うアーキテクチャを DeepMind が考案](https://image.slidesharecdn.com/abstfuncopy-170724030609/85/FeUdal-Networks-for-Hierarchical-Reinforcement-Learning-10-320.jpg)
![Feudal reinforcement learning, FRL [Dayan and Hinton, 1993]
? 意思決定を上位層と下位層に分割する
? 下位意思決定者 Sub-Maneer, 上位意思決定者 Manager という
概念を提供
? FuNs (本題) のアイディア元
? Sutton の強化学習本よりも前なので概念的なものに近い？
FeUdal Networks - 背景概念
Copyright (C) DeNA Co.,Ltd. All Rights Reserved.
11](https://image.slidesharecdn.com/abstfuncopy-170724030609/85/FeUdal-Networks-for-Hierarchical-Reinforcement-Learning-11-320.jpg)
![Option [Sutton et al., 1999]
? ?期的な?動?策 Option (通常の?策概念に goal 状態 =
termination condition を加えたもの) とその Option そのものを選
択する policy-over-option を導?
? Semi-MDP への対処が主眼 (意思決定が疎)
? 個別の Option の?律的な学習は不?分な側?がある
? ?較的古典的な話
Option-Critic [Bacon et al., 2017]
? Option を Deep RL 化したもの (Goal 概念が薄い？)
? End-to-End で学習可能
? 上位?策と下位?策の役割が未分化する問題点が存在
FeUdal Networks - 背景概念
Copyright (C) DeNA Co.,Ltd. All Rights Reserved.
12](https://image.slidesharecdn.com/abstfuncopy-170724030609/85/FeUdal-Networks-for-Hierarchical-Reinforcement-Learning-12-320.jpg)
![FRL の意思決定を上位層と下位層に分割が根幹アイディア
? 下位意思決定者 Worker (FRL での sub-maneer)
? 上位意思決定者 Manager
FeUdal Networks - 概要
Copyright (C) DeNA Co.,Ltd. All Rights Reserved.
13
↑ 下位の?動 primitive-policy を選択する Worker
CNN 部で
観測 x を変換????
↓
A3C で学習
↓
← サブゴール
↓ 上位の?動 sub-policy を選択する Manager
※ [Vezhnevets et al., 2017]](https://image.slidesharecdn.com/abstfuncopy-170724030609/85/FeUdal-Networks-for-Hierarchical-Reinforcement-Learning-13-320.jpg)
![Manager (上位層)訓練のための遷移?策勾配 :
Worker (下位層)とは異なる勾配を定義
Transition policy gradient for the Manager
Copyright (C) DeNA Co.,Ltd. All Rights Reserved.
16
※
※
↑
Manager から与えられる仮想的な収益
※ Option-Critic は下位層の意思決定者からの勾配を使って学習
※ [Vezhnevets et al., 2017]](https://image.slidesharecdn.com/abstfuncopy-170724030609/85/FeUdal-Networks-for-Hierarchical-Reinforcement-Learning-16-320.jpg)
![結果 - Montezuma?s Revenge
Copyright (C) DeNA Co.,Ltd. All Rights Reserved.
20
↓ 以前の時系列出?にとって goal になってる数
← 素の LSTM より良い
200 epoch 未満で最初の部屋を突破
(1 epoch = 100万 step )
※ [Vezhnevets et al., 2017]](https://image.slidesharecdn.com/abstfuncopy-170724030609/85/FeUdal-Networks-for-Hierarchical-Reinforcement-Learning-20-320.jpg)
![結果 - サブ?策の確認
Copyright (C) DeNA Co.,Ltd. All Rights Reserved.
21
ゴール固定時の動き :
Manager がゲーム中経験したサブゴール g を記憶しておき，あえて固定
して?動させる事でサブ?策の動きを確認できる
上記グラデーションマップは Agent の空間滞在?率を平均化したもの
→ 異なる動きが確認できる
例 : sub-policy 3 は空気を補充している
※ [Vezhnevets et al., 2017]](https://image.slidesharecdn.com/abstfuncopy-170724030609/85/FeUdal-Networks-for-Hierarchical-Reinforcement-Learning-21-320.jpg)
![結果 - Option-Critic との?較
Copyright (C) DeNA Co.,Ltd. All Rights Reserved.
22
FuNs : Option-Critic :
同じ End-to-End な階層型強化学習 Option-Critic と?較して良い成績
停滞気味の Option-Critic に?べて，FuN は更に上がり続けている
※ [Vezhnevets et al., 2017]](https://image.slidesharecdn.com/abstfuncopy-170724030609/85/FeUdal-Networks-for-Hierarchical-Reinforcement-Learning-22-320.jpg)
![結果 - アイディアの正しさ
Copyright (C) DeNA Co.,Ltd. All Rights Reserved.
23
4種の?損型 FuN との?較:
Non feudal FuN : ?策勾配で訓練，内部報酬も使わない (Option-Criticに近い)
Pure feudal FuN : Worker に内部報酬を使わない
Manager via PG FuN : Manager を?策勾配で訓練
Absolute goals Fun : 絶対ゴールを使? (具体的な定義は読みきれなかった)
→ 全てにおいて FuN が勝利 = 3つのアイディアの有効性
※ [Vezhnevets et al., 2017]](https://image.slidesharecdn.com/abstfuncopy-170724030609/85/FeUdal-Networks-for-Hierarchical-Reinforcement-Learning-23-320.jpg)
![結果 - アイディアの正しさ
Copyright (C) DeNA Co.,Ltd. All Rights Reserved.
24
Dilated LSTM に関する?較:
No dilation : Manager に通常 LSTM を使?
Manager horizon = 1 : c = 1 で Manager と Dilated LSTM を運?
→ 全てにおいて FuN が勝利 = Dilated LSTM の有効性
c = 1 でも上がってはいる
※ [Vezhnevets et al., 2017]](https://image.slidesharecdn.com/abstfuncopy-170724030609/85/FeUdal-Networks-for-Hierarchical-Reinforcement-Learning-24-320.jpg)
![結果 - アイディアの正しさ
Copyright (C) DeNA Co.,Ltd. All Rights Reserved.
25
Dilated LSTM に関する?較:
dLSTM : FuN ではなく通常の A3C にDilated LSTMのみを使?
→ 基本的には FuN と 通常LSTM が勝利
= Dilated LSTM は Manager レベルだから有効
※ [Vezhnevets et al., 2017]](https://image.slidesharecdn.com/abstfuncopy-170724030609/85/FeUdal-Networks-for-Hierarchical-Reinforcement-Learning-25-320.jpg)
![結果 - 転移への試み
Copyright (C) DeNA Co.,Ltd. All Rights Reserved.
26
Action repeat of 4 から Action repeat 無しへの重み転
?定フレーム数 (論?中では 4 frame) の間同じ?動をする通常のやり?
で学習した重みを，1 frame ごとに?動を意思決定するタスクに転?
その学習しないでの成績 (流?に各時間関係パラメータは 4 倍にする)
→ FuN の?い成績は Manager で学習した上位?策の有?性を意味する
→ 同?タスクだと Maneger の汎?性の?さの証明にはならない気も？
※ [Vezhnevets et al., 2017]](https://image.slidesharecdn.com/abstfuncopy-170724030609/85/FeUdal-Networks-for-Hierarchical-Reinforcement-Learning-26-320.jpg)
![感想
Copyright (C) DeNA Co.,Ltd. All Rights Reserved.
27
End-to-End なサブゴール形成
? 絶対的ではなく相対的なゴール定義 (ある種の未来?向予測) という
アイディアで成したのは興味深い
? 固定?時間 c step を可変?にできるとなお良い
? ?い時間?でゴールを定義したい場合への対処を考えて
? ?的論的には Option の?がサブゴールと?える
※ [Vezhnevets et al., 2017]](https://image.slidesharecdn.com/abstfuncopy-170724030609/85/FeUdal-Networks-for-Hierarchical-Reinforcement-Learning-27-320.jpg)
![引??献 (スライド中)
Copyright (C) DeNA Co.,Ltd. All Rights Reserved.
29
[Vezhnevets et al., 2017] Vezhnevets, A. S., Osindero, S., Schaul, T., Heess, N., Jaderberg, M., Silver, D., and
Kavukcuoglu, K. FeUdal Networks for Hierarchical Reinforcement Learning. ArXiv. Retrieved from http://
arxiv.org/abs/1703.01161 (2017).
[Bellmare et al., 2012] Bellemare, M. G., Naddaf, Y., Veness, J., and Bowling, M. The arcade learning
environment: An evaluation platform for general agents. Journal of Artificial Intelligence Research. (2012).
[Dayan and Hinton, 1993] Dayan, P., and Hinton, G. E. Feudal reinforcement learning. In NIPS . Morgan
Kaufmann Publishers. (1993).
[Sutton et al., 1999] Sutton, R. S., Precup, D., and Singh, S. Between mdps and semi-mdps: A framework for
temporal abstraction in reinforcement learning. Artificial intelligence. (1999).
[Bacon et al., 2017] Bacon, P. L., Precup, D., and Harb, J. The option-critic architecture. In AAAI. (2017).
[Von Mises–Fisher distribution] https://en.wikipedia.org/wiki/Von_Mises-Fisher_distribution](https://image.slidesharecdn.com/abstfuncopy-170724030609/85/FeUdal-Networks-for-Hierarchical-Reinforcement-Learning-29-320.jpg)
![結果 - オマケ
Copyright (C) DeNA Co.,Ltd. All Rights Reserved.
30
Water maze で実際に獲得された?動 :
Staet (緑)位置からの?動以外，同じ半径で回転して探索するサブ?策が
学習される
右端は goal をランダムに設定，200step 固定して学習して得られたサ
ブ?策ケース
※ [Vezhnevets et al., 2017]](https://image.slidesharecdn.com/abstfuncopy-170724030609/85/FeUdal-Networks-for-Hierarchical-Reinforcement-Learning-30-320.jpg)
FeUdal Networks for Hierarchical Reinforcement Learning
- 1. Copyright (C) DeNA Co.,Ltd. All Rights Reserved. DeNA Co., Ltd. AIシステム部 AI 研究開発グループ 甲野 佑 FeUdal Networks for Hierarchical Reinforcement Learning
- 2. 甲野 佑 所属 : 株式会社ディー?エヌ?エー AI システム部 AI 研究開発グルー プ 出? : 東京電機?学 (学部?博?) = おたく?学 研究 : 強化学習 ＋ 脳神経?認知 → ゲーム AI 開発 (DeNA) ? 認知や脳神経と機械学習を組み合わせて純粋な理学研究より実?的な 強化学習アルゴリズムを構築したい ? ?間の柔軟性→不完全知覚(への対処)→限定合理性→汎?性＝階層性？ ??紹介 Copyright (C) DeNA Co.,Ltd. All Rights Reserved. 2
- 3. 環境の状態 s の?損された観測 o (死?，記憶?如，マルチエージェント 性等が原因)＝ 不完全知覚問題 (Partially Observabl MDP, POMDP) 例 : Montezuma?s Revenge 不完全知覚 Copyright (C) DeNA Co.,Ltd. All Rights Reserved. 3 鍵を獲得した等 “他の部屋で何をやったか” を覚えていないと不完全知覚 → 現実環境ではエージェントが得られる情報などたかが知れている ※ [Bellmare et al., 2012]
- 4. 状態 b ?動2状態 a?動 1 観測状態? 不完全知覚への問題 Copyright (C) DeNA Co.,Ltd. All Rights Reserved. 4 POMDP が困難な理由の?つは観測に対する真の状態の混同 → ?動の選択確率 π は観測状態に対し?意しか持てない事 状態 b ?動2状態 a?動 1 観測状態? 本来左に?くべき状態 a 本来右に?くべき状態 b → 何らかの?法で分離してやれば良い
- 5. 完全記憶 機能 : ? 初期状態から全ての状態遷移を記憶する事で “本来異なる状態” を分離 問題点 : ? 全ての履歴を覚えているのは現実的に不可能 ? 死?や他エージェントの内部状態はどちらにせよ問題 ? LSTM 等を使っても問題が解決するわけじゃない ? 真??にやると状態数が容易に爆発する (かつ汎化されない) ? 状態概念が複雑になり報酬などの獲得情報が環境全体に対してスパー スになりやすい (強化学習全般の問題を加速させる) 不完全知覚への対処 Copyright (C) DeNA Co.,Ltd. All Rights Reserved. 5
- 6. 不完全知覚への対処 Copyright (C) DeNA Co.,Ltd. All Rights Reserved. 6 階層型強化学習 機能 : ? 意思決定を上位層と下位層に分割する (後述) ? 観測に対する MDP で事?りる部分 (サブタスク) を下位層が担当 ? サブタスクの選択，遷移順を決める上位層が担当 ? ?順，記憶を上位層が?的意識 (の遷移) として扱い状態を分離 ? 下位層の?動 (サブタスク適応) が使い回せるので汎化性能が?い 問題点 : ? ?律的なサブタスク分割が?常に困難 → FeUdal Networks [Vezhnevets et al., 2017]というサブタスク分解を End-to-End で?うアーキテクチャを DeepMind が考案
- 7. 本題 : FeUdal Networks (FuN) の前に 階層型強化学習のイメージを少し 階層型強化学習 Copyright (C) DeNA Co.,Ltd. All Rights Reserved. 7
- 8. 通常(?階層型)の強化学習イメージ Copyright (C) DeNA Co.,Ltd. All Rights Reserved. 8 細かな意思決定 プリミティブな?動 : a ?策 : π(a;s)
- 9. 階層型強化学習イメージ Copyright (C) DeNA Co.,Ltd. All Rights Reserved. 9 細かな意思決定 プリミティブな?動 : a ?まかな意思決定 ?的指向 : g 下位層?策 : π(a;s,g) 上位層?策 : πgoal(g;s) 下位層?策 を選択 (g として) × 複数 試?錯誤か ら上位層? 策を?成？
- 10. 不完全知覚への対処 (再掲) Copyright (C) DeNA Co.,Ltd. All Rights Reserved. 10 階層型強化学習 機能 : ? 意思決定を上位層と下位層に分割する (後述) ? 観測に対する MDP で事?りる部分 (サブタスク) を下位層が担当 ? サブタスクの選択，遷移順を決める上位層が担当 ? ?順，記憶を上位層が?的意識 (の遷移) として扱い状態を分離 ? 下位層の?動 (サブタスク適応) が使い回せるので汎化性能が?い 問題点 : ? ?律的なサブタスク分割が?常に困難 → FeUdal Networks [Vezhnevets et al., 2017] というサブタスク分解を End-to-End で?うアーキテクチャを DeepMind が考案
- 11. Feudal reinforcement learning, FRL [Dayan and Hinton, 1993] ? 意思決定を上位層と下位層に分割する ? 下位意思決定者 Sub-Maneer, 上位意思決定者 Manager という 概念を提供 ? FuNs (本題) のアイディア元 ? Sutton の強化学習本よりも前なので概念的なものに近い？ FeUdal Networks - 背景概念 Copyright (C) DeNA Co.,Ltd. All Rights Reserved. 11
- 12. Option [Sutton et al., 1999] ? ?期的な?動?策 Option (通常の?策概念に goal 状態 = termination condition を加えたもの) とその Option そのものを選 択する policy-over-option を導? ? Semi-MDP への対処が主眼 (意思決定が疎) ? 個別の Option の?律的な学習は不?分な側?がある ? ?較的古典的な話 Option-Critic [Bacon et al., 2017] ? Option を Deep RL 化したもの (Goal 概念が薄い？) ? End-to-End で学習可能 ? 上位?策と下位?策の役割が未分化する問題点が存在 FeUdal Networks - 背景概念 Copyright (C) DeNA Co.,Ltd. All Rights Reserved. 12
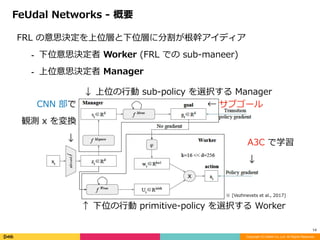
- 13. FRL の意思決定を上位層と下位層に分割が根幹アイディア ? 下位意思決定者 Worker (FRL での sub-maneer) ? 上位意思決定者 Manager FeUdal Networks - 概要 Copyright (C) DeNA Co.,Ltd. All Rights Reserved. 13 ↑ 下位の?動 primitive-policy を選択する Worker CNN 部で 観測 x を変換???? ↓ A3C で学習 ↓ ← サブゴール ↓ 上位の?動 sub-policy を選択する Manager ※ [Vezhnevets et al., 2017]
- 14. FuN はアーキテクチャ全域で微分可能 ＝ Manager によるサブタスク分 割を End-to-End で学習可能 類似概念 Option と FuN の?きな違いは Goal 概念があるか否か - Option は Goal に到達したら上位?策によって次の Goal を決定 - FuN は定数時間 c step によって意思決定タイミングを区切る - この定数時間 c step の割り切りが秘訣の?つ？ - 論?中の結果は c = 10 FeUdal Networks - 概要 Copyright (C) DeNA Co.,Ltd. All Rights Reserved. 14
- 15. FuNs の特徴 1. Transition policy gradient for training the Manager ? Manager 訓練のための遷移?策勾配 (遷移?策＝上位層?策) 2. Relative rather than absolute goals ? 絶対的ではなく相対的な定義によるサブゴール形成 ? 獲得された潜在状態ベクトル s に対する差分を g として学習 3. Lower temporal resolution for Manager ? Manager の扱う時間間隔の低解像度化 ? 意思決定タイミングと Dilated LSTM 4. Intrinsic motivation for the Worker ? 内部報酬(といっても?較的弱め) FeUdal Networks - 特徴 Copyright (C) DeNA Co.,Ltd. All Rights Reserved. 15
- 16. Manager (上位層)訓練のための遷移?策勾配 : Worker (下位層)とは異なる勾配を定義 Transition policy gradient for the Manager Copyright (C) DeNA Co.,Ltd. All Rights Reserved. 16 ※ ※ ↑ Manager から与えられる仮想的な収益 ※ Option-Critic は下位層の意思決定者からの勾配を使って学習 ※ [Vezhnevets et al., 2017]
- 17. 絶対ではなく相対的なサブゴール : = Von Mises–Fisher 分布 (d 次元の?向の正規分布) を近似 Relative rather than absolute goals Copyright (C) DeNA Co.,Ltd. All Rights Reserved. 17 実際の相対的ゴールの更新式： ↓ 意味的には： ↑ Von Mises–Fisher 分布 ※ https://en.wikipedia.org/wiki/Von_Mises-Fisher_distribution Cos 類似度との比例関係：
- 18. Manager が扱う時間間隔の低解像度化 Dilated LSTM : Lower temporal resolution for Manager Copyright (C) DeNA Co.,Ltd. All Rights Reserved. 18 r (= c ; 論?中) 系列数の LSTM を?意し，r サイクル毎に新たな 状態を保存していく → Manager レベルでは?期の記憶を保持 (r step 間隔)
- 19. 内部報酬 : Intrinsic motivation for the Worker Copyright (C) DeNA Co.,Ltd. All Rights Reserved. 19 流?りの好奇? (intrinsic reword) とはまた異なる 環境探索効果は少ないので好奇?との組み合わせは可能 ↑ 予測されたゴールとの類似度 ※ 0 ~ c step の間に goal に近づけば OK !
- 20. 結果 - Montezuma?s Revenge Copyright (C) DeNA Co.,Ltd. All Rights Reserved. 20 ↓ 以前の時系列出?にとって goal になってる数 ← 素の LSTM より良い 200 epoch 未満で最初の部屋を突破 (1 epoch = 100万 step ) ※ [Vezhnevets et al., 2017]
- 21. 結果 - サブ?策の確認 Copyright (C) DeNA Co.,Ltd. All Rights Reserved. 21 ゴール固定時の動き : Manager がゲーム中経験したサブゴール g を記憶しておき，あえて固定 して?動させる事でサブ?策の動きを確認できる 上記グラデーションマップは Agent の空間滞在?率を平均化したもの → 異なる動きが確認できる 例 : sub-policy 3 は空気を補充している ※ [Vezhnevets et al., 2017]
- 22. 結果 - Option-Critic との?較 Copyright (C) DeNA Co.,Ltd. All Rights Reserved. 22 FuNs : Option-Critic : 同じ End-to-End な階層型強化学習 Option-Critic と?較して良い成績 停滞気味の Option-Critic に?べて，FuN は更に上がり続けている ※ [Vezhnevets et al., 2017]
- 23. 結果 - アイディアの正しさ Copyright (C) DeNA Co.,Ltd. All Rights Reserved. 23 4種の?損型 FuN との?較: Non feudal FuN : ?策勾配で訓練，内部報酬も使わない (Option-Criticに近い) Pure feudal FuN : Worker に内部報酬を使わない Manager via PG FuN : Manager を?策勾配で訓練 Absolute goals Fun : 絶対ゴールを使? (具体的な定義は読みきれなかった) → 全てにおいて FuN が勝利 = 3つのアイディアの有効性 ※ [Vezhnevets et al., 2017]
- 24. 結果 - アイディアの正しさ Copyright (C) DeNA Co.,Ltd. All Rights Reserved. 24 Dilated LSTM に関する?較: No dilation : Manager に通常 LSTM を使? Manager horizon = 1 : c = 1 で Manager と Dilated LSTM を運? → 全てにおいて FuN が勝利 = Dilated LSTM の有効性 c = 1 でも上がってはいる ※ [Vezhnevets et al., 2017]
- 25. 結果 - アイディアの正しさ Copyright (C) DeNA Co.,Ltd. All Rights Reserved. 25 Dilated LSTM に関する?較: dLSTM : FuN ではなく通常の A3C にDilated LSTMのみを使? → 基本的には FuN と 通常LSTM が勝利 = Dilated LSTM は Manager レベルだから有効 ※ [Vezhnevets et al., 2017]
- 26. 結果 - 転移への試み Copyright (C) DeNA Co.,Ltd. All Rights Reserved. 26 Action repeat of 4 から Action repeat 無しへの重み転 ?定フレーム数 (論?中では 4 frame) の間同じ?動をする通常のやり? で学習した重みを，1 frame ごとに?動を意思決定するタスクに転? その学習しないでの成績 (流?に各時間関係パラメータは 4 倍にする) → FuN の?い成績は Manager で学習した上位?策の有?性を意味する → 同?タスクだと Maneger の汎?性の?さの証明にはならない気も？ ※ [Vezhnevets et al., 2017]
- 27. 感想 Copyright (C) DeNA Co.,Ltd. All Rights Reserved. 27 End-to-End なサブゴール形成 ? 絶対的ではなく相対的なゴール定義 (ある種の未来?向予測) という アイディアで成したのは興味深い ? 固定?時間 c step を可変?にできるとなお良い ? ?い時間?でゴールを定義したい場合への対処を考えて ? ?的論的には Option の?がサブゴールと?える ※ [Vezhnevets et al., 2017]
- 28. 感想 Copyright (C) DeNA Co.,Ltd. All Rights Reserved. 28 LSTM への依存性 ? 不完全情報への対処は所詮 LSTM まかせ ? 成績で Option-Critic に優っているのは A3C や LSTM のおかげ ? 固定? c step サイクルの Dilated LSTM が有効だった？ ? FuNs ?体が Dilated LSTM を使うための構造とも捉えられる ? ?期的な Dilated LSTM といっても限界が存在するはず → より圧縮(記号化)された記憶表現を End-to-End で学習すべき？
- 29. 引??献 (スライド中) Copyright (C) DeNA Co.,Ltd. All Rights Reserved. 29 [Vezhnevets et al., 2017] Vezhnevets, A. S., Osindero, S., Schaul, T., Heess, N., Jaderberg, M., Silver, D., and Kavukcuoglu, K. FeUdal Networks for Hierarchical Reinforcement Learning. ArXiv. Retrieved from http:// arxiv.org/abs/1703.01161 (2017). [Bellmare et al., 2012] Bellemare, M. G., Naddaf, Y., Veness, J., and Bowling, M. The arcade learning environment: An evaluation platform for general agents. Journal of Artificial Intelligence Research. (2012). [Dayan and Hinton, 1993] Dayan, P., and Hinton, G. E. Feudal reinforcement learning. In NIPS . Morgan Kaufmann Publishers. (1993). [Sutton et al., 1999] Sutton, R. S., Precup, D., and Singh, S. Between mdps and semi-mdps: A framework for temporal abstraction in reinforcement learning. Artificial intelligence. (1999). [Bacon et al., 2017] Bacon, P. L., Precup, D., and Harb, J. The option-critic architecture. In AAAI. (2017). [Von Mises–Fisher distribution] https://en.wikipedia.org/wiki/Von_Mises-Fisher_distribution
- 30. 結果 - オマケ Copyright (C) DeNA Co.,Ltd. All Rights Reserved. 30 Water maze で実際に獲得された?動 : Staet (緑)位置からの?動以外，同じ半径で回転して探索するサブ?策が 学習される 右端は goal をランダムに設定，200step 固定して学習して得られたサ ブ?策ケース ※ [Vezhnevets et al., 2017]