Fibonacci en
- 1. MATHEMATICS DOES NOT KNOW THE BORDERS
- 3. Leonardo Fibonacci An Italian mathematician, born around 1170 in Pisa. He contributed to the revival of classical exact sciences after their decline in the early Middle ages. Fibonacci travelled in the Mediterranean region in order to get educated by the leading mathematicians of the time.
- 4. Works Fibonacci remains in the history of science mainly with his âGeometric practiceâ deals with geometry and trigonometry and âBook about squaresâ â with algebra. The book âFlosâ contains solutions of problems described earlier by Joan from Palermo. Today we also know about a few other works of his, which havenât been preserved. âBook of calculationâ.
- 5. Contribution to mathematics Fibonacci is famous for introducing Arabic numbers in Europe, which he used in his âBook of calculationâ. 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 During his travels in the Mediterranean region he discovered a problem about a number sequence with interesting properties, which was later named after him by the French mathematician Luka.
- 6. The problem about a population of rabbits Fibonacci presents the sequence through a problem involving reproduction of rabbits. They put a pair of rabbits in a place, surrounded with walls, so as to see how many pairs of rabbits will be born in a year. According to the nature of rabbits a pair of rabbits will reproduce another pair in one month and rabbits will be able to bear other rabbits from the second month after they were born.
- 7. The problem about a population of rabbits Ð month one pair of newborn ÐÐ month one pair (they donât reproduce) ÐÐÐ month 1 + 1 = 2 pairs ÐV month 2 + 1= 3 pairs (only one pair reproduces) V month 3 + 2 = 5 pairs
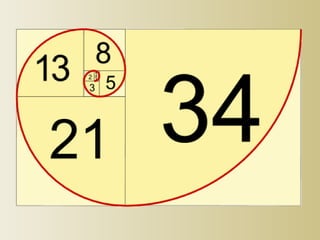
- 8. Fibonacci sequence In the sequence of numbers each number is the sum of the previous two numbers: F1 = 1, F2 = 1, F3 = F1+ F2 = 1 + 1 = 2, F4 = F2 + F3 = 1 + 2 = 3, F5 = 5, F6 = 8, F7 = 13, F8 = 21 ,etc: Fn=Fn-1+Fn-2, for all n>2 .
- 9. Characteristics of the sequence Each number in the sequence divided by the previous one gives approximately 1.618. This number is called Fibonacci constant and its symbol is the Greek letter Ï. There is a difference only for the first few members of the sequence. An interesting fact is that the quotient of each number in the sequence and the number that follows it is presented by this formula: 11618.1618.01 â=â==â Ï i i F F 618.1 1 == âi i F F Ï
- 10. The number Ï The number Ï was used in ancient Egypt and it was known under various names: Golden ratio, Golden number, Heavenly proportion and many others. 50 years ago, the mathematician Mark Barr suggested that this ratio be noted with the Greek letter Ï. It is the first letter of the name of the great ancient Greek sculptor Phidias, who according to the legend often used the Golden ratio in his statues.
- 11. Golden ratio The number Ï = 1.618 known also as âGolden ratioâ is a relationship of parts in which the larger part relates to the smaller one, as the sum of the parts to the larger part and each relationship equals Ï. a : b = Ï (a + b) : а = Ï a : b = (a + b) : а a b a + b
- 12. Illustration of the sequence We can illustrate the Fibonacci sequence with a row of rectangles: The first two members of this row are squares with a side 1. Then there is a rectangle with sides 1 and 2, made up of two squares. We add a new square with a side 2 (which is equal to the larger side of the rectangle) and we make a rectangle with sides 2 and 3, etc.
- 14. In the ancient times The Golden ratio was known in the remote past. The sequence 3, 5, 8, 13, 18, 21 is represented in the sunbeams in a drawing in the Magura cave in the Northwestern Bulgaria (10000 B.C.) The Golden ratio was encoded in small standards of measures which have been found in the necropolis in Varna, Bulgaria (5000 B.C.).
- 15. Harmony In the past, architects, painters and theorists often considered the Golden ratio to be an ideal expression of beauty. We find it in lots of buildings and sculptures: The Egyptian pyramids, the Parthenon in Athens, the Gothic cathedrals in Western Europe.
- 16. During the Renaissance The book âDivine Proportionâ by the monk Luca Paccoli was published in 1509. The illustrations in it are supposed to have been done by Leonardo da Vinci. Scientistsâ and artistsâ interest towards the Golden ratio increased and it found application in geometry, art and architecture. The symbol of Renaissance is Leonardoâs Vitruvian Man. The picture and the text are often called the Canon of proportions.
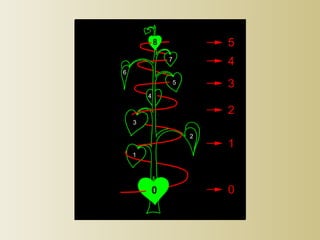
- 17. The Golden ratio in nature In 1754 Charles Bonnet discovered that if the places where the leaves âattachâ to the branch are connected mentally, the result will be a few spirals, the so called The spaces between the cycles of the leaves are proportional to the Fibonacci numbers. a : b = b : c â 1.6 genetic screw.
- 20. The Golden ratio in nature Sunflowers, with their spirals of seeds, have the ratio 1.618 between the diametres of each rotation. This coefficient is also observed in the relations between various nature components.
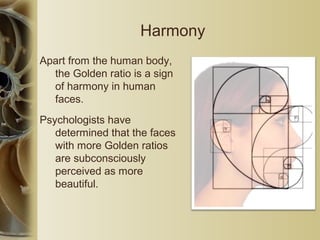
- 21. Harmony Apart from the human body, the Golden ratio is a sign of harmony in human faces. Psychologists have determined that the faces with more Golden ratios are subconsciously perceived as more beautiful.
- 23. ââAcademic Ivan TsenovâAcademic Ivan Tsenovâ Secondary School of MathematicsSecondary School of Mathematics and Natural Sciencesand Natural Sciences Bulgaria, VratsaBulgaria, Vratsa