finite automata
- 1. STRING MATCHING WITH FINITE AUTOMATA Prepared By: Sabiya Fatima Email ID: sabiya1990fatima@gmail.com 1
- 2. Contents 1. STRING MATCHING 2. FINITE AUTOMATA 3. FINITE STATE MACHINE 4. STRING MATCHING WITH FINITE AUTOMATA 5. STRING MATCHING AUTOMATA 6. FINITE AUTOMATON MATCHER 7. COMPUTING THE TRANSITION FUNCTION 8. RUNNING TIME 2
- 3. 3
- 4. STRING MATCHING: In General, Whenever you use a search engine, or a âfindâ function like grep, you are utilizing a string matching program. Many of these programs create finite automata in order to effectively search for your string. OR The Objective of string matching is to find the location of specific text pattern within larger body of text.(a sentence, a paragraph , a book etc..) 4
- 5. 5
- 6. 6
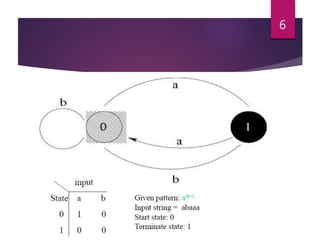
- 7. FINITE STATE MACHINE ïĩ A finite state machine (FSM, also known as a deterministic finite automaton or DFA) is a way of representing a language. ïĩ we represent the language as the set of those strings accepted by some program. So, once you've found the right machine, we can test whether a given string matches just by running it. 7
- 8. 8
- 9. 9
- 10. 10
- 11. 11
- 12. 12 m+1 |â| m m
- 13. 13
- 14. 14
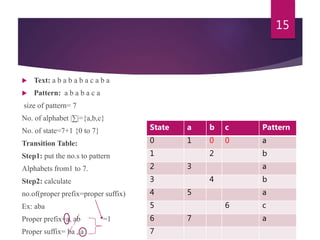
- 15. ïĩ Text: a b a b a b a c a b a ïĩ Pattern: a b a b a c a size of pattern= 7 No. of alphabet |â|={a,b,c} No. of state=7+1 {0 to 7} Transition Table: Step1: put the no.s to pattern Alphabets from1 to 7. Step2: calculate no.of(proper prefix=proper suffix) Ex: aba Proper prefix=a, ab =1 Proper suffix= ba , a 15 State a b c Pattern 0 1 0 0 a 1 2 b 2 3 a 3 4 b 4 5 a 5 6 c 6 7 a 7
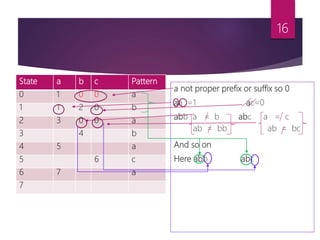
- 16. a not proper prefix or suffix so 0 aa =1 ac=0 abb a = b abc a = c ab = bb ab = bc And so on Here abb abc 16 State a b c Pattern 0 1 0 0 a 1 1 2 0 b 2 3 0 0 a 3 4 b 4 5 a 5 6 c 6 7 a 7
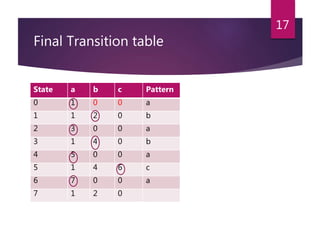
- 17. Final Transition table 17 State a b c Pattern 0 1 0 0 a 1 1 2 0 b 2 3 0 0 a 3 1 4 0 b 4 5 0 0 a 5 1 4 6 c 6 7 0 0 a 7 1 2 0
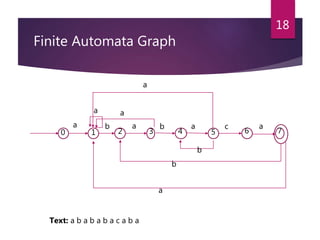
- 18. Finite Automata Graph 18 60 1 2 53 4 7 a b a b a c a a a a b a b Text: a b a b a b a c a b a
- 19. Real life uses of DFA 1. GREP 2. COKE MACHINE 3. THERMOSTATS (FRIDGE) 4. ELEVATORS 5. TRAIN TRACK SWITCHES 19
- 20. Reference 1. REIF, JOHN. HTTPS://WWW.YOUTUBE.COM/WATCH?V=UH MFMBPKIH4 2.CORMEN, ET AL. INTRODUCTION TO ALGORITHMS. ÂĐ1990 MIT PRESS, CAMBRIDGE. 862-868. 20
- 21. 21 Thank You