Fluid mechanics
- 3. Its specific gravity (relative density) is equal to the ratio of its density to that of water at standard temperature and pressure. W = Îģ ÎģL W L L Ï Ï =S Its specific gravity (relative density) is equal to the ratio of its density to that of either air or hydrogen at some specified temperature and pressure. ah G Îģ Îģ = ah G G Ï Ï =S where: At standard condition W = 1000 kg/m3 W = 9.81 KN/m3
- 4. Atmospheric pressure: The pressure exerted by the atmosphere. At sea level condition: Pa = 101.325 KPa = .101325 Mpa = 1.01325Bar = 760 mm Hg = 10.33 m H2O = 1.133 kg/cm2 = 14.7 psi = 29.921 in Hg = 33.878 ft H2O Absolute and Gage Pressure Absolute Pressure: is the pressure measured referred to absolute zero and using absolute zero as the base. Gage Pressure: is the pressure measured referred to atmospheric pressure, and using atmospheric pressure as the base
- 5. Atmospheric Pressure ï§ Atmospheric pressure is normally about 100,000 Pa ï§ Differences in atmospheric pressure cause winds to blow ï§ Low atmospheric pressure inside a hurricaneâs eye contributes to the severe winds and the development of the storm surge
- 6. x dx v+dv v moving plate Fixed plate v S dv/dx S = (dv/dx) S = (v/x) = S/(v/x) where: - absolute or dynamic viscosity in Pa-sec S - shearing stress in Pascal v - velocity in m/sec x -distance in meters
- 7. r h Where: - surface tension, N/m - specific weight of liquid, N/m3 r â radius, m h â capillary rise, m C 0 0.0756 10 0.0742 20 0.0728 30 0.0712 40 0.0696 60 0.0662 80 0.0626 100 0.0589 Surface Tension of Water r cos2 h Îģ ÎļÏ
- 8. MANOMETERS Manometer is an instrument used in measuring gage pressure in length of some liquid column. ï§ Open Type Manometer : It has an atmospheric surface and is capable in measuring gage pressure. ï§ Differential Type Manometer : It has no atmospheric surface and is capable in measuring differences of pressure. Pressure Head: where: p - pressure in KPa - specific weight of a fluid, KN/m3 h - pressure head in meters of fluid h P Îģ
- 9. In steady flow the velocity of the fluid particles at any point is constant as time passes. Unsteady flow exists whenever the velocity of the fluid particles at a point changes as time passes. Turbulent flow is an extreme kind of unsteady flow in which the velocity of the fluid particles at a point change erratically in both magnitude and direction. Types of flowing fluids:
- 10. More types of fluid flow ï§ Fluid flow can be compressible or incompressible. ï§ Most liquids are nearly incompressible. ï§ Fluid flow can be viscous or nonviscous.
- 11. When the flow is steady, streamlines are often used to represent the trajectories of the fluid particles.
- 12. 222 2 vA t m 111 1 vA t m Vm The Equation of Continuity ïŧ distance tvA
- 13. 222111 vAvA EQUATION OF CONTINUITY The mass flow rate has the same value at every position along a tube that has a single entry and a single exit for fluid flow. SI Unit of Mass Flow Rate: kg/s
- 14. Open Type Manometer Open Manometer Fluid Fluid A Differential Type Manometer Fluid B Manometer Fluid Fluid A
- 15. Determination of S using a U - Tube x y Open Open Fluid A Fluid B SAx = SBy
- 16. Energy and Head Bernoullis Energy equation: Reference Datum (Datum Line) 1 2 z1 Z2 HL = U - Q
- 17. ï§ BERNOULLIâS EQUATION ï§ In steady flow of a nonviscous, incompressible fluid, the pressure, the ï§ fluid speed, and the elevation at two points are related by:
- 18. 1. Without Energy head added or given up by the fluid (No work done by the system or on the system: L2 2 22 t1 2 11 H+Z+ 2g v + Îģ P =h+Z+ 2g v + Îģ P L2 2 22 1 2 11 H+Z+ 2g v + Îģ P =Z+ 2g v + Îģ P h+H+Z+ 2g v + Îģ P =+Z+ 2g v + Îģ P L2 2 22 1 2 11 2. With Energy head added to the Fluid: (Work done on the system 3. With Energy head added given up by the Fluid: (Work done by the Where: P â pressure, KPa - specific weight, KN/m3 v â velocity in m/sec g â gravitational acceleration Z â elevation, meters m/sec2 + if above datum H â head loss, meters - if below datum
- 19. Ventury Meter A. Without considering Head loss flowltheoreticaQ vAvAQ Z g2 vP Z g2 vP 2211 2 2 22 1 2 11 ÎģÎģ Manometer 1 2 B. Considering Head loss flowactual'Q vAvA'Q HZ g2 vP Z g2 vP 2211 L2 2 22 1 2 11 ÎģÎģ Meter Coefficient Q 'Q C
- 20. Orifice: An orifice is an any opening with a closed perimeter Without considering Head Loss 1 2 a a Vena Contractah By applying Bernoulli's Energy theorem: 2 2 22 1 2 11 Z g2 vP Z g2 vP But P1 = P2 = Pa and v1is negligible, then 21 2 2 ZZ g2 v and from figure: Z1 - Z2 = h, therefore h g2 v 2 2 gh2v2 Let v2 = vt gh2vt where: vt - theoretical velocity, m/sec h - head producing the flow, meters g - gravitational acceleration, m/sec2
- 21. velocityltheoretica velocityactual v C t v v' Cv orificetheofarea contractavena@jetofarea Cc A a Cc dischargeltheoretica dischargeactual v C Q Q' Cd vcd CCC where: v' - actual velocity vt - theoretical velocity a - area of jet at vena contracta A - area of orifice Q' - actual flow Q - theoretical flow Cv - coefficient of velocity Cc - coefficient of contraction Cd - coefficient of discharge
- 22. Lower Reservoir Upper Reservoir Suction Gauge Discharge Gauge Gate Valve Gate Valve
- 23. metersHZZ 2g vvPP H L12 2 1 2 212 t Îģ Q = Asvs = Advd m3/sec WP = Q Ht KW KW 60,000 TN2 BP Ï
- 24. HYDRO ELECTRIC POWER PLANT Headrace Tailrace Y â Gross Head Penstock turbine 1 2
- 25. Headrace Tailrace Y â Gross Head Penstock ZB 1 2 Draft Tube B Generator B â turbine inlet
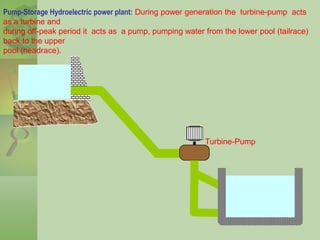
- 26. Pump-Storage Hydroelectric power plant: During power generation the turbine-pump acts as a turbine and during off-peak period it acts as a pump, pumping water from the lower pool (tailrace) back to the upper pool (headrace). Turbine-Pump
- 27. ï§THANK YOU !!!