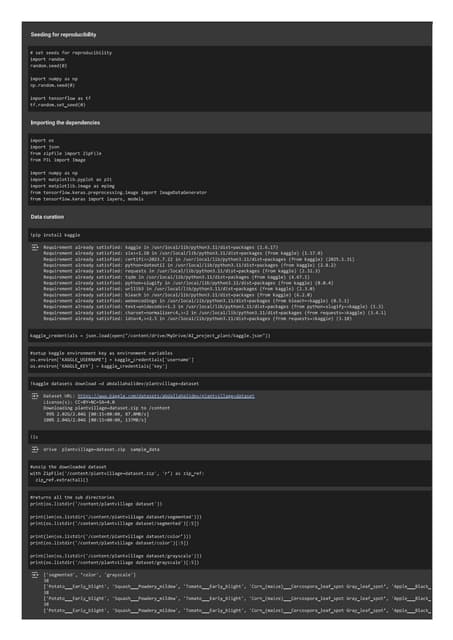
FORECASTING 2015-17.pptx
- 2. 2 Road Map ïŊ Role of Forecasting ïŊ Forecasting Approaches ïŊ Qualitative forecasting ïŊ Quantitative forecasting ïŊ Time Series Models ïŊ Regression Methods ïŊ Forecast Accuracy Focus Forecasting
- 3. 3 Forecasting ïŊ Predicting the Future ïŊ Vital for business organization ïū Underlying basis of all business decisions ïū Most techniques assume an underlying stability in the system ïū Qualitative Forecasting Approach: ïū Quantitative Forecasting Approach:
- 4. 4
- 5. 5
- 6. 6
- 7. 7
- 8. 8
- 9. 9
- 10. 10
- 11. 11
- 12. 12
- 13. 13
- 14. 14
- 15. 15
- 16. 16
- 17. 17 Qualitative Methods ïŊ Grass root method â going down to the lowest level of hierarchy ïŊ Market research â data collection and hypothesis testing ïŊ Jury of âexecutive opinionâ â source of internal qualitative forecast ïŊ Historical analogy â history or past data of the item ïŊ Panel consensus â free open exchange in between select few ïŊ Delphi Method - Iterative group process ïū 3 types of participants ïū Decision makers: Evaluate responses and make decisions ïū Staff: Administering survey ïū Respondents: People who can make valuable judgments
- 18. 18 Quantitative Forecasting Time Series Models: ïū Set of evenly spaced numerical data - Obtained by observing response variable at regular time periods ïū Forecast based only on past values - Assumes that factors influencing past and present will continue influence in future 1. Naive approach 2. Moving averages 3. Exponential smoothing 4. Trend projection Associative Models / Causal Models: 1. Linear regression
- 19. 19 Demand Behavior ïŊ Trend ïŪ Persistent, overall upward or downward pattern ïŪ Changes due to population, technology, age, culture, etc. ïŊ Cycle ïŪ an up-&-down repetitive movement in demand over a length of span ïŪ due to business cycle; political and economic factors ïŊ Seasonal pattern ïŪ is often weather / festival / event / specific period related ïŪ oscillating in nature - usually occurs within a single year ïŊ Random variations ïŪ Erratic; unsystematic; short duration non-repeating ïŪ unpredictable and have no âassignable causesâ
- 20. 20 Time (a) Trend Time (d) Trend with seasonal pattern Time (c) Seasonal pattern Time (b) Cycle Demand Demand Demand Demand Random movement Forms of Forecast Movement
- 21. Demand for product or service | | | | 1 2 3 4 Year Average demand over four years Seasonal peaks Trend component Actual demand Random variation Components of Demand
- 22. 22 Moving Average ïŊ Naive Forecast / Intuitive Forecast ïŪ Demand of the current period is used as next periodâs forecast ïŪ Does not take into account historical behavior ïŪ Reacts directly to the normal, random movements of the demand ïŪ Cost effective and sometimes very efficient ïŊ Simple Moving Average ïŪ Uses several demand values during the recent past to forecast ïŪ Tends to âsmoothenâ or âdampenâ, the random variations in single period forecast ïŪ Preferable for stable demand with no pronounced behavioral patterns ïŪ Computed for specific number of periods depending on how the forecaster desires to âsmoothenâ the demand data ïŪ The longer the moving average period, the smoother it will be. ïŪ Alternatively, a shorter is more susceptible to simple random variations
- 23. 23 NaÃŊve Approach Jan 120 Feb 90 Mar 100 Apr 75 May 110 June 50 July 75 Aug 130 Sept 110 Oct 90 ORDERS MONTH PER MONTH - 120 90 100 75 110 50 75 130 110 90 Nov - FORECAST
- 24. 24 Simple Moving Average MAn = n i = 1 ï Di n where n = number of periods in the moving average Di = demand in period i
- 25. 25 3 Month Simple Moving Average Jan 120 Feb 90 Mar 100 Apr 75 May 110 June 50 July 75 Aug 130 Sept 110 Oct 90 Nov - ORDERS MONTH PER MONTH MA3 = 3 i = 1 ï Di 3 = 120 + 90 + 100 3 = 103.3 orders for Apr. â â â 103.3 88.3 95.0 78.3 78.3 85.0 105.0 110.0 MOVING AVERAGE
- 26. 26 5 Month Simple Moving Average Jan 120 Feb 90 Mar 100 Apr 75 May 110 June 50 July 75 Aug 130 Sept 110 Oct 90 Nov - ORDERS MONTH PER MONTH MA5 = 5 i = 1 ï Di 5 = 90 + 110 + 130+75+50 5 = 91 orders for Nov. â â â â â 99.0 85.0 82.0 88.0 95.0 91.0 MOVING AVERAGE
- 27. 27 Smoothing Effects 150 â 125 â 100 â 75 â 50 â 25 â 0 â | | | | | | | | | | | Jan Feb Mar Apr May June July Aug Sept Oct Nov Actual Orders Month 5-month 3-month
- 28. 28 Weighted Moving Average ïŊ Adjusts moving average method to more closely reflect data fluctuations ï§Weights are assigned to most recent data, barring in case of seasonal cycles ï§Precise weights are decided thorough trial and error (based on experience and intuition), as does the number of periods to be considered ï§If recent periods are weighted too heavily, the forecast might over-react to a random fluctuation in demand ï§If they are weighted too lightly, the forecast might under-react to actual changes in demand pattern
- 29. 29 Weighted Moving Average WMAn = i = 1 ï Wi Di where Wi = the weight for period i, between 0 and 100 percent ï Wi = 1.00
- 30. 30 Weighted Moving Average MONTH WEIGHT DATA August 17% 130 September 33% 110 October 50% 90 WMA3 = 3 i = 1 ï Wi Di = (0.50) (90) + (0.33) (110) + (0.17) (130) = 103.4 orders November Forecast
- 31. 31 ï§ Averaging method - weights most recent data more strongly ï§ As the past becomes more distant, the imp. of data diminishes ï§ So very useful and preferable method, if recent changes are significant and unpredictable ï§ Widely used, most popular because its an accurate method ï§ Requires minimal data: ï§forecast for the current period, ï§actual demand for the current period and ï§a weighing factor OR smoothing constant. Exponential Smoothing
- 32. 32 Ft+1 = ï ïĄ *ï Dt + (1 - ïĄ) * Ft where: Ft + 1 =forecast for next period Dt = actual demand for present period Ft = previously determined forecast for present period ïĄï = weighting factor, smoothing constant â determines the level of smoothing *Assume first forecast as Actual DemandâĶ Exponential Smoothing
- 33. 33 Effect of Smoothing Constant 0.0 ïĢï ïĄï ïĢ 1.0 reflects the weight given to the most recent demand data If ïĄï = 0.20, then Ft + 1 = 0.20 * Dt + 0.8 * Ft If ïĄï = 0, then Ft + 1 = Ft Forecast does not even consider recent actual data If ïĄï = 1, then Ft + 1 = 1 * Dt + 0 * Ft = Dt Forecast based only on most recent data, so this becomes as good as naÃŊve forecast
- 34. 34 F2 = ïĄ D1 + (1- ïĄ) F1 = (0.30) 37 + (1- 0.3) 37 = 37 F3 = ïĄ D2 + (1- ïĄ) F2 = (0.30) 40 + (1- 0.3) 37 = 37.90 F13 = ïĄ D12 + (1- ïĄ) F12 = (0.30) 54 + (1- 0.3) 50.84 = 51.79 Exponential Smoothing (Îą = 0.30) PERIOD MONTH DEMAND 1 Jan 37 2 Feb 40 3 Mar 41 4 Apr 37 5 May 45 6 Jun 50 7 Jul 43 8 Aug 47 9 Sep 56 10 Oct 52 11 Nov 55 12 Dec 54
- 35. 35 FORECAST, Ft + 1 PERIOD MONTH DEMAND (ïĄ = 0.3) (ïĄ = 0.5) 1 Jan 37 â â 2 Feb 40 37.00 37.00 3 Mar 41 37.90 38.50 4 Apr 37 38.83 39.75 5 May 45 38.28 38.37 6 Jun 50 40.29 41.68 7 Jul 43 43.20 45.84 8 Aug 47 43.14 44.42 9 Sep 56 44.30 45.71 10 Oct 52 47.81 50.85 11 Nov 55 49.06 51.42 12 Dec 54 50.84 53.21 13 Jan â 51.79 53.61 Exponential Smoothing
- 36. 36 70 â 60 â 50 â 40 â 30 â 20 â 10 â 0 â | | | | | | | | | | | | | 1 2 3 4 5 6 7 8 9 10 11 12 13 Actual Orders Month Exponential Smoothing ïĄ = 0.50 ïĄ = 0.30
- 37. 37 Regression Methods ïŊ Linear Regression ïŪ Regression can be defined as functional relationship between two or more correlated variables ïŪ Regression is used for forecasting by establishing a mathematical relationship between two or more variables (demand and some other independent variable) in the form of a linear equation ïŪ It is used to predict one variable given the other ïŪ Linear regression refers to the special class of regression where the relationship between the variable forms a straight line ïŪ Good for long range forecasting and aggregate planning
- 38. 38 Linear Regression is a causal method of forecasting in which a mathematical relationship is developed between demand and time. Linear trend line relates a dependent variable (demand) to an independent variable (time) in the form of a linear equation: y = a + bx a = intercept b = slope of the line x = time period y = demand forecast for period x Linear Trend Line b = a = y - b x where n = number of periods x = = mean of the x values y = = mean of the y values ïï xy - nxy ïï x2 - nx2 ïï x n ïï y n
- 39. 39 Least Squares Example x (PERIOD) y (DEMAND) x y x2 1 37 37 1 2 40 80 4 3 41 123 9 4 37 148 16 5 45 225 25 6 50 300 36 7 43 301 49 8 47 376 64 9 56 504 81 10 52 520 100 11 55 605 121 12 54 648 144 78 557 3867 650
- 40. 40 x = = 6.5 y = = 46.42 b = = =1.72 a = y - bx = 46.42 - (1.72)(6.5) = 35.2 3867 - (12)(6.5)(46.42) 650 - 12(6.5)2 ïĨxy - nxy ïĨx2 - nx2 78 12 557 12 Least Squares Example
- 41. 41 Linear Trend Line y = 35.2 + 1.72x Forecast for Period 13 y = 35.2 + 1.72(13) = 57.56 units 70 â 60 â 50 â 40 â 30 â 20 â 10 â 0 â | | | | | | | | | | | | | 1 2 3 4 5 6 7 8 9 10 11 12 13 Actual Demand Period Linear trend line
- 42. 42 Linear Regression Example x y adv spend sales xy x2 4 36.3 145.2 16 6 40.1 240.6 36 6 41.2 247.2 36 8 53.0 424.0 64 6 44.0 264.0 36 7 45.6 319.2 49 5 39.0 195.0 25 7 47.5 332.5 49 49 346.7 2167.7 311
- 43. 43 Linear Regression Example (cont.) x = = 6.125 y = = 43.36 b = = = 4.06 a = y - bx = 43.36 - (4.06)(6.125) = 18.46 49 8 346.9 8 ïĨxy - nxy ïĨx2 - nx2 (2,167.7) - (8)(6.125)(43.36) (311) - (8)(6.125)2
- 44. 44 | | | | | | | | | | | 0 1 2 3 4 5 6 7 8 9 10 60,000 â 50,000 â 40,000 â 30,000 â 20,000 â 10,000 â Linear regression line, y = 18.46 + 4.06x Wins, x Attendance, y Linear Regression Example (cont.) y = 18.46 + 4.06x y = 18.46 + 4.06(7) = 46.88, or 46,880 Regression equation Sales forecast for 7 lakhs of ad spend
- 45. 45 Correlation & Coefficient of Determination ï§ Correlation, r ï§ Correlation is a measure of the strength of the relationship between independent and dependent variables ï§ degree of association between two variables (-1.00 to +1.00) ï§ nil/poor/average/strong, & positive/negative ï§ Coefficient of Determination, r2 ï§ Percentage of variation in dependent variable resulting from changes in the independent variable (0% to 100%) ï§ A measure of the amount of variation in the dependent variable about its mean that is explained by the regression equation
- 46. 46 Computing Correlation nïĨ xy - ïĨ xïĨ y [nïĨ x2 - (ïĨ x)2] [nïĨ y2 - (ïĨ y)2] r = Coefficient of Determination r2 = (0.947)2 = 0.897 r = (8)(2,167.7) - (49)(346.9) [(8)(311) - (49)2] [(8)(15,224.7) - (346.9)2] r = 0.947
- 47. 47 Forecast Accuracy ïŊ A forecast is never ever accurate ïŊ Large degree of error mean ïŪ Either the forecasting technique used is applied wrongly or is not applicable in the case ïŪ Wrong relationship among variables ïŪ Or the âparametersâ used need to be adjusted for âtrendâ ïŊ Forecast Error ïŪ Difference between forecast and actual demand - Error ïŪ MAD - Mean Absolute Deviation ïŪ MAPD - Mean Absolute Percent Deviation or MAPE ïŪ Cumulative Error - RSFE ïŪ Average Error or Bias
- 48. 48 Mean Absolute Deviation (MAD) MAD: The absolute average difference between the AD & FD. where, t = period number Dt = demand in period t Ft = forecast for period t n = total number of periods ï ïšï ïš = absolute value The smaller the value of MAD relative to the magnitude of ï ïž Dt - Ft ïž n M A D =
- 49. 49 Other Accuracy Measures ïŊ MAPD: Measures the absolute error (AV-FV) as a % of demand rather than per period (MAD). Can be used across the board to measure the relative accuracy of the forecast. ïŊ Cumulative Error (RSFE): Simply computed by summing up the forecast errors. Thatâs why Linear Trend Line has zero cumulative value. ïŊ Average Error (Bias): Computed by averaging the cumulative error value (RSFE) over the number of time periods. +ve value: low, -ve value: high and zero value: no bias
- 50. 50 Other Accuracy Measures Mean Absolute Percent Deviation (MAPD) MAPD = ïĨ |Dt - Ft| ïĨDt Cumulative Error (RSFE) RSFE = ïĨ et = ïĨ (Dt â Ft) Average Error (Bias) E = ïĨ et n
- 51. 51 MAD Example 1 37 37.00 â â 2 40 37.00 3.00 3.00 3 41 37.90 3.10 3.10 4 37 38.83 -1.83 1.83 5 45 38.28 6.72 6.72 6 50 40.29 9.69 9.69 7 43 43.20 -0.20 0.20 8 47 43.14 3.86 3.86 9 56 44.30 11.70 11.70 10 52 47.81 4.19 4.19 11 55 49.06 5.94 5.94 12 54 50.84 3.15 3.15 557 49.31 53.39 PERIOD DEMAND, Dt Ft (ïĄ =0.3) (Dt - Ft) |Dt - Ft| ï ïž Dt - Ft ïž n MAD = = = 4.85 53.39 11
- 52. 52 Forecast Control ïŊ Forecast can go out of control due to various reasons ïŪ Change in trend ïŪ Unanticipated appearance of a cycle ïŪ Irregular variation such as unseasonable weather ïŪ Promotional campaign, new competition, political reasons, othersâĶ ïŊ Tracking Signal: this indicates whether the forecast average is keeping pace with any genuine upward or downward changes in demand ïŪ Monitors the forecast to see if it is biased high or low Tracking Signal = = ïĨ(Dt - Ft) MAD RSFE MAD
- 53. 53 Tracking Signal Values 37 - â â - - 40 37.00 3.00 3.00 3.00 3.00 41 37.90 3.10 6.10 6.10 3.05 37 38.83 -1.83 4.27 7.93 2.64 45 38.28 6.72 10.99 14.65 3.66 50 40.29 9.69 20.68 24.34 4.87 43 43.20 -0.20 20.48 24.54 4.09 47 43.14 3.86 24.34 28.40 4.06 56 44.30 11.70 36.04 40.10 5.01 52 47.81 4.19 40.23 44.29 4.92 55 49.06 5.94 46.17 50.23 5.02 54 50.84 3.15 49.32 53.38 4.85 DEMAND FORECAST, ERROR ïĨRSEF = +ve CE Dt Ft Dt - Ft ïĨ(Dt - Ft) ïĨïž Dt - Ft ïž MAD TS3 = = 2.00 6.10 3.05 Tracking signal for period 3 1.00 2.00 1.62 3.00 4.25 5.01 6.00 7.19 8.18 9.20 10.17 TRACKING SIGNAL
- 54. 54 Tracking Signal Plot 3ïģ â 2ïģ â 1ïģ â 0ïģ â -1ïģ â -2ïģ â -3ïģ â | | | | | | | | | | | | | 0 1 2 3 4 5 6 7 8 9 10 11 12 Tracking signal (MAD) Period Exponential smoothing (ïĄ = 0.30) Linear trend line
- 56. 56 Example
- 57. 57 Example
- 58. 58 Seasonal Adjustments ï§ Repetitive increase / decrease in demand ï§ Seasonal patterns can also occur on a periodic basis ï§ Use seasonal factor to adjust forecast ï§ A seasonal factor is a numeric value that is multiplied by the normal forecast to get a seasonally adjusted forecast ï§ A seasonal factor range from 0 to 1, it is in effect, the portion of annual demand assigned to each season ï§ Thus SF when multiplied to annual forecasted demand yield seasonally adjusted forecasts for each season Seasonal Factor = Si = Di ïĨD
- 59. 59 Seasonal Adjustment (cont.) 2002 12.6 8.6 6.3 17.5 45.0 2003 14.1 10.3 7.5 18.2 50.1 2004 15.3 10.6 8.1 19.6 53.6 Total 42.0 29.5 21.9 55.3 148.7 DEMAND (1000âS PER QUARTER) YEAR I II III IV Total SI = = = 0.28 D1 ïĨD 42.0 148.7 SII = = = 0.20 D2 ïĨD 29.5 148.7 SIV = = = 0.37 D4 ïĨD 55.3 148.7 SIII = = = 0.15 D3 ïĨD 21.9 148.7
- 60. Seasonal Adjustment (cont.) ïŊ X Y X*X X*Y ïŊ 1 45.0 1 45.00 ïŊ 2 50.1 4 100.20 ïŊ 3 53.6 9 160.80 ïŊ FIND MEAN OF X AND Y ïŊ VALUE OF a AND b 60
- 61. 61 Seasonal Adjustment (cont.) SFI = (SI) (F4) = (0.28)(58.17) = 16.28 SFII = (SII) (F4) = (0.20)(58.17) = 11.63 SFIII = (SIII) (F4) = (0.15)(58.17) = 8.73 SFIV = (SIV) (F4) = (0.37)(58.17) = 21.53 y = 40.97 + 4.30 x = 40.97 + 4.30(4) = 58.17 For 2005
- 62. 62 Forecasting Process 6. Check forecast accuracy with one or more measures 4. Select a forecast model that seems appropriate for data 5. Develop/compute forecast for period of historical data 8a. Forecast over planning horizon 9. Adjust forecast based on additional qualitative infoâ & insight 10. Monitor results and measure forecast accuracy 8b. Select new forecast model or adjust parameters of existing model 7. Is accuracy of forecast acceptable? 1. Identify the purpose of forecast 3. Plot data and identify patterns 2. Collect historical data No Yes














































![46
Computing Correlation
nïĨ xy - ïĨ xïĨ y
[nïĨ x2 - (ïĨ x)2] [nïĨ y2 - (ïĨ y)2]
r =
Coefficient of Determination
r2 = (0.947)2 = 0.897
r =
(8)(2,167.7) - (49)(346.9)
[(8)(311) - (49)2] [(8)(15,224.7) - (346.9)2]
r = 0.947](https://image.slidesharecdn.com/forecasting2015-17-231017092032-ae34edff/85/FORECASTING-2015-17-pptx-46-320.jpg)