Forecasting
- 1. Forecasting DISC 333: SUPPLY CHAIN MANAGEMENT
- 2. Forecasting in Operations Function Forecasting allows predicting future values of a series based on past observations; In supply chain the primarily interest is in forecasting product demand; Trends, cycles and seasonal variation may be present in past observations that help us to predict future demand more closely.
- 3. Forecasting Horizon in Supply Chain Planning Long (Months / Years) Capacity needs, Long-term sales patterns, Growth trends Intermediate (Weeks / Months) Product family sales, Labor needs, Resource requirements Short (Days / Weeks) Short-term sales, Shift schedule, Resource requirements
- 4. Characteristics of Forecasts They are usually wrong. A good forecast is more than a single number. Aggregate forecasts are more accurate. The longer the forecast horizon, the less accurate the forecast will be. Forecasts should not be used to the exclusion of known information.
- 5. Benefits of Forecasting Lower inventories Reduced Stock-outs Smoother production and supply-chain plans Reduced production costs Improved customer service Etc.
- 6. Forecasting Methods Qualitative (or Subjective) Methods: Forecasts based on subjective judgment or opinion Sales Force Composites Customer Surveys Jury of Executive Opinion Delphi Method Quantitative (or Objective) Methods: Forecasts are derived based on an analysis of data. Time Series Forecasting Models Causal or Associative Models
- 7. Time Series Forecasting Models Information can be inferred from the pattern of past observations and can be used to forecast future values of the series. Observations about past values are drawn at discrete points in time, usually equally spaced. Time series include various patterns of data: Trend Seasonality Cycles Randomness
- 8. Simple Moving Average Forecasting Model A moving average of order N is simply the arithmetic average of the most recent N observations. For one step ahead forecasts for most recent N observations: t â1 Ft = (1 / N ) â Ai = (1 / N )( At â1 + At â 2 + ... + At â N ) i =t â N or t ïĢŪ t â1 ïĢđ Ft +1 = (1 / N ) â Ai = (1 / N ) ïĢŊ At + â Ai â At â N ïĢš i = t â N +1 ïĢ° i =t â N ïĢŧ Ft +1 = Ft + (1 / N )[ At â At â N ]
- 9. Example: Simple Moving Average Consider a demand Period Demand MA(3) MA(6) process 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 1 2 22, 24 in which 2 4 there is a definite 3 6 4 8 4 trend. 5 10 6 6 12 8 Consider the MA(3) 7 14 10 7 8 16 12 9 and MA(6) 9 18 14 11 10 20 16 13 11 22 18 15 12 24 20 17
- 10. Simple Moving Average Forecasting Model (Excel) Period Demand Forecast MA(3) Forecast MA(6) Moving Average MA(3) 1 2 #N/A #N/A 30 25 2 3 #N/A #N/A 20 Value 15 3 10 5 #N/A 10 Actual 5 Forecast 4 8 7 #N/A 0 1 2 3 4 5 6 7 8 9 10 11 12 5 12 10 #N/A Data Point 6 18 12.66666667 8.833333333 7 24 18 12.5 Moving Average MA(6) 8 26 22.66666667 16.33333333 30 9 20 23.33333333 18 Value 20 10 16 20.66666667 19.33333333 10 Actual 0 Forecast 11 22 19.33333333 21 1 2 3 4 5 6 7 8 9 10 11 12 12 24 20.66666667 22 Data Point Con: Less responsive to changes in demand.
- 11. Weighted Moving Average Forecasting Model t Ft +1 = âw A i =t â N +1 i i Allows more emphasis to be placed on recent or past data. Weights can be determined by experience of the forecaster. Still not responsive enough to track changes in demand.
- 12. Weighted Moving Average (Example) Perio d Demand Weights Forecast MA(3) 30 1 2 0.2 25 2 3 0.2 20 3 10 0.6 15 Actual 4 8 7 Forecast 10 5 12 7.4 6 18 10.8 5 7 24 14.8 0 1 2 3 4 5 6 7 8 9 10 11 12 8 26 20.4 9 20 24 10 16 22 11 22 18.8 12 24 20.4
- 13. Exponential Smoothing Forecasting Model Is a sophisticated weighted moving average technique. Forecast for next periodâs demand is the current periodâs forecast adjusted by a fraction of the difference between the current periodâs actual demand and its forecast. Requires less data to be implemented, thus is more widely practiced technique. Suitable for data that show little trend or seasonal patterns. Ft = Îą At â1 + (1 â Îą ) Ft â1 where 0 < Îą âĪ 1 is the smoothing constant, determines relative weight placed on demand Ft = Ft â1 â Îą ( Ft â1 â At â1 ) Ft = Ft â1 â Îą et â1
- 14. Exponential Smoothing Forecasting Model If we forecast high in period t-1, et-1 is positive and the adjustment is to decrease the forecast. And vice versa. If Îą is large, more weight is given to the current observation and less weight on past observations, which results into a forecast that will react quickly to changes in the demand pattern but may have much greater variation from period to period.
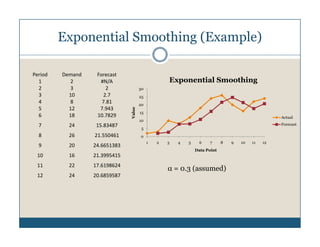
- 15. Exponential Smoothing (Example) Period Demand Forecast 1 2 #N/A Exponential Smoothing 2 3 2 30 3 10 2.7 25 4 8 7.81 20 5 12 7.943 Value 15 6 18 10.7829 Actual 10 7 24 15.83487 Forecast 5 8 26 21.550461 0 1 2 3 4 5 6 7 8 9 10 11 12 9 20 24.6651383 Data Point 10 16 21.3995415 11 22 17.6198624 Îą = 0.3 (assumed) 12 24 20.6859587
- 16. Trend Based Exponential Smoothing Forecasting Model Ft = Îą At â1 + (1 â Îą )( Ft â1 + Tt â1 ) Tt = Îē ( Ft â Ft â1 ) + (1 â Îē )Tt â1 and the trend - adjusted forecast is TAFt + m = Ft + mTt Higher the Îē higher the emphasis on recent trend changes. Îą & Îē are determined by trial and error approach.
- 17. Linear Trend Forecasting Model Simple linear regression can be used to fit a line to the time series historical data. Linear trend method minimizes the sum of squared deviations to determine the characteristics of the linear equation: ( x1 , y1 ), ( x2 , y2 ),..., ( xn , yn ) be n paired data points for X & Y X = Independent Variable Y = Dependent Variable Suppose a linear relationship exists between X and Y, then ⧠Y = b +b X 0 1
- 18. Linear Trend Forecasting Model ⧠where, Y = predicted value of Y x = time variable b 0 = intercept of the line, and b1 = slope of the line nâ ( xy ) â â x â y b1 = nâ x 2 â (â x ) 2 b0 = â y âb â x1 n
- 19. Linear Trend Forecasting Model (Example) What is the trend line and forecast for Period-13 for the following data? Period Demand Period Demand Period Demand 1 1600 5 2500 9 3900 2 2200 6 3500 10 4700 3 2000 7 3300 11 4300 4 1600 8 3200 12 4400
- 20. Linear Trend Forecasting Model (Example) Period Demand b1 = [12(282,800) â 78(37,200)] / (x) (y) x2 xy [12(650) -78*78] 1 1600 1 1600 = 286.71 2 2200 4 4400 3 2000 9 6000 4 1600 16 6400 âĒ b0 = [37,000 â 286.71(78)]/12 5 2500 25 12500 = 1,236.4 6 3500 36 21000 7 3300 49 23100 8 3200 64 25600 Y = 1,236.4 + 286.71 x 9 3900 81 35100 10 4700 100 47000 11 4300 121 47300 F13 = 1236.4 + 286.71 (13) = 4963.5 12 4400 144 52800 ây = âx2 = âxy = 37200 650 282,800
- 21. Linear Trend Forecasting Model (Example) Period (x) Demand (y) Forecast 1 1600 1523.0769 5000 2 2200 1809.7902 4500 3 2000 2096.5035 4000 4 1600 2383.2168 3500 5 2500 2669.9301 3000 6 3500 2956.6434 2500 Actual 7 3300 3243.3566 2000 Forecast 8 3200 3530.0699 1500 9 3900 3816.7832 1000 10 4700 4103.4965 500 0 11 4300 4390.2098 1 2 3 4 5 6 7 8 9 10 11 12 12 4400 4676.9231 Slope 286.7132867 Intercept 1236.363636
- 22. Associative Models One or several external variables are identified that are related to demand, which are easier to determine than demand. Once the relationship between the external variable and demand is determined, it can be used as a forecasting tool. Y = Phenomenon to be forecasted X1 , X2 ,âĶ, Xn = Variables affecting the phenomenon, then Y = f(X1 , X2 ,âĶ, X n)
- 23. Forecast Accuracy At = observed demand during periods t, assume {At , t âĨ 1} Ft = forecast made for period t during period t-1, one step ahead forecast et = forecast error, then et = Ft â At If e1 , e2 ,..., en = forecast errors observed over n periods n MAD = mean absolute deviation = (1 / n)â ei i =1 n MSE = mean squared error = (1 / n)â ei2 i =1 n MAPE = mean absolute percentage error = (1 / n)â ei / Di i =1
- 24. Forecast Accuracy n Running sum of forecast errors (RSFE) = âe t =1 t RSFE TrackingSignal = MAD A number of parameters have been defined. Each one of which provide some sort of advantage over the other. Many organizations set targets for Tracking Signal as a means to improve their forecasts.
- 25. Collaborative Planning, Forecasting, and Replenishment (CPFR) The objective of CPFR is to optimize the supply chain by improving demand forecasting, delivering the right product at the right time to the right location, reducing inventories across the supply chains, avoiding stock-outs, and improving customer service. The real value of CPFR comes from an exchange of forecasting information rather than from more sophisticated forecasting algorithms to improve forecasting accuracy.
- 26. CPFR Process








![Simple Moving Average Forecasting Model
A moving average of order N is simply the arithmetic
average of the most recent N observations.
For one step ahead forecasts for most recent N
observations:
t â1
Ft = (1 / N ) â Ai = (1 / N )( At â1 + At â 2 + ... + At â N )
i =t â N
or
t
ïĢŪ t â1
ïĢđ
Ft +1 = (1 / N ) â Ai = (1 / N ) ïĢŊ At + â Ai â At â N ïĢš
i = t â N +1 ïĢ° i =t â N ïĢŧ
Ft +1 = Ft + (1 / N )[ At â At â N ]](https://image.slidesharecdn.com/forecasting-101208093309-phpapp02/85/Forecasting-8-320.jpg)










![Linear Trend Forecasting Model (Example)
Period Demand b1 = [12(282,800) â 78(37,200)] /
(x) (y) x2 xy [12(650) -78*78]
1 1600 1 1600
= 286.71
2 2200 4 4400
3 2000 9 6000
4 1600 16 6400 âĒ b0 = [37,000 â 286.71(78)]/12
5 2500 25 12500 = 1,236.4
6 3500 36 21000
7 3300 49 23100
8 3200 64 25600 Y = 1,236.4 + 286.71 x
9 3900 81 35100
10 4700 100 47000
11 4300 121 47300 F13 = 1236.4 + 286.71 (13) = 4963.5
12 4400 144 52800
ây = âx2 = âxy =
37200 650 282,800](https://image.slidesharecdn.com/forecasting-101208093309-phpapp02/85/Forecasting-20-320.jpg)





