Fractions with pattern blocks (worksheet 9 a).pptx
- 1. Fractions with Pattern Blocks
- 2. Topics Addressed ŌĆó Fractional relationships ŌĆó Measurement of area ŌĆó Theoretical probability ŌĆó Equivalent fractions ŌĆó Addition and subtraction of fractions with unlike denominators ŌĆó Multiplication and division of fractions ŌĆó Lines of symmetry ŌĆó Rotational symmetry ŌĆó Connections among mathematical ideas
- 3. Pattern Block Pieces ŌĆó Explore the relationships that exist among the shapes.
- 4. Sample Questions for Student Investigation ŌĆó The red trapezoid is what fractional part of the yellow hexagon? ŌĆó The blue rhombus is what fractional part of the yellow hexagon? ŌĆó The green triangle is what fractional part of the yellow hexagon? the blue rhombus? the red trapezoid? ŌĆó The hexagon is how many times bigger than the green triangle?
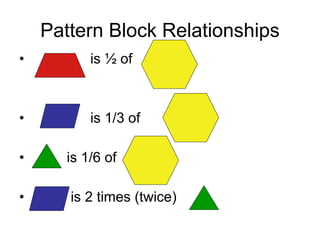
- 5. Pattern Block Relationships ŌĆó is ┬Į of ŌĆó is 1/3 of ŌĆó is 1/6 of ŌĆó is 2 times (twice)
- 6. More Pattern Block Relationships ŌĆó is ┬Į of ŌĆó is 3 times ŌĆó is 3 times ŌĆó is 1.5 times
- 7. Connections Among Mathematical Ideas ŌĆó Suppose the hexagons on the right are used for dart practice. ŌĆō If the red and white hexagon is the target, what is the probability that the dart will land on the trapezoid? Explain your reasoning. ŌĆō If the green and white hexagon is the target, what is the probability that the dart will land on a green triangle? Why?
- 8. Sample Student Problems ŌĆó Using only blue and green pattern blocks, completely cover the hexagon so that the probability of a dart landing on Ō¢¬ blue will be 2/3. Ō¢¬ green will be 2/3.
- 9. Equivalent Fractions I ŌĆó Since one green triangle is 1/6 of the yellow hexagon, what fraction of the hexagon is covered by 2 green triangles? ŌĆó Since 2 green triangles can be traded for 1 blue rhombus (1/3 of the yellow hexagon), then 2/6 = ? ŌĆó Using the stacking model and trading the hexagon for 3 blue rhombi show 1 blue rhombus on top of 3 blue rhombi.
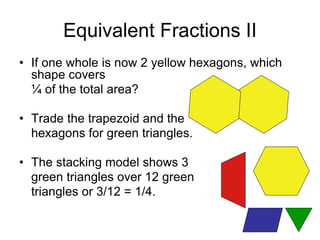
- 10. Equivalent Fractions II ŌĆó If one whole is now 2 yellow hexagons, which shape covers ┬╝ of the total area? ŌĆó Trade the trapezoid and the hexagons for green triangles. ŌĆó The stacking model shows 3 green triangles over 12 green triangles or 3/12 = 1/4.
- 11. Equivalent Fractions III ŌĆó If one whole is now 2 yellow hexagons, which shape covers 1/3 of the total area? ŌĆó One approach is to cover 1/3 of each hexagon using 1 blue rhombus. ŌĆó Trade the blue rhombi and hexagons for green triangles. ŌĆó Then the stacking model shows 1/3 = 4/12.
- 12. Adding Fractions I ŌĆó If the yellow hexagon is 1, the red trapezoid is ┬Į, the blue rhombus is 1/3, and the green triangle is 1/6, then Ō¢¬ 1 red + 1 blue is equivalent to ┬Į + 1/3 Placing the red and blue on top of the yellow covers 5/6 of the hexagon. This can be shown by exchanging (trading) the red and blue for green triangles.
- 13. Adding Fractions II ŌĆó 1/3 + 1/6 = ? Ō¢¬ Cover the yellow hexagon with 1 blue and 1 green. Ō¢¬ ┬Į of the hexagon is covered. Ō¢¬ Exchange the blue for greens to verify. ŌĆó 1 red + 1 green=1/2 + 1/6=? Ō¢¬ Cover the yellow hexagon with 1 red and 1 green. Ō¢¬ Exchange the red for greens and determine what fractional part of the hexagon is covered by greens. Ō¢¬ 4/6 of the hexagon is covered by green. Ō¢¬ Exchange the greens for blues to find the simplest form of the fraction. Ō¢¬ 2/3 of the hexagon is covered by blue.
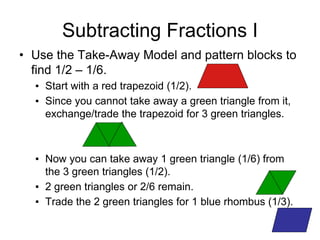
- 14. Subtracting Fractions I ŌĆó Use the Take-Away Model and pattern blocks to find 1/2 ŌĆō 1/6. Ō¢¬ Start with a red trapezoid (1/2). Ō¢¬ Since you cannot take away a green triangle from it, exchange/trade the trapezoid for 3 green triangles. Ō¢¬ Now you can take away 1 green triangle (1/6) from the 3 green triangles (1/2). Ō¢¬ 2 green triangles or 2/6 remain. Ō¢¬ Trade the 2 green triangles for 1 blue rhombus (1/3).
- 15. Subtracting Fractions II ŌĆó Use the Comparison Model to find 1/2 - 1/3. Ō¢¬ Start with a red trapezoid (1/2 of the hexagon). Ō¢¬ Place a blue rhombus (1/3 of the hexagon) on top of the trapezoid. Ō¢¬ What shape is not covered? Ō¢¬ 1/2 - 1/3 = 1/6
- 16. Multiplying Fractions I ŌĆó If the yellow hexagon is 1, then ┬Į of 1/3 can be modeled using the stacking model as ┬Į of a blue rhombus (a green triangle). Thus ┬Į * 1/3 = 1/6.
- 17. Multiplying Fractions II ŌĆó If the yellow hexagon is 1, then 1/4 of 2/3 can be modeled as 1/4 of two blue rhombi. Thus 1/4 * 2/3 = 1/6 (a green triangle).
- 18. Multiplying Fractions III ŌĆó If one whole is now 2 yellow hexagons, then 3/4 of 2/3 can be represented by first covering 2/3 of the hexagons with 4 blue rhombi and then covering ┬Š of the blue rhombi with green triangles. ŌĆó How many green triangles does it take? ŌĆó The stacking model shows that ┬Š * 2/3 = 6/12. ŌĆó Trading green triangles for the fewest number of blocks in the stacking model would show 1 yellow hexagon on top of two yellow hexagons or 6/12 = ┬Į.
- 19. Dividing Fractions 1 ŌĆó How many 1/6ŌĆÖs (green triangles) does it take to cover 1/2 (a red trapezoid) of the yellow hexagon? 1/2 ├Ę 1/6 = ?
- 20. Dividing Fractions 2 ŌĆó How many 1/6ŌĆÖs (green triangles) does it take to cover 2/3 (two blue rhombi) of the yellow hexagon? 2/3 ├Ę 1/6 = ?
- 21. Symmetry ŌĆó A yellow hexagon has 6 lines of symmetry since it can be folded into identical halves along the 6 different colors shown below (left). ŌĆó A green triangle has 3 lines of symmetry since it can be folded into identical halves along the 3 different colors shown above (right).
- 22. More Symmetry ŌĆó How many lines of symmetry are in a blue rhombus? ŌĆó Explain why a red trapezoid has only one line of symmetry.
- 23. Rotational Symmetry ŌĆó A yellow hexagon has rotational symmetry since it can be reproduced exactly by rotating it about an axis through its center. ŌĆó A hexagon has 60┬║, 120┬║, 180┬║, 240┬║, and 300┬║ rotational symmetry.
- 24. Pattern Block Cake Student Activity ŌĆó CarolineŌĆÖs grandfather Gordy owns a bakery and has agreed to make a Pattern Block Cake to sell at her schoolŌĆÖs Math Day Celebration. ŌĆó This cake will consist of ŌĆō chocolate cake cut into triangles, ŌĆō yellow cake cut into rhombi, ŌĆō strawberry cake cut into trapezoids, ŌĆō and white cake cut into hexagons. ŌĆó Like pattern blocks, the cake pieces are related to each other. ŌĆó Adapted from NCTM Addenda Series/Grades 5-8 Understanding Rational Numbers and Proportions Activity 5
- 25. Pattern Block Cake Student Activity ŌĆó If each triangular piece costs $1.00, how much will the other pieces cost? How much will the whole cake cost? ŌĆó If each whole Pattern Block Cake costs $1.00, how much will each piece cost? Adapted from NCTM Addenda Series/Grades 5-8 Understanding Rational Numbers and Proportions Activity 5
- 26. Websites for Additional Exploration ŌĆó National Library of Virtual Manipulatives http://nlvm.usu.edu/en/nav/vlibrary.html ŌĆó Online Pattern Blocks http://ejad.best.vwh.net/java/patterns/patte rns_j.shtml