Funcions
- 1. Funcions
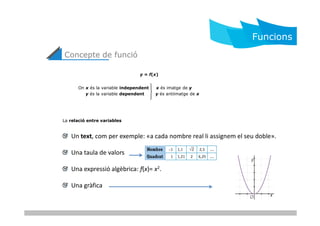
- 2. Funcions Concepte de funciÃģ y = f(x)) On x ÃĐs la variable independent x ÃĐs imatge de y y ÃĐs la variable dependent y ÃĐs antiimatge de x La relaciÃģ entre variables Un text, com per exemple: ÂŦa cada nombre real li assignem el seu dobleÂŧ. Una taula de valors Una expressiÃģ algÃĻbrica: f(x)= x2. Una grà fica
- 3. El conjunt dels valors reals de la variable independent que tenen per imatge un nombre real constitueixen el domini de la funciÃģ (D f ). El conjunt de totes les imatges reals de la funciÃģ ÃĐs el recorregut o rang de la funciÃģ (R f ). Domini i recorregut dâuna funciÃģ Funcions
- 4. Funcions algÃĻbriques Funcions polinÃēmiques Funcions f(x)=A(x), on Ax ÃĐs un polinomi. Exemples: la funciÃģ lineal, la funciÃģ afà i la funciÃģ quadrÃĄtica. Funcions racionals f(x) = A(x) B(x)
- 5. Funcions irracionals Funcions SÃģn funcions on no totes les imatges sÃģn nombres racionals, perÃē sà reals Funcions definides a trossos
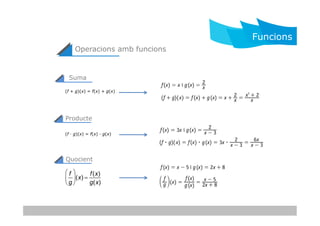
- 6. Operacions amb funcions (f + g)(x) = f(x) + g(x) Suma Funcions (f · g)(x) = f(x) · g(x) f g ÃĶ ÃĻ ç Ãķ Ãļ ÷(x) = f(x) g(x) Quocient Producte
- 7. Propietats de la suma de funcions Funcions Commutativa Associativa ExistÃĻncia dâelement neutre ExistÃĻncia dâelement simÃĻtric Propietats del producte de funcions Commutativa Associativa ExistÃĻncia dâelement neutre ExistÃĻncia dâelement simÃĻtric Distibutiva de la multiplicaciÃģ respecte de la suma
- 8. Funcions FunciÃģ composta g f (f composta amb g) com (g f) (x) = g [f(x)]. f g (g composta amb f) com (f g) (x) = f [g(x)]. ïŊ ïŊ ïŊ ïŊ Propietats Associativa ExistÃĻncia dâelement neutre ExistÃĻncia dâelement simÃĻtric
- 9. En la funciÃģ inversa, la variable independent de f passa a ser la variable dependent de f-1, i viceversa. FunciÃģ inversa Funcions CÃĄlcul de la funciÃģ inversa Expressar la variable y = f(x) en funciÃģ de la variable x. AÃŊllar la variable x de la igualtat anterior per tal de trobar lâexpressiÃģ de x en funciÃģ de y. Intercanviar les dues variables. Fer-ne la comprovaciÃģ.





![Funcions
FunciÃģ composta
g f (f composta amb g) com (g f) (x) = g [f(x)].
f g (g composta amb f) com (f g) (x) = f [g(x)].
ïŊ
ïŊ
ïŊ
ïŊ
Propietats
Associativa
ExistÃĻncia dâelement neutre
ExistÃĻncia dâelement simÃĻtric](https://image.slidesharecdn.com/u8-200822090745/85/Funcions-8-320.jpg)
