Fuzzy rough quickreduct algorithm
- 3. ? Find the Lower Approximation ? Find Fuzzy Positive Region ? Find Dependency Function
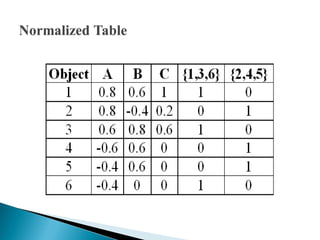
- 7. ? Decision attribute contains two equivalence classes U/Q = {{1,3,6}{2,4,5}} ? With those elements belonging to the class possessing a membership of one, otherwise zero ? Normalize the given Dataset (conditional attribute)
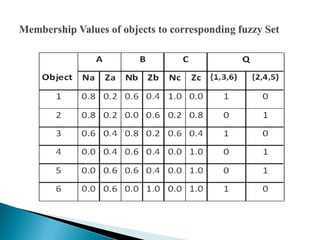
- 9. ? Using Normalized table, Calculate the values of N and Z. N = All Negative values change to Zero, Z = 1- ( Absolute Value of Normalized Table), ? Equivalence classes are ? U/A = {Na , Za} ? U/B = {Nb , Zb} ? U/C = {Nc , Zc} ? U/Q = {{1,3,6},{2,4,5}}
- 11. Here, F= Na, Za, Nb, Zb, Nc, Zc Inf - minimum Sup - maximum
- 13. min (0.8, inf {1,0.2,1,1,1,1}) = 0.2 min (0.8, inf {1,0.2,1,1,1,1}) = 0.2 min (0.6, inf {1,0.2,1,1,1,1}) = 0.2 min (0.2, inf {1,0.2,1,1,1,1}) = 0 min (0.2, inf {1,0.2,1,1,1,1}) = 0 min (0.2, inf {1,0.2,1,1,1,1}) = 0
- 14. max (0.8,1.0) = 1.0 max (0.8,0.0) = 0.8 max (0.6,1.0) = 1.0 max (0.6,0.0) = 0.6 max (0.4,0.0) = 0.4 max (0.4,1.0) = 1.0
- 15. min(0.2,inf {1,0.8,1,0.6,0.4,1}) = 0.2 min(0.2,inf {1,0.8,1,0.6,0.4,1}) = 0.2 min(0.4,inf {1,0.8,1,0.6,0.4,1}) = 0.4 min(0.4,inf {1,0.8,1,0.6,0.4,1}) = 0.4 min(0.6,inf {1,0.8,1,0.6,0.4,1}) = 0.4 min(0.6,inf {1,0.8,1,0.6,0.4,1}) = 0.4
- 16. (maximum)
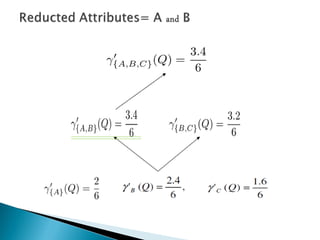
- 19. Similarly we find From this it can be seen that attribute B will cause the greatest increase in dependency degree.
- 20. Here, P = {A,B} U/A = {Na,Za} U/B = {Nb,Zb} U/P= U/A U/B = {Na,Za} {Nb,Zb} U/P = {Na ∩ Nb, Na ∩ Zb, Za ∩ Nb, Za ∩ Zb}
- 21. Similarly find Decision Table for, U/{B,C} ={Nb ∩ Nc, Nb ∩ Zc, Zb ∩ Nc, Zb ∩ Zc}, U/{A,B,C}= {(Na ∩ Nb ∩ Nc), (Na ∩ Nb ∩ Zc), (Na ∩ Zb ∩ Nc), (Na ∩ Zb ∩ Zc ), (Za ∩ Nb ∩ Nc), (Za ∩ Nb ∩ Zc), (Za ∩ Zb ∩ Nc), (Za ∩ Zb ∩ Zc)}
- 22. ? Find Dependency Degree, and,
- 24. ? As this causes no increase in dependency, the algorithm stops and outputs the reduct {A,B}. ? The dataset can now be reduced to only those attributes appearing in the reduct.