G T5 Resources Similarity Study Material.pptx
- 2. Vocabulary
- 3. Choose 3-4 vocabulary words for the day. Throughout the lesson, as students respond to your questions or are presenting a problem on the board, mark a tally when a vocabulary word is used accurately. This can be turned into a competition among groups or between periods. Mathematically Speaking! Examples of accuracy ŌĆó line vs line segment ŌĆó translation vs slide ŌĆó midpoint vs the middle
- 4. Betweenness ŌĆō given three points A, B, and C, B is between A and C if and only if all three of the points lie on the same line, and AB + BC = AC. A C B
- 5. CongruentŌĆō having the same size and shape, denoted by Ōēģ. ŌłåØÉ┤ØÉĄØÉČ Ōēģ ØÉĘØÉĖØÉ╣ ØÉ┤ØÉĄ Ōēģ ØÉČØÉĘ
- 6. Scale factor ŌĆō in a dilation, the ratio of a linear measurement of the image to the corresponding measurement of the preimage. Scale Factor = 9 3 = 3
- 7. Similar Figures ŌĆō figures with the same shape (but not necessarily the same size) and the following properties: ŌĆó Corresponding sides are proportional. That is, the ratios of the corresponding sides are equal. ŌĆó Corresponding angles are equal.
- 8. Similarity transformation ŌĆō a transformation that results in an image that is the same shape, but not necessarily the same size, as the original figure.
- 9. Dilation ŌĆō a transformation in which the lines connecting every point Øæā with its preimage ØæāŌĆÖ all intersect at a point ØÉ║ known as the center of dilation, and ØÉ║ØæāŌĆ▓ ØÉ║Øæā is the same for every point Øæā; a transformation that changes the size of a figure but not its shape. G
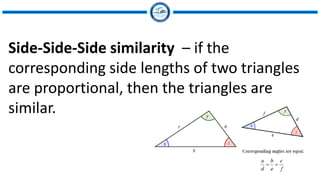
- 10. Side-Side-Side similarity ŌĆō if the corresponding side lengths of two triangles are proportional, then the triangles are similar.
- 11. Side-Angle-Side similarity ŌĆō if the lengths of two pairs of corresponding sides of two triangles are proportional and the angles the sides form are congruent, then the triangles are similar.
- 12. Angle-Angle similarity ŌĆō If two angles of one triangle are respectively equal to two angles of another triangle, then the two triangles are similar.
- 13. Side Splitter TheoremŌĆō If a line is parallel to a side of a triangle and intersect the other two sides, then this line divides those two sides proportionally. Øæ®Øæ┐ Øæ®Øæ© = Øæ®ØÆĆ Øæ®Øæ¬ = Øæ┐ØÆĆ Øæ©Øæ¬