![3.2. モデル作成 詳細は
【0/2】単位根検定 こちらを
趣旨：
このデータは、
Random Walk（乱数列）でないよね？
（Random Walk列でも、何かそれっぽいモデルが出来得る。
けど、そのモデルって一体何よ？ てな議論になるので…）
やり方：
「Random Walkではない」の仮説検定
? Phillips-Perron検定 [stats::PP.test]
? Augmented Dickey-Fuller検定 [tseries::adf.test]
2012/03/10 搁で骋础搁颁贬モデル 32](https://image.slidesharecdn.com/garchtokyor-120310012817-phpapp01/85/R-GARCH-TokyoR-21-32-320.jpg)
![3.2. モデル作成
【2/2】の前に fGarch::garchFit で最適次数の探索法
ループでコマンドを生成?実行し、listに投入、してみた。
（問題：(1) 係数発散時の問題 (２)エラー処理が未対応）
最適次数は、GARCH (1,1)
#書式: garchFit( ~ garch(P, Q), data = topix.return, trace = FALSE )
topix.garch <- as.list(NULL)
i <- 1; for (P in 1:5){ for (Q in 0:5){
topix.garch[[i]] <- try( eval( parse( text =
paste("garchFit( ~ garch(", P ,", ", Q , "), data = topix.return, trace = FALSE )" )
)), silent = TRUE)
i <- i + 1 } }
opt.topix.garch <-
Reduce(function(x,y) if(x@fit$ics[1] < y@fit$ics[1]){x} else{y}, topix.garch)
2012/03/10 搁で骋础搁颁贬モデル 36](https://image.slidesharecdn.com/garchtokyor-120310012817-phpapp01/85/R-GARCH-TokyoR-21-36-320.jpg)
![3.2. モデル作成
【参考】先のコードが汚い、Rらしくない、
とは思った、が改良は実力不足につき断念。
どうも、素直ではない書き方？をしないとダメっぽい。
library(fGarch)
spec <- garchSpec(model = list(alpha = 0.1, beta = c(0.4, 0.4)))
Xt <- garchSim(spec, n = 100)
x <- list()
for(q in 1:3){
print(q)
x[q] <- list(garchFit(substitute(~garch(1,beta), list(beta =q))
, data = Xt, trace = FALSE)) }
上記例：[R] fGarch: how to use garchFit() in loop?
https://stat.ethz.ch/pipermail/r-help/2010-August/249276.html
2012/03/10 搁で骋础搁颁贬モデル 37](https://image.slidesharecdn.com/garchtokyor-120310012817-phpapp01/85/R-GARCH-TokyoR-21-37-320.jpg)
![おまけ
何でこんな話をしたのか？
「月曜日にマーケットは動く（月曜日効果）」と聞くので。
? 理由の例：金曜→月曜だけ間隔が広く、情報が多く入るから
試しに：各曜日のTOPIXのリターンの標準偏差を計算
library(RFinanceYJ); library(xts)
# データを取得し、xtsに変換
topix.raw <- quoteStockTsData('998405.t‘
, since=‘2006-01-04’, date.end=‘2012-01-31’ )
topix.xts <- as.xts( read.zoo(topix.raw))
# 曜日毎の日次リターン?標準偏差の集計。1件目はNULLなので除外
tapply( ( (topix.xts[,4]-lag(topix.xts[,4]))-1 )[-1,]
, weekdays(index(topix.xts[-1,])) , sd)
2012/03/10 搁で骋础搁颁贬モデル 50](https://image.slidesharecdn.com/garchtokyor-120310012817-phpapp01/85/R-GARCH-TokyoR-21-50-320.jpg)
搁で骋础搁颁贬モデル - TokyoR #21
- 1. 搁で骋础搁颁贬モデル TokyoR #21 2012/03/10 @horihorio
- 2. 自己紹介 ? Twitter ID: @horihorio ? お仕事： データマイニング?コンサルタント （重要なこと：会社は非金融業） ただ何故か、金融機関の与信リスク管理? 分析を、4年少々やってたりする ? R使用歴： 半年もない、とか。前回発表（Tokyo.R#18: 「Rで学 ぶ 現代ポートフォリオ理論入門」 ）以降、程度 2012/03/10 搁で骋础搁颁贬モデル 2
- 3. ◇ 全体構成 ◇ 1. Executive Summary 2. 理論編 1. ARIMAモデル 2. GARCHモデル 3. 実践編 1. TOPIXとは？ 2. モデル作成 3. モデル検証 2012/03/10 搁で骋础搁颁贬モデル 3
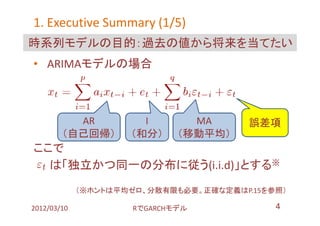
- 4. 1. Executive Summary (1/5) 時系列モデルの目的：過去の値から将来を当てたい ? ARIMAモデルの場合 AR I MA 誤差項 （自己回帰） （和分） （移動平均） ここで は「独立かつ同一の分布に従う(i.i.d)」とする※ （※ホントは平均ゼロ、分散有限も必要。正確な定義はP.15を参照） 2012/03/10 搁で骋础搁颁贬モデル 4
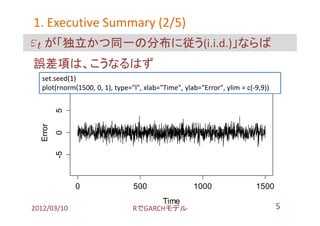
- 5. 1. Executive Summary (2/5) が「独立かつ同一の分布に従う(i.i.d.)」ならば 誤差項は、こうなるはず set.seed(1) plot(rnorm(1500, 0, 1), type="l", xlab="Time", ylab="Error", ylim = c(-9,9)) 5 Error 0 -5 0 500 1000 1500 Time 2012/03/10 搁で骋础搁颁贬モデル 5
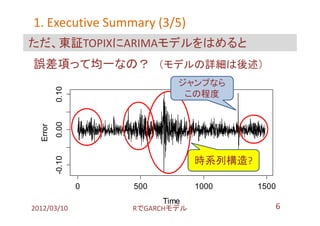
- 6. 1. Executive Summary (3/5) ただ、東証TOPIXにARIMAモデルをはめると 誤差項って均一なの？ （モデルの詳細は後述） ジャンプなら 0.10 この程度 0.00 Error 時系列構造? -0.10 0 500 1000 1500 Time 2012/03/10 搁で骋础搁颁贬モデル 6
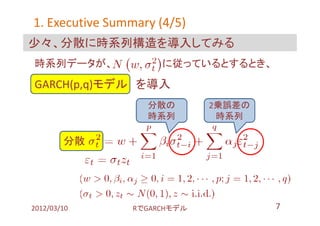
- 7. 1. Executive Summary (4/5) 少々、分散に時系列構造を導入してみる 時系列データが、 に従っているとするとき、 GARCH(p,q)モデル を導入 分散の 2乗誤差の 時系列 時系列 分散 １ 2012/03/10 搁で骋础搁颁贬モデル 7
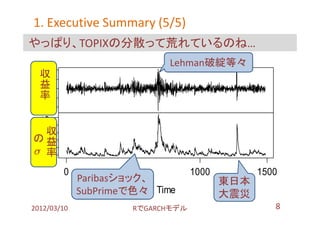
- 8. 1. Executive Summary (5/5) やっぱり、TOPIXの分散って荒れているのね… Lehman破綻等々 0.10 収 益 率 -0.10 0.05 収 の益 0.01 率 0 500 1000 1500 Paribasショック、 東日本 SubPrimeで色々 Time 大震災 2012/03/10 搁で骋础搁颁贬モデル 8
- 9. ◇ 全体構成 ◇ 1. Executive Summary 2. 理論編 1. ARIMAモデル 2. GARCHモデル 3. 実践編 1. TOPIXとは？ 2. モデル作成 3. モデル検証 2012/03/10 搁で骋础搁颁贬モデル 9
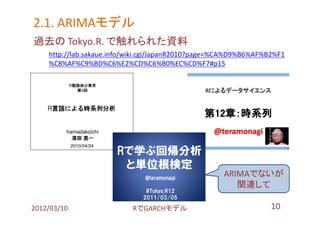
- 10. 2.1. ARIMAモデル ARIMAモデル 過去の Tokyo.R. で触れられた資料 http://lab.sakaue.info/wiki.cgi/JapanR2010?page=%CA%D9%B6%AF%B2%F1 %C8%AF%C9%BD%C6%E2%CD%C6%B0%EC%CD%F7#p15 ARIMAでないが 関連して 2012/03/10 搁で骋础搁颁贬モデル 10
- 11. 2.1. ARIMAモデル ARIMAモデル 時系列ARIMAモデルは、以下3要素からなる ? AR(Auto Regression)：自己回帰 → 過去の自分の値 ? I(Integrated)：和分 → 時系列データの階差をとる ? MA(Moving Average)：移動平均 → 現在および過去の誤差項の線型結合 ARIMA (Box-Jenkins) モデル AR I MA （自己回帰） （和分） （移動平均） 2012/03/10 搁で骋础搁颁贬モデル 11
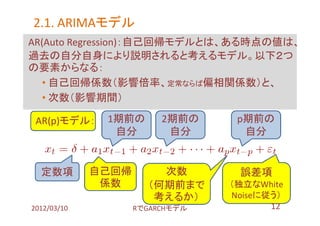
- 12. 2.1. ARIMAモデル ARIMAモデル AR(Auto Regression)：自己回帰モデルとは、ある時点の値は、 過去の自分自身により説明されると考えるモデル。以下２つ の要素からなる： ? 自己回帰係数（影響倍率、定常ならば偏相関係数）と、 ? 次数（影響期間） AR(p)モデル： 1期前の 2期前の p期前の 自分 自分 自分 定数項 自己回帰 次数 誤差項 係数 （何期前まで （独立なWhite 考えるか） Noiseに従う） 2012/03/10 搁で骋础搁颁贬モデル 12
- 13. 2.1. ARIMAモデル ARIMAモデル MA(Moving Average)：移動平均モデルとは、現在値と、過去 の誤差項の線形結合により表される関数 MA(q)モデル： 1期前の 2期前の q期前の 当期の誤差 誤差 誤差 誤差 MAモデルの意味って何よ？ ? 定常時系列ならば、AR(∞) = MA(t) ? つまり、「小さいAR項×沢山」が、MA項少々で済む 【イメージ】 0.8 MA(1) = 0.001 AR(101) + 0.0002 AR(102) + … 2012/03/10 搁で骋础搁颁贬モデル 13
- 14. 2.1. ARIMAモデル ARIMAモデル I(Integrated) ：和分とは、階差数列に対応する概念。 時系列モデルは、平均や自己共分散が一定（定常時系列） でないと扱えない。非定常→定常 の変換に使ったりする 現系列 階差数列 に対し 数列では 時系列では の一般項を求め のARMAモデルを推定し 2012/03/10 搁で骋础搁颁贬モデル 14
- 15. 2.1. ARIMAモデル ARIMAモデル AR + I + MA → ARIMAモデル が完成 ARIMAモデル AR I MA 誤差項 （自己回帰） （和分） （移動平均） ここで は、以下を満たす（分散均一性）： 2012/03/10 搁で骋础搁颁贬モデル 15
- 16. ◇ 全体構成 ◇ 1. Executive Summary 2. 理論編 1. ARIMAモデル 2. GARCHモデル 3. 実践編 1. TOPIXとは？ 2. モデル作成 3. モデル検証 2012/03/10 搁で骋础搁颁贬モデル 16
- 17. 2.2. GARCHモデル GARCHモデル ARIMAモデルが弱い例 ? 金融市場：概して、荒れた翌日の値動きは活発 ? 2ch：祭りが起きた後は、暫く高アクセスが続く？ つまり、 ? 突発的な変動と、その後の「荒れ」が続き、 誤差項が「独立かつ同一の分布」でない と弱い 対策 GARCHモデル ? 分散にも時系列構造を導入 ※GARCH: Generalized AutoRegressive Conditional Heteroskedasticity 2012/03/10 搁で骋础搁颁贬モデル 17
- 18. 2.2. GARCHモデル GARCHモデル 【参考】周期変動ならば、Seasonal ARIMAが素直 例： は4半期データ（周期4）とする。 ここで、4期前との差分 を考える。 そして、 と でARIMAモデルを構築して掛け算。 Rでの使用例 arima(UKgas, order=c(2,1,2), seasonal=list(order=c(1,1,3), period=4 ) 2012/03/10 搁で骋础搁颁贬モデル 18
- 19. 2.2. GARCHモデル GARCHモデル GARCH(p,q)モデルの式 時系列データが、 に従っているとするとき、 分散の 2乗誤差の 時系列 時系列 分散 １ ただし、 防止が目的 、 、 、 、 、 2012/03/10 搁で骋础搁颁贬モデル 19
- 20. 2.2. GARCHモデル GARCHモデル 【参考】2乗誤差のみ考える、ARCH(q)モデルもある。 要は、GARCHモデルで としたもの。 時系列データが、 に従っているとするとき、 2乗誤差の 分散 １ 時系列 ただし、 、 、 、 、 ※ARCH: AutoRegressive Conditional Heteroskedasticity 2012/03/10 搁で骋础搁颁贬モデル 20
- 21. 2.2. GARCHモデル GARCHモデル 【参考】もっともな懸念で… データが常に正規分布ではない。最後の分散の誤差が になる訳ないのでは？ 【答え】 ? 正規分布以外では、GARCHアルゴリズムの最尤推 定量は間違っている ? ただ、標本数が大だと、最尤法の一致性ならOK ? よって、実際の分布は正規分布でないが、正規分 布のGARCH推定量でいいや、と割り切る？ ? ただ、最尤推定量や、（尤度を用いる）AIC等の情報 量基準は、全て「擬似的な値」、なのは留意 2012/03/10 搁で骋础搁颁贬モデル 21
- 22. 2.2. GARCHモデル GARCHモデル GARCHモデルへのケチ： 制約ナシだと となるのは、何かと不自由 改良例 EGARCH(p,q)モデル 係数の制約：ナシ！ 2012/03/10 搁で骋础搁颁贬モデル 22
- 23. 2.2. GARCHモデル GARCHモデル EGARCHモデルって 【嬉しいこと】 ? 左辺は対数なので、右辺が負でも対応可能 ? 負になる変数でも、モデルに投入可能 【嬉しくないこと】 ? Rではどうやって扱うの？が不明… ? CRANで egarch::egarch は発見したが、何か大丈 夫？ってな香りがしたので自粛。Predictがダメ。 （だし、時間がなかった。） ? （緩募）egarchは大丈夫か否か、他にRでEGARCHモ デルを適用出来る方法、等々 2012/03/10 搁で骋础搁颁贬モデル 23
- 24. 2.2. GARCHモデル GARCHモデル その他、GARCHの拡張例 負ならば1となるダミー ? GJR(p,q)モデル ? Absolute Residual モデル ? 他に、Non-Linear GARCH, Quadratic GARCH, Threshold GARCH 等があり 2012/03/10 搁で骋础搁颁贬モデル 24
- 25. ◇ 全体構成 ◇ 1. Executive Summary 2. 理論編 1. ARIMAモデル 2. GARCHモデル 3. 実践編 1. TOPIXとは？ 2. モデル作成 3. モデル検証 2012/03/10 搁で骋础搁颁贬モデル 25
- 26. 3.0. 以下のアウトライン 東証TOPIX（後述）の、対前日比リターンに 1. ARIMAモデル （季節調整なし） 2. ARMAモデル + GARCHモデル を当てはめ、比較してゆく。 モデル構築期間： 2006/1/4～2012/1/31 （N=1489） モデル検証期間： 2012/2/1～2012/3/10 （N=28） 2012/03/10 搁で骋础搁颁贬モデル 26
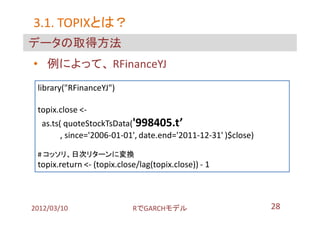
- 27. 3.1. TOPIXとは？ TOPIXとは？ 東証1部全体の時価総額を指標化した値 野村證券?証券用語解説集より 東京証券取引所が日々計算し発表している株価指数で、 東証第1部の毎日の時価総額（全上場株をある日の終値 で評価したものの合計額）を基準日の時価総額で割って 算出される。 1968(昭和43)年1月4日の時価総額を100として計算して おり、日経平均株価とならんで、重要な指数の1つとなっ ている。 引用元：http://www.nomura.co.jp/terms/japan/to/topix.html 2012/03/10 搁で骋础搁颁贬モデル 27
- 28. 3.1. TOPIXとは？ TOPIXとは？ データの取得方法 ? 例によって、 RFinanceYJ library("RFinanceYJ") topix.close <- as.ts( quoteStockTsData('998405.t’ , since='2006-01-01', date.end='2011-12-31' )$close) # コッソリ、日次リターンに変換 topix.return <- (topix.close/lag(topix.close)) - 1 2012/03/10 搁で骋础搁颁贬モデル 28
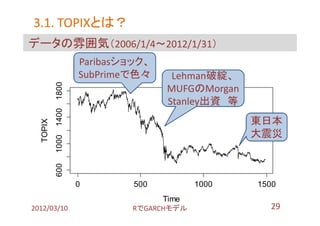
- 29. 3.1. TOPIXとは？ TOPIXとは？ データの雰囲気（2006/1/4～2012/1/31） Paribasショック、 SubPrimeで色々 Lehman破綻、 1800 MUFGのMorgan Stanley出資 等 1400 東日本 TOPIX 大震災 1000 600 0 500 1000 1500 Time 2012/03/10 搁で骋础搁颁贬モデル 29
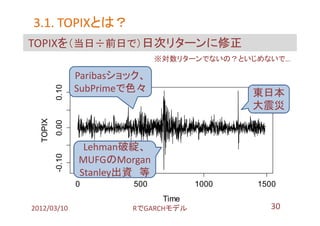
- 30. 3.1. TOPIXとは？ TOPIXとは？ TOPIXを（当日÷前日で）日次リターンに修正 ※対数リターンでないの？といじめないで… Paribasショック、 SubPrimeで色々 0.10 東日本 大震災 TOPIX 0.00 Lehman破綻、 -0.10 MUFGのMorgan Stanley出資 等 0 500 1000 1500 Time 2012/03/10 搁で骋础搁颁贬モデル 30
- 31. ◇ 全体構成 ◇ 1. Executive Summary 2. 理論編 1. ARIMAモデル 2. GARCHモデル 3. 実践編 1. TOPIXとは？ 2. モデル作成 3. モデル検証 2012/03/10 搁で骋础搁颁贬モデル 31
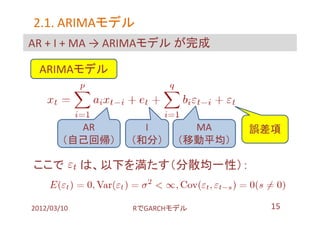
- 32. 3.2. モデル作成 詳細は 【0/2】単位根検定 こちらを 趣旨： このデータは、 Random Walk（乱数列）でないよね？ （Random Walk列でも、何かそれっぽいモデルが出来得る。 けど、そのモデルって一体何よ？ てな議論になるので…） やり方： 「Random Walkではない」の仮説検定 ? Phillips-Perron検定 [stats::PP.test] ? Augmented Dickey-Fuller検定 [tseries::adf.test] 2012/03/10 搁で骋础搁颁贬モデル 32
- 33. 3.2. モデル作成 確認してみる(PP.testを使用) > PP.test(topix.close) # TOPIX現系列 Random Walkの Phillips-Perron Unit Root Test 可能性61% data: topix.close Dickey-Fuller = -1.9303, Truncation lag parameter = 7, p-value = 0.6078 Random Walkの > PP.test(topix.return) # TOPIXリターン系列 可能性1% Phillips-Perron Unit Root Test data: topix.return Dickey-Fuller = -39.3825, Truncation lag parameter = 7, p-value = 0.01 よって、安心してリターン系列はいじれる。 2012/03/10 搁で骋础搁颁贬モデル 33
- 34. 3.2. モデル作成 【1/2】（季節調整なし）ARIMAモデル 参考：Tokyo.R#17 @teramonagi さん資料 （ただ、問題があるのだが…。次のスライドで） 最適次数は、ARIMA = (4,0,4) library("snow") hosts <- rep("localhost", 2) cl <- makeCluster(hosts, type=“SOCK”); clusterExport(cl, "topix.return") clusterCall(cl,topix.arima <- apply(expand.grid(1:5,1,0:5) , 1 , function(x) { try( arima(topix.return, order = x ) , TRUE) } ) ) stopCluster(cl) opt.topix.arima <- Reduce(function(x,y) if(x$aic < y$aic){x} else{y}, topix.arima) 2012/03/10 搁で骋础搁颁贬モデル 34
- 35. 3.2. モデル作成 【参考】前ページの問題：係数が収束しない場合 ARIMA = (3,1,5) は、一部係数が無限大に飛ぶ 係数は∞ fixed=c(0,NA,NA,0,0,NA,NA,NA)) arima(topix.return,order = c(3,1,5), で無限大の項を除去できるが、当然AICの値は変わる 2012/03/10 搁で骋础搁颁贬モデル 35
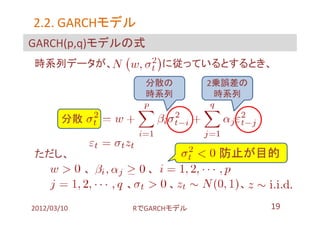
- 36. 3.2. モデル作成 【2/2】の前に fGarch::garchFit で最適次数の探索法 ループでコマンドを生成?実行し、listに投入、してみた。 （問題：(1) 係数発散時の問題 (２)エラー処理が未対応） 最適次数は、GARCH (1,1) #書式: garchFit( ~ garch(P, Q), data = topix.return, trace = FALSE ) topix.garch <- as.list(NULL) i <- 1; for (P in 1:5){ for (Q in 0:5){ topix.garch[[i]] <- try( eval( parse( text = paste("garchFit( ~ garch(", P ,", ", Q , "), data = topix.return, trace = FALSE )" ) )), silent = TRUE) i <- i + 1 } } opt.topix.garch <- Reduce(function(x,y) if(x@fit$ics[1] < y@fit$ics[1]){x} else{y}, topix.garch) 2012/03/10 搁で骋础搁颁贬モデル 36
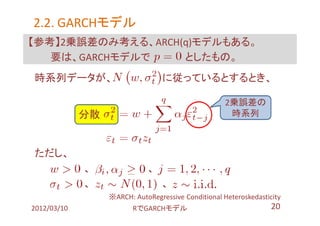
- 37. 3.2. モデル作成 【参考】先のコードが汚い、Rらしくない、 とは思った、が改良は実力不足につき断念。 どうも、素直ではない書き方？をしないとダメっぽい。 library(fGarch) spec <- garchSpec(model = list(alpha = 0.1, beta = c(0.4, 0.4))) Xt <- garchSim(spec, n = 100) x <- list() for(q in 1:3){ print(q) x[q] <- list(garchFit(substitute(~garch(1,beta), list(beta =q)) , data = Xt, trace = FALSE)) } 上記例：[R] fGarch: how to use garchFit() in loop? https://stat.ethz.ch/pipermail/r-help/2010-August/249276.html 2012/03/10 搁で骋础搁颁贬モデル 37
- 38. 3.2. モデル作成 【2/2】ARMAモデル + GARCHモデル データは だと仮定して、 ? （条件付き）平均値はARMAにて ? （条件付き）分散はGARCHにて推定 ただ、これも係数発散問題が発生した… （最後は怪しい手作業の）探索結果は、ARMA(5, 5) + GARCH(1, 1) #書式: garchFit( ~ arma(p, q) + garch(P, Q) , data = topix.return, trace = FALSE ) やったソース：先のGARCHモデル のノリで、もっと醜悪にしたもの… 実行には3?4時間くらいかかった、気がする。 2012/03/10 搁で骋础搁颁贬モデル 38
- 39. ◇ 全体構成 ◇ 1. Executive Summary 2. 理論編 1. ARIMAモデル 2. GARCHモデル 3. 実践編 1. TOPIXとは？ 2. モデル作成 3. モデル検証 2012/03/10 搁で骋础搁颁贬モデル 39
- 40. 3.3. モデル検証 最初にお詫び 以降のモデル検証は、 ? 前節でのエラーが取り切れていない ? だからか？GARCHモデルの検証結果が怪しい ? （あと時間不足で）モデルの予測まで未到達 です。何卒、ご了承下さい…。 2012/03/10 搁で骋础搁颁贬モデル 40
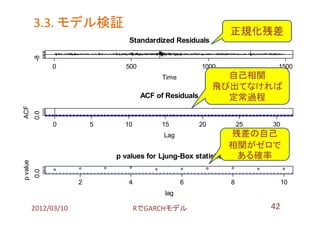
- 41. 3.3. モデル検証 【1/2】ARIMAモデルの場合 stats::tsdiag で残差を見てゆく。 ? 使用例： tsdiag(opt.topix.arima, gof.lag=10 ) （※ gof.lagは、最下段：残差の自己相関 の検定時のラグ数） ? 出力例は、次のページで。 結果：とりあえず、問題なさそうな。 2012/03/10 搁で骋础搁颁贬モデル 41
- 42. 3.3. モデル検証 正規化残差 -8 Standardized Residuals 0 500 1000 1500 Time 自己相関 飛び出てなければ ACF of Residuals 定常過程 ACF 0.0 0 5 10 15 20 25 30 Lag 残差の自己 相関がゼロで p values for Ljung-Box statistic ある確率 p value 0.0 2 4 6 8 10 lag 2012/03/10 搁で骋础搁颁贬モデル 42
- 43. 3.3. モデル検証 【2/2】ARMA + GARCHモデルの場合 見たい事： ? 基準化された残差 はゼロなの？ ? 基準化された残差 は正規分布なの？ 再掲： を仮定して GARCHモデル 但し、 、 2012/03/10 搁で骋础搁颁贬モデル 43
- 44. 3.3. モデル検証 【2/2】GARCHモデルの場合 収束がどうも怪しい 左：残差の平均 右：平均値の標準誤差 正規分布テストもダメ 平均ゼロで無い！orz 尖度?歪度を見た （要Package: e1071） 2012/03/10 搁で骋础搁颁贬モデル 44
- 45. 3.3. モデル検証 ARIMAとGARCHモデルの比較 やりたかったこと（その１） ? GARCHモデルで、 は の不偏推定量なのか？ 具体的には、 誤差項 の回帰式を考える。 もし不偏推定量ならば、 係数が になるハズ。 2012/03/10 搁で骋础搁颁贬モデル 45
- 46. 3.3. モデル検証 ARIMAとGARCHモデルの比較 やりたかったこと（その２） ? GARCHモデルを導入すると、ARIMAモデルより「美味し い」のか？の検証 ? 但し、ある指標で決まる話ではない。予測するものは、 ARIMAモデル：出力は時系列の値 GARCHモデル：出力は分散の値 と異なるため。 ? 考えていた観点の例： ? ARIMAでの予測標準誤差を、GARCHの値と比較 ? （特に荒れたときの）過去時点での予測値を比較 2012/03/10 搁で骋础搁颁贬モデル 46
- 47. まとめ ? 時系列モデルとは、過去の値から将来の値を予測するモ デルで、代表的なものにARIMAモデルがある。 ? ARIMAモデルは、残差の分散が均一なのを仮定。よって、 突発的な変動があると弱い ? GARCHモデルは、残差に時系列構造を導入することで、突 発的な変動にも対応しようとするモデル 今後の課題 ? モデルの係数が発散する場合の対応（参考：P35） ? （↑ に関連し）ホントは、係数推定前にエラー検知したい 2012/03/10 搁で骋础搁颁贬モデル 47
- 48. おまけ 最近買った本（参考文献４）を眺めていて 観測時系列データ： は、必ずしも等時間間隔で取得できるとは限らない。 そこで、連続時間の確率過程を↓と表記 間隔が開くと、分散が大 ここで、 は標準ウィナー過程であり、 は平均ゼロ、分散 に従う。 2012/03/10 搁で骋础搁颁贬モデル 48
- 49. おまけ （平均回帰する）具体的なモデルの一例： ? Ornstein-Uhlenbeck過程（OU過程） （ のときにErgotic（何かに確率収束する）） ? Vasicek過程 （ のときにErgotic） 2012/03/10 搁で骋础搁颁贬モデル 49
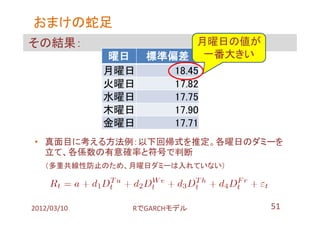
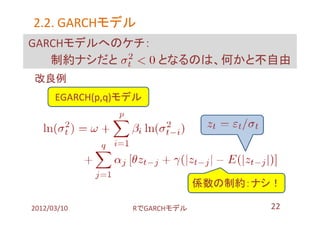
- 50. おまけ 何でこんな話をしたのか？ 「月曜日にマーケットは動く（月曜日効果）」と聞くので。 ? 理由の例：金曜→月曜だけ間隔が広く、情報が多く入るから 試しに：各曜日のTOPIXのリターンの標準偏差を計算 library(RFinanceYJ); library(xts) # データを取得し、xtsに変換 topix.raw <- quoteStockTsData('998405.t‘ , since=‘2006-01-04’, date.end=‘2012-01-31’ ) topix.xts <- as.xts( read.zoo(topix.raw)) # 曜日毎の日次リターン?標準偏差の集計。1件目はNULLなので除外 tapply( ( (topix.xts[,4]-lag(topix.xts[,4]))-1 )[-1,] , weekdays(index(topix.xts[-1,])) , sd) 2012/03/10 搁で骋础搁颁贬モデル 50
- 51. おまけの蛇足 その結果： 月曜日の値が 曜日 標準偏差 一番大きい 月曜日 18.45 火曜日 17.82 水曜日 17.75 木曜日 17.90 金曜日 17.71 ? 真面目に考える方法例：以下回帰式を推定。各曜日のダミーを 立て、各係数の有意確率と符号で判断 （多重共線性防止のため、月曜日ダミーは入れていない） 2012/03/10 搁で骋础搁颁贬モデル 51
- 52. 参考文献 1. 渡部敏明 『ボラティリティ変動モデル』 朝倉書店 2000年 2. 岡田昌史（代表） 『Rパッケージガイドブック』 東京書籍 2011年 ? 特に高柳氏のRmetricsのところを参照 3. P. Teetor（著）大橋?木下（訳）『Rクックブック』 オライリー?ジャパン 2011年 4. 西山陽一 『ISMシリーズ：進化する統計数理1 マルチンゲー ル理論による統計解析』 近代科学社 2011年 2012/03/10 搁で骋础搁颁贬モデル 52