Geo trans
- 1. Geometri Transformasi Yulian Sari, M.Si UNRIKA (Institute) Relasi dan Fungsi 1 / 10
- 2. Geometri Transformasi Silabus Perkuliahan Relasi, Fungsi, dan Transformasi (Institute) Relasi dan Fungsi 2 / 10
- 3. Geometri Transformasi Silabus Perkuliahan Relasi, Fungsi, dan Transformasi Isometri dan Pencerminan (Institute) Relasi dan Fungsi 2 / 10
- 4. Geometri Transformasi Silabus Perkuliahan Relasi, Fungsi, dan Transformasi Isometri dan Pencerminan Setengah Putaran dan Ruas Garis Berarah (Institute) Relasi dan Fungsi 2 / 10
- 5. Geometri Transformasi Silabus Perkuliahan Relasi, Fungsi, dan Transformasi Isometri dan Pencerminan Setengah Putaran dan Ruas Garis Berarah Translasi (Institute) Relasi dan Fungsi 2 / 10
- 6. Geometri Transformasi Silabus Perkuliahan Relasi, Fungsi, dan Transformasi Isometri dan Pencerminan Setengah Putaran dan Ruas Garis Berarah Translasi Translasi (Institute) Relasi dan Fungsi 2 / 10
- 7. Geometri Transformasi Silabus Perkuliahan Relasi, Fungsi, dan Transformasi Isometri dan Pencerminan Setengah Putaran dan Ruas Garis Berarah Translasi Translasi Ketertutupan Translasi (Institute) Relasi dan Fungsi 2 / 10
- 8. Geometri Transformasi Silabus Perkuliahan Relasi, Fungsi, dan Transformasi Isometri dan Pencerminan Setengah Putaran dan Ruas Garis Berarah Translasi Translasi Ketertutupan Translasi Rotasi (Institute) Relasi dan Fungsi 2 / 10
- 9. Geometri Transformasi Silabus Perkuliahan Relasi, Fungsi, dan Transformasi Isometri dan Pencerminan Setengah Putaran dan Ruas Garis Berarah Translasi Translasi Ketertutupan Translasi Rotasi Rotasi (Institute) Relasi dan Fungsi 2 / 10
- 10. Geometri Transformasi Silabus Perkuliahan Relasi, Fungsi, dan Transformasi Isometri dan Pencerminan Setengah Putaran dan Ruas Garis Berarah Translasi Translasi Ketertutupan Translasi Rotasi Rotasi Komposisi Rotasi (Institute) Relasi dan Fungsi 2 / 10
- 11. Geometri Transformasi Silabus Perkuliahan Relasi, Fungsi, dan Transformasi Isometri dan Pencerminan Setengah Putaran dan Ruas Garis Berarah Translasi Translasi Ketertutupan Translasi Rotasi Rotasi Komposisi Rotasi ReŌĆĪeksi Geser dan Grup Isometri (Institute) Relasi dan Fungsi 2 / 10
- 12. Geometri Transformasi Silabus Perkuliahan Relasi, Fungsi, dan Transformasi Isometri dan Pencerminan Setengah Putaran dan Ruas Garis Berarah Translasi Translasi Ketertutupan Translasi Rotasi Rotasi Komposisi Rotasi ReŌĆĪeksi Geser dan Grup Isometri Teorema Dasar Isometri (Institute) Relasi dan Fungsi 2 / 10
- 13. Geometri Transformasi Silabus Perkuliahan Relasi, Fungsi, dan Transformasi Isometri dan Pencerminan Setengah Putaran dan Ruas Garis Berarah Translasi Translasi Ketertutupan Translasi Rotasi Rotasi Komposisi Rotasi ReŌĆĪeksi Geser dan Grup Isometri Teorema Dasar Isometri Similaritas (Institute) Relasi dan Fungsi 2 / 10
- 14. Geometri Transformasi Silabus Perkuliahan Relasi, Fungsi, dan Transformasi Isometri dan Pencerminan Setengah Putaran dan Ruas Garis Berarah Translasi Translasi Ketertutupan Translasi Rotasi Rotasi Komposisi Rotasi ReŌĆĪeksi Geser dan Grup Isometri Teorema Dasar Isometri Similaritas Similaritas dan Dilatasi (Institute) Relasi dan Fungsi 2 / 10
- 15. Relasi DeŌĆ”nition Misalkan A dan B dua himpunan tak kosong dan P(x, y) kalimat matematika terbuka. Relasi R dari himpunan A dan B merupakan suatu himpunan yang anggota-anggotanya adalah pasangan terurut (a, b) dengan a 2 A dan b 2 B dan P(a, b) bernilai benar (Institute) Relasi dan Fungsi 3 / 10
- 16. Beberapa Istilah dalam Relasi Misalkan R relasi dari himpunan A ke B. Apabila x 2 A, maka peta dari x oleh relasi R adalah semua y 2 B sehingga (x, y) 2 R (Institute) Relasi dan Fungsi 4 / 10
- 17. Beberapa Istilah dalam Relasi Misalkan R relasi dari himpunan A ke B. Apabila x 2 A, maka peta dari x oleh relasi R adalah semua y 2 B sehingga (x, y) 2 R Apabila y 2 B, maka prapeta dari y oleh relasi R adalah semua x 2 A sehingga (x, y) 2 R yang disebut domain dari R (Institute) Relasi dan Fungsi 4 / 10
- 18. Beberapa Istilah dalam Relasi Misalkan R relasi dari himpunan A ke B. Apabila x 2 A, maka peta dari x oleh relasi R adalah semua y 2 B sehingga (x, y) 2 R Apabila y 2 B, maka prapeta dari y oleh relasi R adalah semua x 2 A sehingga (x, y) 2 R yang disebut domain dari R Himpunan yang terdiri dari semua y 2 B sehingga (x, y) 2 R disebut range dari R (Institute) Relasi dan Fungsi 4 / 10
- 19. Macam-macam Relasi (1) DeŌĆ”nition Misalkan A suatu himpunan himpunan tak kosong, R suatu relasi dari A ke A. R disebut relasi reŌĆĪeksi jika dan hanya jika untuk setiap x 2 A berlaku (x, x) 2 R. Example Misalkan A = f1, 2, 3, 4g dengan R1 = f(1, 1), (2, 4), (4, 1), (4, 4)g, R2 = f(1, 1), (2, 2), (3, 3), (4, 4)g. R1 bukan relasi reŌĆĪeksi sebab 2, 3 2 A sedangkan (2, 2), (3, 3) /2 R1, tetapi R2 adalah relasi reŌĆĪeksi sebab untuk setiap x 2 A, maka (x, x) 2 R2. (Institute) Relasi dan Fungsi 5 / 10
- 20. Macam-macam Relasi (2) DeŌĆ”nition Misalkan A suatu himpunan himpunan tak kosong, R suatu relasi pada A (dari A ke A). R disebut relasi simetri jika dan hanya jika untuk setiap (x, y) 2 R berlaku (y, x) 2 R. Example R1dan R2 pada contoh sebelumnya, masing-masing bukan merupakan relasi simetri, sebab (2, 4) 2 R1, tetapi (4, 2) /2 R1 dan (4, 1) 2 R2 tetapi (1, 4) /2 R2. (Institute) Relasi dan Fungsi 6 / 10
- 21. Macam-macam Relasi (3) DeŌĆ”nition Misalkan A suatu himpunan himpunan tak kosong, R suatu relasi pada A (dari A ke A). R disebut relasi transitif jika dan hanya jika untuk setiap (x, y), (y, z) 2 R berlaku (x, z) 2 R. Example Misalkan A = f1, 2, 3, 4g dengan R1,R2, R3 = f(1, 2), (2, 1)g, R4 = f(1, 1), (2, 2), (3, 3), (4, 4)g. R1 dan R3 bukan merupakan relasi transitif sebab (2, 4), (4, 1) 2 R1, tetapi (2, 1) /2 R1, sedangkan (1, 2), (2, 1) 2 R3, tetapi (1, 1) /2 R3. (Institute) Relasi dan Fungsi 7 / 10
- 22. Macam-macam Relasi (4) DeŌĆ”nition Misalkan A suatu himpunan himpunan tak kosong, R suatu relasi pada A (dari A ke A). R disebut relasi ekuivalen jika dan hanya jika R adalah relasi reŌĆĪeksi, simetri, dan transitif. Example Misalkan A = f1, 2, 3, 4g dengan R3 = f(1, 2), (2, 1)g, R4 = f(1, 1), (2, 2), (3, 3), (4, 4)g. Masing-masing untuk setiap (x, y) 2 R3, maka (y, x) 2 R3, dan untuk setiap (x, y) 2 R4, maka (y, x) 2 R4 dalam hal in x = y. (Institute) Relasi dan Fungsi 8 / 10
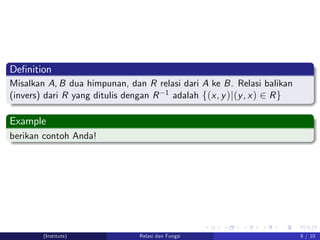
- 23. DeŌĆ”nition Misalkan A, B dua himpunan, dan R relasi dari A ke B. Relasi balikan (invers) dari R yang ditulis dengan R 1 adalah f(x, y)j(y, x) 2 Rg Example berikan contoh Anda! (Institute) Relasi dan Fungsi 9 / 10
- 24. Fungsi DeŌĆ”nition Suatu relasi f dari himpunan A ke B jika dan hanya jika setiap x 2 A ada dengan tunggal y 2 B sehingga (x, y) 2 f . Example Misalkan R himpunan semua bilangan rill. Dimisalkan relasi f dari R ke R sebagai berikut. Kemudian tentukan manakah relasi tersebut yang merupakan fungsi. 1 f (x) = 1 x+1 , 8x 2 R 2 f (x) = x2, 8x 2 R 3 f (x) = x3, 8x 2 R (Institute) Relasi dan Fungsi 10 / 10