Gerbang gerbang dasar logika
Download as PPTX, PDF
1 like3,361 views
Dokumen ini membahas tentang gerbang logika dasar seperti AND, OR, dan NOT. Termasuk definisi operasi masing-masing gerbang, persamaan aljabar Boolean, dan tabel kebenaran. Juga dijelaskan teorema-teorema dasar aljabar Boolean yang digunakan untuk mengolah dan meminimumkan persamaan logika.
Gerbang gerbang dasar logika
- 2. Siswa dapat menjelaskan operasi berbagai gerbang dasar Siswa dapat menjelaskan persamaan Aljabar Boole untuk berbagai gerbang dasar Siswa dapat membuat Tabel Kebenaran (Truth Table) untuk berbagai gerbang dasar
- 3. Gerbang logika merupakan dasar pembentukan sistem digital. Gerbang logika beroperasi dengan bilangan biner, sehingga disebut juga gerbang logika biner. Tegangan yang digunakan dalam gerbang logika adalah TINGGI (High) atau RENDAH (Low). Tegangan tinggi berarti 1, sedangkan tegangan rendah berarti 0. gerbang dasar logika terdiri dari: Gerbang AND Gerbang OR Gerbang NOT
- 4. Gerbang AND didefinisikan sebagai gerbang logika yang memberikan keadaan level logika 1 pada outputnya, jika semua keadaan inputnya berlevel logika 1 (tinggi).
- 5. A B C 0 0 0 0 1 0 1 0 0 1 1 1
- 7. Gerbang OR didefinisikan sebagai gerbang logika yang memberikan keadaan logika 1 (tinggi) pada outputnya, jika keadaan salah satu atau lebih inputnya berlogika 1 (tinggi).
- 8. A B C 0 0 0 0 1 1 1 0 1 1 1 1 OrGateTabel.swf
- 10. NOT merupakan gerbang logika yang memberikan keadaan level logika 1 pada outputnya, jika keadaan outputnya berlevel logika 0 atau sebaliknya.
- 11. A Y 0 1 1 0
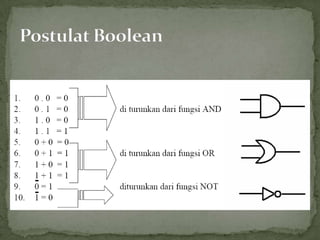
- 14. Tabel di bawah menunjukkan teorem asas Aljabar Boolean yang akan digunakan untuk mengolah dan meminimumkan persamaan.
- 15. Dua peraturan yang pertama untuk setiap logika menunjukkan bahawa persamaan di sebelah kiri adalah sama dengan persamaan di sebelah kanan walaupun tertib operasi logiknya berbeza. Manakala persamaan ketiga menunjukkan bagaimana sesuatu persamaan boleh dipanjangkan atau difaktorkan.
- 16. No AND OR KETERANGAN 1 2 3 4 5 6 7 8 9 (A.B).C = A.(B.C) A .B = B .A (A+B).(A+C)=A+(B.C) A.O = O A.A = A A.A= O A = A A.O= O A .1 = A A.(A + B ) = A (A+B)+C=A+(B+C) A+B=B+A (A.B)+(A.C)=A(B+C) A+1= 1 A+A=A A+ A=1 A = A A + O = A A + 1 = 1 A + (A.B) = A Hk.Asosiatif Hk.Komutatif Hk.Distributif Hk.Identitas Hk.Idempoten Hk.Inversi/Negasi Hk.Negasi Ganda Hk.Hubungan Dgn Suatu Konstanta Hk.Absorbsi
- 17. Teorem ini menyatakan cara untuk memisahkan pelengkap pada sebutan panjang, yaitu sebutan yang mempunyai lebih dari satu pemboleh ubah. Dengan kata lain, teorem ini menghapuskan pelengkap sebutan dengan menyonsangkan setiap pemboleh ubah dan operator dalam sebutan tersebut.
- 18. Buktikan persamaan berikut menggunakan aljabar boolean atau tabel kebenaran
- 19. Gunakan persamaan boole untuk menyederhanakan persamaan berikut