�ݺ�ߣ

HISTORY
Introduced in the 1630s , an important
mathematical development, for it laid
the foundations for modern
mathematics as well as
Aided the development of calculus
RENE DESCARTES (1596-1650) and
PIERRE DE FERMAT (1601-1665),
French mathematicians,
independently developed
the foundations for
analytical geometry

ANALYTIC GEOMETRY
• A branch of mathematics which
uses algebraic equations to
describe the size and position
of geometric figures on a
coordinate system.

ANALYTIC GEOMETRY
• The link between algebra and
geometry was made possible by the
development of a coordinate system
which allowed geometric ideas, such
as point and line, to be described in
algebraic terms like real numbers
and equations.
• Also known as Cartesian geometry
or coordinate geometry.

ANALYTIC GEOMETRY
• The use of a coordinate system to relate
geometric points to real numbers is the
central idea of analytic geometry.
• By defining each point with a unique set
of real numbers, geometric figures such
as lines, circles, and conics can be
described with algebraic equations.

CARTESIAN PLANE
• The Cartesian plane, the basis of analytic
geometry, allows algebraic equations to be
graphically represented, in a process called
graphing.
• It is actually the graphical representation of
an algebraic equation, of any form -- graphs
of polynomials, rational functions, conic
sections, hyperbolas, exponential and
logarithmic functions, trigonometric functions,
and even vectors.

CARTESIAN PLANE
• x-axis (horizontal axis)
where the x values are
plotted along.
• y-axis (vertical axis)
where the y values are
plotted along.
• origin, symbolized by 0,
marks the value of 0 of
both axes
• coordinates are given
in the form (x,y) and is
used to represent
different points on the
plane.

INCLINATION OF A LINE
• The smallest angle θ, greater than
or equal to 0°, that the line makes
with the positive direction of the x-
axis (0° ≤ θ < 180°)
• Inclination of a horizontal line is 0.
• The tangent of the inclination
m = tan θ

INCLINATION OF A LINE
O M
θ
x
y
L
O M
θ
x
y
L

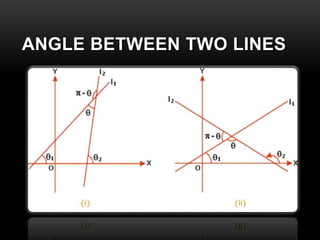
ANGLE BETWEEN TWO LINES
• If θ is angle, measured counter clockwise,
between two lines, then
• where m2 is the slope of the terminal side
and m1 is the slope of the initial side

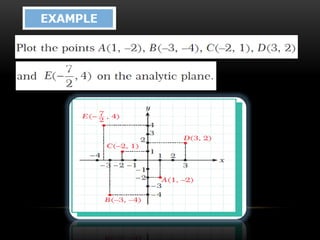
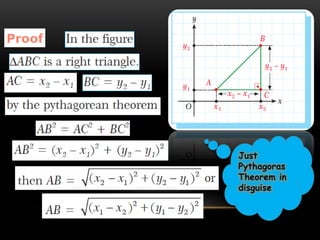
●A point is an ordered pair of numbers written as (x; y).
●Distance is a measure of the length between two points.
●The formula for finding the distance between any two points is:

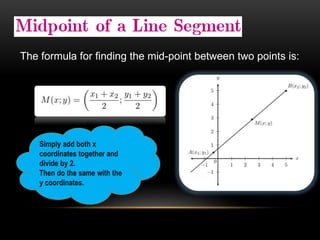
The formula for finding the mid-point between two points is:

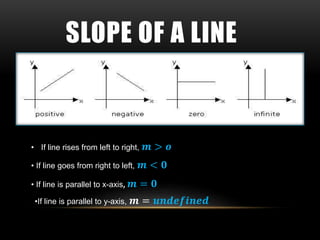
SLOPE OF A LINE
• The slope or gradient of a line describes the
steepness, incline or grade.
• A higher slope value indicates a steeper
incline.
• Slope is normally described by the ratio of the
“rise” divided by the “run” between two points
on a line.
• The slope is denoted by 𝒎.

Gradient between two points
●The gradient between two points is determined by the ratio of vertical
change to horizontal change.
●The formula for finding the gradient of a line is:

• If line rises from left to right, 𝒎 > 𝒐
• If line goes from right to left, 𝒎 < 𝟎
• If line is parallel to x-axis, 𝒎 = 𝟎
•If line is parallel to y-axis, 𝒎 = 𝒖𝒏𝒅𝒆𝒇𝒊𝒏𝒆𝒅
SLOPE OF A LINE

• Two non-vertical lines are parallel if, and only if, their
slopes are equal.
• Two slant lines are perpendicular if, and only if, the slope
of one is the negative reciprocal of the slope of the
other..(If two lines are perpendicular, the product of their
gradients is equal to −1.)
• For horizontal lines the gradient is equal to 0.
• For vertical lines the gradient is undefined.

If 2 lines with gradients m1 and m2 are perpendicular then m1 × m2 = -1
Conversely:
If m1 × m2 = -1 then the two lines with gradients m1 and m2 are perpendicular.

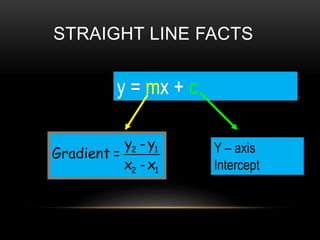
STRAIGHT LINE FACTS
Y – axis
Intercept
2 1
2 1
y - y
Gradient =
x -x
y = mx + c

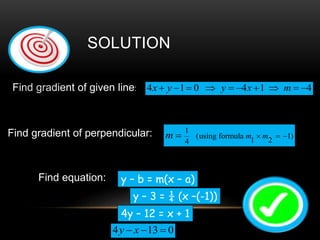
Find the equation of the line which passes
through the point (-1, 3) and is perpendicular to
the line with equation 4 1 0x y  

Find gradient of given line: 4 1 0 4 1 4x y y x m         
Find gradient of perpendicular: 1
(using formula 1)
1 24
   m mm
Find equation:
4 13 0y x  
SOLUTION
y – b = m(x – a)
y – 3 = ¼ (x –(-1))
4y – 12 = x + 1

This presentation is a mash up of 6 different sources. These are:
Felipe, N, M. (2014). Analytical geometry basic concepts [PowerPoint
Presentation]. Available at: http://www.slideshare.net/NancyFelipe1/analytic-
geometry-basic-concepts. Accessed on: 6 March 2014.
Demirdag, D. (2013). Lecture #4 analytic geometry [PowerPoint
Presentation]. Available at:
http://www.slideshare.net/denmarmarasigan/lecture-4-analytic-geometry.
Accessed on: 6 March 2014.
Share, S. (2014). Analytical geometry [PowerPoint Presentation]. Available
at: http://www.slideshare.net/SuziShare/analytical-geometry. Accessed on: 6
March 2014.
Derirdag, D. (2012).Analytical geometry [PowerPoint Presentation]. Available
at: http://www.slideshare.net/mstfdemirdag/analytic-geometry. Accessed on:
6 March 2014.
Nolasco, C, M. Analytical geometry [PowerPoint Presentation]. Available at:
http://www.slideshare.net/CecilleMaeNolasco/analytical-geometry. Accessed
on: 6 March 2014.
Siyavula_Education. (2012).Analytical geometry Everything Maths, Grade
10 [PowerPoint Presentation}. Available at:
http://www.slideshare.net/Siyavula_Education/analytical-
geometry?qid=9526d5d1-098f-45da-90b6-
d503de7f2db5&v=default&b=&from_search=4). Accessed on: 6 March 2014.

�ݺ�ߣ

Grade 10 analytical geometry

More Related Content

Grade 10 analytical geometry