GRADE 5 SESSION 6.pptx
- 1. MTAP Program of Excellence in Mathematics Grade 5 Session 6 Name of Facilitator
- 2. POLYGONS
- 3. A. Tell whether the following figure is a polygon or not. P 1. 2. 3. 4. 5. NP P P NP P NP NP NP P 6. 7. 8. 9. 10.
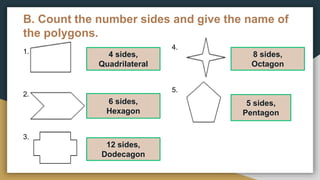
- 4. B. Count the number sides and give the name of the polygons. 1. 2. 3. 4. 5. 4 sides, Quadrilateral 6 sides, Hexagon 12 sides, Dodecagon 8 sides, Octagon 5 sides, Pentagon
- 5. C. Complete the table below. NAME OF THE POLYGON NO. OF SIDES 1. Quadrilateral 2. 3 3. 8 4. Decagon 5. Dodecagon 6. 9 7. Hexagon 8. Heptagon 9. 20 10. Hectagon 4 Triangle Octagon 10 12 Nonagon Icosagon 6 7 100
- 6. D. Tell whether the following is TRUE or FALSE. 1. The sides of a simple polygon do not intersect and meet only at their endpoints. 2. Complex polygons have sides which also do not intersect. 3. Concave polygon is a polygon that has an angle that measures more than 180 degrees. 4. Polygons that are having the same size and shape are called similar polygons. 5. Two polygons that are having the same shape but not necessarily the same size are said to be congruent. TRUE FALSE TRUE FALSE FALSE
- 7. D. Tell whether the following is TRUE or FALSE. 6. All sides and angles of a regular polygon are congruent. 7. A rhombus is a regular polygon. 8. A square is an irregular polygon. 9. All squares are rectangle but not all rectangles are squares. 10. Concave polygon is a polygon that has an angle that measures more than 180 degrees. A circle is a closed plane figure and is the set of all points equidistant from a fixed point called center. TRUE FALSE FALSE TRUE TRUE
- 8. E. Given the figure at the right, name the following: 1. A diameter 2. A chord 3. Radii 4. Center 5. Points on the circle ?? or ?? ?? or ?? , ?? or ?? ?? or ?? , ?? or ?? , ?? or ?? O A, B, C , D
- 9. F. i. Give the radius of the following of its diameter is: 1. 12 cm 2. 7 cm 3. 8 ? cm 4. 288 mm 5. 16.88 in 6 cm 3.5 cm 4 1/4 cm 144 mm 8.44 in REMEMBER: Radius = ? (Diameter)
- 10. F. ii. Give the diameter of the following of its radius is: 1. 10 cm 2. 9 cm 3. 10.5 in 4. 10 ? dm 5. 6.33 m 20 cm 18 cm 21 in 21 ? dm 12.66 m REMEMBER: Diameter = 2(Radius)
- 11. MEASUREMENTS .
- 12. G. Convert the following measure to its desired units. 1. 20 cm = ______ cm 6 . 5 m2 = _______ cm2 2. 12 cm = ______ cm 7. 10 m2 = ________ cm2 3. 12.34 cm = _______ m 8. 8, 000, 000 cm2 = ______ m2 4. 8, 590 cm = ______ m 9. 5, 500 cm2 = ______ m2 5. 96.35 m = ______ cm 10. 16.05 m2 = _________ cm2 2000 1200 0.1234 85.9 9 635 50 000 100 000 800 0.55 160 500
- 13. H. Convert the following measure to its desired units. 1. 4 m3 = ____________ cm3 6 . 6 L m2 = ________ cm3 2. 0.7 m3 = __________ cm3 7. 1, 500 L m2 = _______ m3 3. 3, 000, 000 cm = ______ m3 8. 250 Lcm2 = _______ m3 4. 700, 000 cm = ________ m3 9. 2, 000, 000 cm3 = ______ L 5. 2.5 L = ________ cm3 10. 28 m3 = _______ L 4, 000,000 700, 000 3 7 2 500 6000 1.5 0.25 2000 28 000
- 15. I. Answer each of the following problems: 1. Find the perimeter and area of a square of side: a. 11 m b. 23 dm c. 45 cm Answer: a. s = 11 m : P = 4 x 11 = 44 m ; A = 11 x 11 = 121 m2. b. s = 23 dm : P = 4 x 23 = 92 dm ; A = 23 x 23 = 529 dm2 c. s = 45 cm : P = 4 x 45 = 180 cm ; A = 45 x 45 = 2025 cm2
- 16. 2. Find the perimeter and area of a rectangle if: a. L = 18 cm, W = 12 cm b. L = 2.5 m, W = 3.8 m Answer: a. L = 18 cm, W = 12 cm : P = 2(18 + 12) = 60 cm ; A = 18 x 12 = 216 cm2 b. L = 2.5 m, W = 3.8 m : P = 2 (2.5 + 3.8) = 12.6 m; A = 2.5 x 3.8 = 9.5 m2
- 17. 3. Vince wants to put a ribbon around the circular can of biscuits. If the can has a radius of 24 cm, find the circumference of the can. Answer: r = 24 cm , C = 2”ąr , then C = 2(3.14)(24) = 150.72 cm. Therefore, the circumference is 150.72 cm
- 18. 4. Zoie wants to sew lace along the edges of her 5 placemats. If a placemat is 13 cm long and 9 cm wide, how many meters of lace does she need? Answer: l = 13 cm, w = 9 cm ; P = 2(13+9) = 44 cm lace needed for one placemat, since Zoie has 5 placemats, so 5(44cm) = 220 cm. The total length of lace needed in meters is 2.2.
- 19. 5. JohnĪ»s father built a wading pool for him that is 2.5 meters by 3.5 meters. If John walks around the pool 7 times, how many meters will that be? Answer: l = 2.5 m, w=3.5 m ; P = 2(2.5+3.5)m = 12 m. If John walks around 7 times, then that would be 7 x 12 = 84 m.
- 20. 6. Jhumar wants to tie a rope around a post that has a circular cross section of 1.5 m. What is the circumference around it? Answer: d = 1.5 m ; C = 2”ąr, then C = 2(3.14)(1.5) = 9.42 m. Then the circumference of the post is 9.42 m.
- 21. 7. The distance around the circular field is 471meters. a. Find the diameter of the circular field. b. What is the area of the circular field? The distance around the circular field is 471 meters. a. C = ”ąd, 471 = (3.14)(d), 471Ī┬3.14 = d, d = 150 m Answer: b. d = 150 m, so r = 75 m; A = ”ąr2 , then A = (3.14)(75m)2 = 17, 662.5 m2
- 22. 8. A rectangular prism has a height of 3 in, width of 3 in and length of 8 in. Find the volume of the rectangular prism. Answer: l = 8 in, w = 3 in, and h = 3 in :V = lwh , then V = 8(3)(3)in3 = 72 in3. Therefore, the volume of the rectangular prism is 72 in3
- 23. 9. A square tile of side 25cm costs ?30.50. How much would it cost to tile the floor of a bathroom that is 5 m in length and 3 m in width? If the tiles are squares of side 25 cm, the 5 m side needs 500/25 = 20 tiles and the 3 m side needs 300 cm/25 cm = 12 tiles. The bathroom needs 20 rows of 12 times or 240 tiles in all. At ?30.50 a tile, it will cost 240 x ?30.50 = ?7 320.00 for the cost of the tiles. Answer:
- 24. 10. A can of sardines has a radius of 10 cm and a height of 8 cm. A can of pineapple juice has a radius of 8 cm and a height of 10 cm. Which cylinder has a greater volume? V of the sardines is 3.14(10 x 10)(8) cm3 = 2 512 cm3 , while the V of the can of pineapple juice is 3.14(8 x 8)10 cm3 = 2 000.6 cm3. Therefore, the can of sardines has a greater volume. Answer:
- 25. CHALLENGE!
- 26. Let us apply what we learned!
- 27. Solve the following problems. 1. Sean is going to paint a circle on a piece of cardboard. The area of the circle is 706.5 square centimeters. What is the radius of the circle? 1. A of the circle is 706.5 cm2, therefore 706.5 cm2 = 3.14r2, so 225 cm2 = r2, Ī╠225 = r. Therefore r = 15 cm.
- 28. 2. The circumference of a circular clock is 244.92 dm. What is the diameter of the clock? Find the area of the clock. The circumference of a circular clock is 244.92 dm. a. What is the diameter of the clock? C = ”ąd, 244.92 = (3.14)d, then 244.92Ī┬3.14 = d , so d= 78 dm. b. Find the area of the clock. A = ”ąr2, since d = 78 dm, so r= 39 dm, computing for the area A = (3.14)(39)2, therefore A = 4 775.94 dm2
- 29. 3. Three cans have capacities of three, five and nine liters. How can you use the cans to measure exactly 7 liters of water? Three cans have capacities of 3 L, 5 L and 9 L. To get 7 L of water using the three cans, water has to go from one can to another as shown. The numbers show ©C begin with 9 L of water in the 9 L can. Then fill the 3 L can and 5 L can. Next place the content of the 3 L can into the 9 L can. Then, fill the 3 L can from the 5 L can. Finally, empty the 3 L can into the 9 L can, to have 7 liters of water in it.
- 30. 4. To fence the side of his property facing a street, Mr. Cruz planned to use fence posts 2 meters apart. Because of the increase in the price of the posts, he decided to buy 4 fewer posts and place them 3 meters apart. How many posts would he have bought at first? Let x be the number of posts he would have bought at first to be placed 2 m apart. That gives x -1, 2 m spaces and the space to be fenced 2(x-1) m. If there are 4 fewer posts, that means x ©C 5 spaces 3 m apart and 2(x ©C 1) m = 3(x ©C 5) m. Solving gives 2(x -1)m = 3(x ©C 5) m. 2x ©C 2 = 3x ©C 15. x = 13 posts to be bought at first to fence 12 x 2 m = 24 m. Buying 4 posts fewer means buying only 9 and the same space 3 x 8 = 24 m can be fenced.
- 31. 5. A swimming pool that is 25 m by 15 m has a 2 m concrete walk built around it. What is the area of the pool and walk? What is the area of the walk? The swimming pool has an area of 25 x 15 = 375 sq. m. The area of the pool and concrete walk is 29 x 19 sq.m. = 551 sq. m. Area of walk = (551 ©C 375) sq.m. = 176 sq.m. m 2 ? m 25 m 27
- 32. 6. If one box is 1 cubic centimeter, what is the volume of this figure? If one box is 1 cubic centimeter, then; V of the figure = V1 + V2 + V3 + V4 + V5 = 16 cm3 + 12 cm3 + 8 cm3 + 4 cm3 + 2cm3 = 42 cm3