Grade-7-C-Set Operatios and Venn Diagrams.pptx
- 1. Welcome to your Mathematics Class Grade 7 Teacher: Mrs. Susan b. Palacio
- 2. Dear Lord and Father of all, ✗ Thank you for today. ✗ Thank you for ways in which you provide for us all. ✗ For Your protection and love we thank you. Help us to focus our hearts and minds now on what we are about to learn. ✗ Inspire us by Your Holy Spirit as we listen and write. ✗ Guide us by your eternal light as we discover more about the world around us. ✗ We ask all this in the name of Jesus. ✗ Amen. 2
- 3. 1.Be on time. 2.Always turn on your camera. 3.Unmute your audio when called by your teacher. 3 4.Do have your module, notebook and pen. 5.Questions will be entertained after a discussed topic. 6.Be attentive and enjoy learning.
- 4. ATTENDANCE 1
- 5. MATH 7- QUARTER 1 - DAY 3 set OPERATIONS 5
- 6. Looking Back at your Lesson ✗ From the previous module, you have learned that a set is a well- defined group of objects, called elements, which share a common characteristic. The different set operations are: ✗ 1. Union of Sets: The union of the sets A and B, denoted by A∪B, is the set that contains those elements that belong to A, B, or to both. ✗ 2. Intersection of Sets: The intersection of the sets A and B, denoted by A∩B, is the set containing those elements that belong to both A and B. 6
- 7. Looking Back at your Lesson ✗ From the previous module, you have learned that a set is a well- defined group of objects, called elements, which share a common characteristic. The different set operations are: ✗ 3. Complement of a Set: The complement of a set A, written as A’, is the set of all elements found in the universal set, U, that are not found in set A. ✗ 4. Difference of Sets: The difference of two sets, written as A – B, is the set of all elements of A that are not elements of B. 7
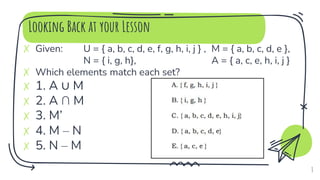
- 8. Looking Back at your Lesson ✗ Given: U = { a, b, c, d, e, f, g, h, i, j } , M = { a, b, c, d, e }, N = { i, g, h}, A = { a, c, e, h, i, j } ✗ Which elements match each set? ✗ 1. A ∪ M ✗ 2. A ∩ M ✗ 3. M’ ✗ 4. M – N ✗ 5. N – M 8
- 10. Venn Diagram Defined A Venn Diagram refers to the diagram that shows the relationship between and among sets of objects. It was first introduced by the mathematician John Venn in 1880s. This diagram enables you to organize information visually so that you can see the relationships between two or three sets of items. You can then identify similarities and differences. You can also determine what elements are in a set and what elements do not belong to the set. A Venn diagram consists of two or more overlapping closed curves, usually circles, each representing a set. 10
- 11. Visualizing the different regions in a Venn diagram The idea of the Venn Diagram is simple: sets are shown as regions. The inside of the circle represents elements of a set, the outside contains anything that is not in that set. Shown on the right is an example of a Venn Diagram. By convention, capital letters are used to denote sets. If you happen to see small letters, consider these small letters as elements. Braces,{ }, denote a list of elements in a set. 11
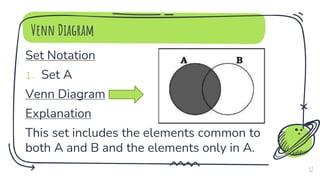
- 12. Venn Diagram Set Notation 1. Set A Venn Diagram Explanation This set includes the elements common to both A and B and the elements only in A. 12
- 13. Venn Diagram Set Notation 2. Set B Venn Diagram Explanation This set includes the elements common to both A and B and the elements only in B. 13
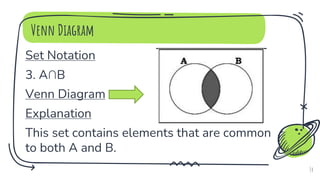
- 14. Venn Diagram Set Notation 3. A∩B Venn Diagram Explanation This set contains elements that are common to both A and B. 14
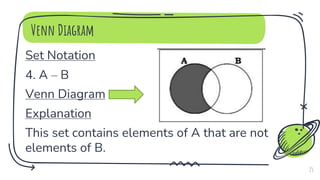
- 15. Venn Diagram Set Notation 4. A – B Venn Diagram Explanation This set contains elements of A that are not elements of B. 15
- 16. Venn Diagram Set Notation 5. B – A Venn Diagram Explanation This set contains elements of B that are not elements of A. 16
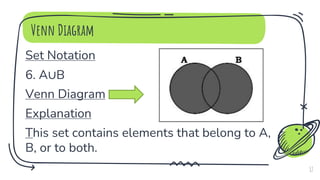
- 17. Venn Diagram Set Notation 6. A∪B Venn Diagram Explanation This set contains elements that belong to A, B, or to both. 17
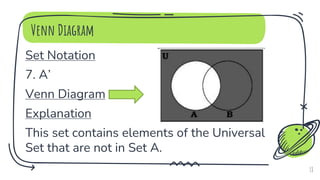
- 18. Venn Diagram Set Notation 7. A’ Venn Diagram Explanation This set contains elements of the Universal Set that are not in Set A. 18
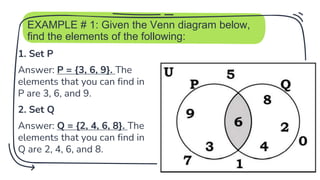
- 19. EXAMPLE # 1: Given the Venn diagram below, find the elements of the following: 1. Set P Answer: P = {3, 6, 9}. The elements that you can find in P are 3, 6, and 9. 2. Set Q Answer: Q = {2, 4, 6, 8}. The elements that you can find in Q are 2, 4, 6, and 8. 19
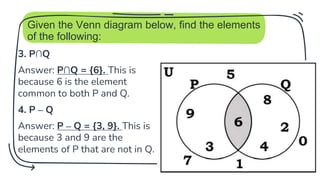
- 20. Given the Venn diagram below, find the elements of the following: 3. P∩Q Answer: P∩Q = {6}. This is because 6 is the element common to both P and Q. 4. P – Q Answer: P – Q = {3, 9}. This is because 3 and 9 are the elements of P that are not in Q. 20
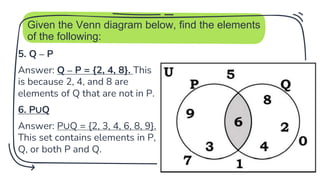
- 21. Given the Venn diagram below, find the elements of the following: 5. Q – P Answer: Q – P = {2, 4, 8}. This is because 2, 4, and 8 are elements of Q that are not in P. 6. P∪Q Answer: P∪Q = {2, 3, 4, 6, 8, 9}. This set contains elements in P, Q, or both P and Q. 21
- 22. Given the Venn diagram below, find the elements of the following: 7. P’ Answer: P’ = {0, 1, 2, 4, 5, 7, 8}. This set contains elements of the universal set which are not in P. 22
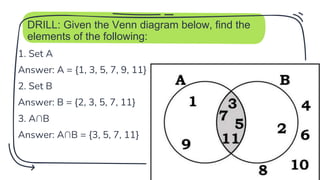
- 23. DRILL: Given the Venn diagram below, find the elements of the following: 1. Set A Answer: A = {1, 3, 5, 7, 9, 11} 2. Set B Answer: B = {2, 3, 5, 7, 11} 3. A∩B Answer: A∩B = {3, 5, 7, 11} 23
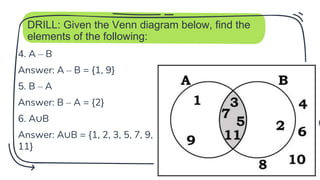
- 24. DRILL: Given the Venn diagram below, find the elements of the following: 4. A – B Answer: A – B = {1, 9} 5. B – A Answer: B – A = {2} 6. A∪B Answer: A∪B = {1, 2, 3, 5, 7, 9, 11} 24
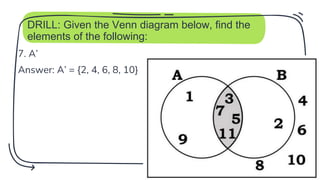
- 25. DRILL: Given the Venn diagram below, find the elements of the following: 7. A’ Answer: A’ = {2, 4, 6, 8, 10} 25
- 26. 26